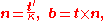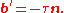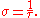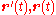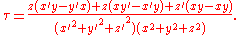Torsion of curves
Encyclopedia
In the elementary differential geometry of curves
in three dimensions, the torsion of a curve
measures how sharply it is twisting. Taken together,
the curvature
and the torsion of a space curve are analogous to the curvature
of a plane curve. For example, they are coefficients in the system of differential equation
s for the Frenet frame given by the Frenet–Serret formulas.
of C at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors
where the prime denotes the derivative of the vector with respect to the parameter. The torsion
measures the speed of rotation of the binormal vector at the given point. It is found from the equation
which means
Remark: The derivative of the binormal vector is perpendicular to both the binormal and the tangent, hence it has to be proportional to the principal normal vector. The negative sign is simply a matter of convention: it is a by-product of the historical development of the subject.
The radius of torsion, often denoted by σ, is defined as
of a space curve. Assume that this is a regular parametrization and that the curvature
of the curve does not vanish. Analytically, r(t) is a three times differentiable function
of t with values in R3 and the vectors
are linearly independent.
Then the torsion can be computed from the following formula:
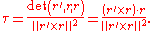
Here the primes denote the derivative
s with respect to t and the cross denotes the cross product
. For r = (x, y, z), the formula in components is
Differential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
in three dimensions, the torsion of a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
measures how sharply it is twisting. Taken together,
the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
and the torsion of a space curve are analogous to the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of a plane curve. For example, they are coefficients in the system of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s for the Frenet frame given by the Frenet–Serret formulas.
Definition
Let C be a space curve in a unit-length (or natural) parametrization and with the unit tangent vector t. If the curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of C at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors
where the prime denotes the derivative of the vector with respect to the parameter. The torsion
measures the speed of rotation of the binormal vector at the given point. It is found from the equation
which means
Remark: The derivative of the binormal vector is perpendicular to both the binormal and the tangent, hence it has to be proportional to the principal normal vector. The negative sign is simply a matter of convention: it is a by-product of the historical development of the subject.
The radius of torsion, often denoted by σ, is defined as
Properties
- A plane curve with non-vanishing curvature has zero torsion at all points. Conversely, if the torsion of a regular curve with non-vanishing curvature is identically zero, then this curve belongs to a fixed plane.
- The curvature and the torsion of a helixHelixA helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
are constant. Conversely, any space curve with constant non-zero curvature and constant torsion is a helix. The torsion is positive for a right-handed helix and is negative for a left-handed one.
Alternative description
Let r = r(t) be the parametric equationParametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
of a space curve. Assume that this is a regular parametrization and that the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the curve does not vanish. Analytically, r(t) is a three times differentiable function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of t with values in R3 and the vectors
are linearly independent.
Then the torsion can be computed from the following formula:
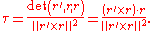
Here the primes denote the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s with respect to t and the cross denotes the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
. For r = (x, y, z), the formula in components is
