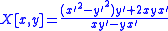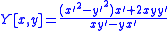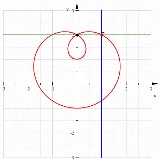
In the plane, for every point X other than P there is a unique line through X perpendicular to XP. For a given curve in the plane and a given fixed point P, called the pedal point, the negative pedal curve is the envelope

Envelope (mathematics)

In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...

 of the lines XP for which X lies on the given curve.

The negative pedal curve of a pedal curve

Pedal curve

In the differential geometry of curves, a pedal curve is a curve derived by construction from a given curve ....

with the same pedal point is the original curve.

For a parametrically defined curve, its negative pedal curve with pedal point (0; 0) is defined as

External links

• Negative pedal curve on Mathworld