Jürgen Ehlers
Encyclopedia
Jürgen Ehlers was a German
physicist
who made notable contributions to the current understanding of Albert Einstein
's theory of general relativity
. From graduate and postgraduate work in Pascual Jordan
's relativity group at Hamburg University, he moved on to various lecturer- and professorships before joining the Max Planck Institute for Astrophysics
in Munich
as a director. In 1995, he became the founding director of the newly created Max Planck Institute for Gravitational Physics (Albert Einstein Institute) in Potsdam
, Germany
.
Ehlers' research focused on the foundations of general relativity
, as well as its applications to various areas astrophysics
. In particular, he is notable for his work on the classification of exact solution
s to Einstein's field equations, for the Ehlers-Geren-Sachs theorem
that justifies the application of simple, general-relativistic model universes to modern cosmology
, for a spacetime
-oriented description of gravitational lensing, and for his work on the relationship between models formulated within the framework of general relativity and those of Newtonian gravity. In addition, Ehlers had a keen interest in both the history and philosophy of physics, and was an ardent popularizer of science.
. He attended public schools from 1936 to 1949, and went on to study physics, mathematics, and philosophy at Hamburg University from 1949 to 1955. In the winter term of 1955/56, he passed the high school teacher's examen, but went on to graduate research in the group of Pascual Jordan
, with Jordan acting as his thesis advisor. His work on the construction and characterization of solution
s of the Einstein field equations
earned him a doctorate in 1958. While earlier, the main research of Jordan's group had been dedicated to a scalar-tensor modification of Einstein's theory of general relativity
, now known as Jordan-Brans-Dicke theory, in which the gravitational constant
is variable, Ehlers was instrumental in changing the group's focus to the structure and interpretation of Einstein's original theory. Other members of the group included Wolfgang Kundt, Engelbert Schücking
, Otto Heckmann
, Rainer Sachs, and Manfred Trümper.
In 1961, having become Jordan's assistant, Ehlers obtained his habilitation
, the advanced degree that, by the rules of German academia, qualifies the bearer for a professorship. He then held teaching and research positions at the University of Kiel
, Syracuse University
, and Hamburg University, before once more moving to the United States: from 1964 to 1965, he was at the Graduate Research Center of the Southwest in Dallas, and from 1965 to 1971 at the University of Texas in Austin, joining Alfred Schild
's group first as an associate professor and, from 1967 on, as a full professor of physics. During that time, he also held visiting professorships at the universities of Würzburg
and Bonn
.
in Munich
, one of the institutes of Germany's major organization for basic research, the Max Planck Society
, as the director of its gravitational theory department. Ehlers' name had been brought into play by Ludwig Biermann
, the institute's director at the time. When he joined the institute in 1971, Ehlers also became an adjunct professor at Munich's Ludwig Maximilian University. In March 1991, the institute was split into the Max Planck Institute for Physics
and the Max Planck Institute for Astrophysics
, where Ehlers' department found a new home. Over the 24 years of his tenure, his research group was home to, among others, Gary Gibbons
, John Stewart and Bernd Schmidt, as well as visiting scientists including Abhay Ashtekar
, Demetrios Christodoulou
, and Brandon Carter
.
One of Ehlers' post-docs in Munich was Reinhard Breuer, who would later go on to become the editor-in-chief of Spektrum der Wissenschaft, the German
edition of the popular-science journal Scientific American
.
dedicated to research on Einstein's theories of gravity. He was successful, and on June 9, 1994, the Max Planck Society officially decided to found the Max Planck Institute for Gravitational Physics
in Potsdam
. Ehlers became its founding director, as well as the leader of its department for the foundations and mathematics of general relativity, when the institute started operating on April 1, 1995. He also oversaw the founding of a second institute department devoted to gravitational wave
research and headed by Bernard F. Schutz
. On December 31, 1998, Ehlers retired to become founding director emeritus. He continued to work at the institute until his death on May 20, 2008.
(1972), the Leopoldina in Halle
(1975), and the Bavarian Academy of Sciences and Humanities in Munich
(1979). From 1995 to 1998, he served as president of the International Society on General Relativity and Gravitation
. He also received the 2002 Max Planck Medal
of the German Physical Society
, the Volta
Gold Medal of Pavia University (2005), and the medal of the Faculty of Natural Sciences of Charles University, Prague
(2007).
. In particular, he made important contributions to cosmology
, the theory of gravitational lens
es and gravitational waves. His principal concern was to clarify the theory's mathematical structure and its consequences, separating rigorous proofs from heuristic conjectures.
s of Einstein's equations – in effect, universes consistent with the laws of general relativity which are simple enough to allow for an explicit description in terms of basic mathematical expressions – play a key role when it comes to building general-relativistic models. However, general relativity is a fully covariant theory – its laws are the same, independent of which coordinates are chosen to describe a given situation. One direct consequence is that two apparently different exact solution
s to Einstein's equations could, in fact, correspond the same model universe, and differ only in the coordinates used in their description. Ehlers began to look for serviceable ways of characterizing exact solutions invariantly, that is, in ways that do not depend on the choice of coordinates. To this end, he examined ways of describing the intrinsic geometric properties of the known exact solutions.
During the 1960s, following up on the groundwork of research for his doctoral thesis, Ehlers published a series of seminal papers, all but one in collaboration with colleagues from the Hamburg group. The first, written with Jordan and Wolfgang Kundt, is a systematic exposition of the properties and characteristics of exact solution
s to Einstein's field equations, using tools from differential geometry such as the Petrov classification
of Weyl tensor
s (that is, those parts of the Riemann tensor describing the curvature
of space-time which are not constrained by Einstein's equations), isometry
groups
, and conformal
transformations. This work also includes the first definition of pp-waves, a class of especially simple gravitational wave
s, as well as their classification. There were also two treatises on gravitational radiation (one with Rainer Sachs, one with Manfred Trümper). The work with Sachs studies, among other things, vacuum solutions with special algebra
ic properties, using the 2-component spinor
formalism. It also gives a systematic exposition of the geometric properties of bundles (congruences) of light beams in terms of their expansion (simply put, how the beams converge or diverge), twist and shear (how, apart from growing or shrinking, the cross section is deformed). One of the results is the Ehlers-Sachs theorem describing the properties of the shadow produced by a narrow beam of light passing an opaque object. The tools developed in that work would prove to be essential for the discovery by Roy Kerr
of the Kerr solution, describing a rotating black hole
– arguably the most important exact solution of all. The last of these seminal papers dealt with the general-relativistic treatment of the mechanics of continuous media.
Another part of Ehlers' exploration of exact solutions in his thesis led to a result that would later prove to be important. At the time Ehlers started his research on his doctoral thesis, the Golden age of general relativity
had not quite begun, and the basic properties and concepts of black holes were not yet understood. In the work that led to his doctoral thesis, Ehlers proved important properties of the surface around a black hole that would later be identified as its horizon
, in particular that the gravitational field inside cannot be static, but must change with time.
vacuum
spacetime
, which maps solutions of Einstein's field equations to other solutions. This symmetry between the tt-component of the metric and a term known as the twist potential is analogous to the duality between the electric field
E and the magnetic field
field B in source-free electrodynamics, where the replacement E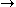
–B, B 
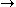E leaves Maxwell's equations
invariant. This duality was later generalized to an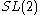
symmetry which became known as the Ehlers group
. Further generalizations led to the discovery of the infinite-dimensional Geroch group
(the Geroch group is generated by two non-commuting
subgroup
s, one of which is the Ehlers group). These so-called hidden symmetries play an important role in the Kaluza-Klein reduction of both general relativity and its generalizations, such as eleven-dimensional supergravity
. Other applications include their use as a tool in the discovery of previously unknown solutions, and their role in a proof that solutions in the stationary axi-symmetric case form an integrable system
.
, published in 1968 by Ehlers, P. Geren and Rainer Sachs, shows that if, in a given universe, all freely falling observers measure the cosmic background radiation to have exactly the same properties in all directions (that is, they measure the background radiation to be isotropic), then that universe is an isotropic and homogeneous FLRW spacetime.
on a constructive-axiomatic approach to general relativity: a way of deriving Einstein's theory from a minimal set of elementary objects and axioms specifying their properties. The basic ingredients of their approach are primitive concepts such as event
, light
ray, particle
, and freely falling particle
. At the outset, spacetime is a mere set of events, without any further structure. By postulating the basic properties of light and freely falling particles as axioms, the differential topology
, conformal structure and, finally, the metric
structure of spacetime are constructed; key steps of the construction correspond to idealized measurements, such the standard range finding used in radar
. As the final step, Einstein's equations are derived from the weakest possible set of additional axioms. The result is a formulation in which the assumptions underlying general relativity are clearly identified.
In the 1970s, in collaboration with Ekkart Rudolph, Ehlers addressed the problem of rigid bodies in general relativity. Rigid bodies are a fundamental concept in classical physics, but the fact that their different parts by definition move simultaneously is incompatible with the relativistic concept of the speed of light
as a limiting speed for the propagation of signals and other influences. As early as 1909, Max Born
had given a definition of rigidity that was compatible with relativistic physics. However, this definition depends on certain assumptions that are not satisfied in a general space-time, and are also overly restrictive. Ehlers and Rudolph generalized Born's definition to a more readily applicable definition they called "pseudo-rigidity", which represents a more satisfactory approximation to the rigidity of classical physics.
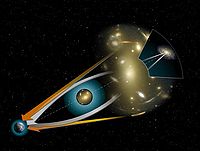With Peter Schneider, Ehlers embarked on an in-depth study of the foundations of gravitational lensing. One result of this work was an 1992 monograph co-authored with both Schneider and Emilio Falco: the first systematic exposition of the field that included both the theoretical foundations and observational results. From the viewpoint of astronomy, gravitational lensing is often described using a quasi-Newtonian approximation — assuming the gravitational field
to be small and the deflection angles to be minute — which is perfectly sufficient for most situations of astrophysical relevance. In contrast, the monograph developed a thorough and complete description of gravitational lensing from a fully relativistic space-time perspective. This feature of the book has played a major part in the book's long-term positive reception. In the following years, Ehlers continued his research on the propagation of bundles of light in arbitrary spacetimes.
. Later work by Élie Cartan
, Kurt Friedrichs and others showed more concretely how a geometrical generalization of Newton's theory of gravity known as Newton-Cartan theory
could be understood as a (degenerate) limit of general relativity
, obtained by letting a specific parameter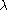
go to zero. Ehlers extended this work by developing a frame theory, a mathematically precise way of constructing the Newton-Cartan limit not only of the physical laws of general relativity, but of any spacetime obeying those laws, that is, of any solution to Einstein's equations. For instance, this can be used to show that the Newtonian limit of a Schwarzschild black hole is a simple point particle
; in addition, Newtonian versions of interesting exact solutions such as the Friedman-Lemaître models or the Gödel universe can be constructed.
Ehlers also took part in the discussion of how the back-reaction
from gravitational radiation onto a radiating system could be systematically described in a non-linear theory such as general relativity, pointing out that the standard quadrupole
formula for the energy flux for systems like the binary pulsar
had not yet been rigorously derived: A priori, a derivation demanded the inclusion of higher-order terms than was commonly assumed, and in fact higher terms than were computed until then.
His work on the Newtonian limit, in particular in relation to cosmological
solutions, also led Ehlers, together with his former doctoral student Thomas Buchert, to a systematic study of perturbations and inhomogeneities in a Newtonian cosmos. This laid the groundwork for Buchert's later general-relativistic generalization of this treatment of inhomogeneities, the basis of his attempt to explain what is currently seen as the cosmic effects of a cosmological constant
or, in modern parlance, dark energy
, as a non-linear consequence of inhomogeneities in general-relativistic cosmology.
in Berlin. In particular, he explored Pascual Jordan's seminal contributions to the development of quantum field theory
between 1925 and 1928. Throughout his career, Ehlers had an interest in the philosophical foundations and implications of physics, and contributed to research on this topic by addressing questions such as the basic status of scientific knowledge in physics.
in Berlin
. He is the author of a number of popular-science articles, including contributions to general-audience journals such as Bild der Wissenschaft. and also edited a compilation of articles on gravity from the German edition of Scientific American
.
Ehlers also directly addressed physics teachers, be it in talks or in journal articles on the teaching of relativity and related basic ideas of physics, such as on mathematics
as the language of physics.
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
who made notable contributions to the current understanding of Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. From graduate and postgraduate work in Pascual Jordan
Pascual Jordan
-Further reading:...
's relativity group at Hamburg University, he moved on to various lecturer- and professorships before joining the Max Planck Institute for Astrophysics
Max Planck Institute for Astrophysics
The Max Planck Institute for Astrophysics is a Max Planck Institute, located in Garching, near Munich, Bavaria, Germany. It was founded as Max Planck Institute for Physics and Astrophysics in 1958 and split up into the Max Planck Institute for Astrophysics and the Max Planck Institute for Physics...
in Munich
Munich
Munich The city's motto is "" . Before 2006, it was "Weltstadt mit Herz" . Its native name, , is derived from the Old High German Munichen, meaning "by the monks' place". The city's name derives from the monks of the Benedictine order who founded the city; hence the monk depicted on the city's coat...
as a director. In 1995, he became the founding director of the newly created Max Planck Institute for Gravitational Physics (Albert Einstein Institute) in Potsdam
Potsdam
Potsdam is the capital city of the German federal state of Brandenburg and part of the Berlin/Brandenburg Metropolitan Region. It is situated on the River Havel, southwest of Berlin city centre....
, Germany
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
.
Ehlers' research focused on the foundations of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, as well as its applications to various areas astrophysics
Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
. In particular, he is notable for his work on the classification of exact solution
Exact solution
In mathematics and especially physics, an exact solution is a solution to a problem that encapsulates the whole mathematics or physics of the problem without using an approximation.-References:*...
s to Einstein's field equations, for the Ehlers-Geren-Sachs theorem
Ehlers-Geren-Sachs theorem
The Ehlers-Geren-Sachs theorem, published in 1968 by Jürgen Ehlers, P. Geren and Rainer Sachs, shows that if, in a given universe, all freely falling observers measure the cosmic background radiation to have exactly the same properties in all directions , then that universe is an isotropic and...
that justifies the application of simple, general-relativistic model universes to modern cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
, for a spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
-oriented description of gravitational lensing, and for his work on the relationship between models formulated within the framework of general relativity and those of Newtonian gravity. In addition, Ehlers had a keen interest in both the history and philosophy of physics, and was an ardent popularizer of science.
Early career
Jürgen Ehlers was born in HamburgHamburg
-History:The first historic name for the city was, according to Claudius Ptolemy's reports, Treva.But the city takes its modern name, Hamburg, from the first permanent building on the site, a castle whose construction was ordered by the Emperor Charlemagne in AD 808...
. He attended public schools from 1936 to 1949, and went on to study physics, mathematics, and philosophy at Hamburg University from 1949 to 1955. In the winter term of 1955/56, he passed the high school teacher's examen, but went on to graduate research in the group of Pascual Jordan
Pascual Jordan
-Further reading:...
, with Jordan acting as his thesis advisor. His work on the construction and characterization of solution
Solution
In chemistry, a solution is a homogeneous mixture composed of only one phase. In such a mixture, a solute is dissolved in another substance, known as a solvent. The solvent does the dissolving.- Types of solutions :...
s of the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
earned him a doctorate in 1958. While earlier, the main research of Jordan's group had been dedicated to a scalar-tensor modification of Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, now known as Jordan-Brans-Dicke theory, in which the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
is variable, Ehlers was instrumental in changing the group's focus to the structure and interpretation of Einstein's original theory. Other members of the group included Wolfgang Kundt, Engelbert Schücking
Engelbert Schücking
Engelbert Schücking is a physics professor at New York University in New York City. His research interests are theoretical astrophysics, general relativity and cosmology...
, Otto Heckmann
Otto Heckmann
Otto Hermann Leopold Heckmann was a German astronomer.He directed the Hamburg Observatory from 1941 to 1962, after which he became the first director of the European Southern Observatory. , Otto Heckmann He actively contributed to the creation of the third issue of the Astronomische Gesellschaft...
, Rainer Sachs, and Manfred Trümper.
In 1961, having become Jordan's assistant, Ehlers obtained his habilitation
Habilitation
Habilitation is the highest academic qualification a scholar can achieve by his or her own pursuit in several European and Asian countries. Earned after obtaining a research doctorate, such as a PhD, habilitation requires the candidate to write a professorial thesis based on independent...
, the advanced degree that, by the rules of German academia, qualifies the bearer for a professorship. He then held teaching and research positions at the University of Kiel
University of Kiel
The University of Kiel is a university in the city of Kiel, Germany. It was founded in 1665 as the Academia Holsatorum Chiloniensis by Christian Albert, Duke of Holstein-Gottorp and has approximately 23,000 students today...
, Syracuse University
Syracuse University
Syracuse University is a private research university located in Syracuse, New York, United States. Its roots can be traced back to Genesee Wesleyan Seminary, founded by the Methodist Episcopal Church in 1832, which also later founded Genesee College...
, and Hamburg University, before once more moving to the United States: from 1964 to 1965, he was at the Graduate Research Center of the Southwest in Dallas, and from 1965 to 1971 at the University of Texas in Austin, joining Alfred Schild
Alfred Schild
Alfred Schild was a leading American physicist, well-known for his contributions to the Golden age of general relativity ....
's group first as an associate professor and, from 1967 on, as a full professor of physics. During that time, he also held visiting professorships at the universities of Würzburg
University of Würzburg
The University of Würzburg is a university in Würzburg, Germany, founded in 1402. The university is a member of the distinguished Coimbra Group.-Name:...
and Bonn
University of Bonn
The University of Bonn is a public research university located in Bonn, Germany. Founded in its present form in 1818, as the linear successor of earlier academic institutions, the University of Bonn is today one of the leading universities in Germany. The University of Bonn offers a large number...
.
Munich
In 1970, Ehlers received an offer to join the Max Planck Institute for Physics and AstrophysicsMax Planck Institute for Physics and Astrophysics
The Max Planck Institute for Physics and Astrophysics is a former institute of the Max Planck Society in Germany. Located in Garching near Munich, it was home to scientists such as Werner Heisenberg. The institute was founded in 1958 as a successor to the Max Planck Institute for Physics in...
in Munich
Munich
Munich The city's motto is "" . Before 2006, it was "Weltstadt mit Herz" . Its native name, , is derived from the Old High German Munichen, meaning "by the monks' place". The city's name derives from the monks of the Benedictine order who founded the city; hence the monk depicted on the city's coat...
, one of the institutes of Germany's major organization for basic research, the Max Planck Society
Max Planck Society
The Max Planck Society for the Advancement of Science is a formally independent non-governmental and non-profit association of German research institutes publicly funded by the federal and the 16 state governments of Germany....
, as the director of its gravitational theory department. Ehlers' name had been brought into play by Ludwig Biermann
Ludwig Biermann
Ludwig Franz Benedict Biermann was a German astronomer.He made important contributions to astrophysics and plasma physics...
, the institute's director at the time. When he joined the institute in 1971, Ehlers also became an adjunct professor at Munich's Ludwig Maximilian University. In March 1991, the institute was split into the Max Planck Institute for Physics
Max Planck Institute for Physics
Max Planck Institute for Physics is a physics institute in Munich, Germany that specializes in High Energy Physics and Astroparticle physics. It is part of the Max-Planck-Gesellschaft and is also known as the Werner Heisenberg Institute, after its first director.It was founded as the Kaiser Wilhelm...
and the Max Planck Institute for Astrophysics
Max Planck Institute for Astrophysics
The Max Planck Institute for Astrophysics is a Max Planck Institute, located in Garching, near Munich, Bavaria, Germany. It was founded as Max Planck Institute for Physics and Astrophysics in 1958 and split up into the Max Planck Institute for Astrophysics and the Max Planck Institute for Physics...
, where Ehlers' department found a new home. Over the 24 years of his tenure, his research group was home to, among others, Gary Gibbons
Gary Gibbons
Gary William Gibbons , FRS, is a British theoretical physicist. Gibbons studied in Cambridge,where in 1969 he became a research student under the supervision of Dennis Sciama. When Sciama moved to Oxford, he became a student of Stephen Hawking, obtaining his PhD from Cambridge in 1973...
, John Stewart and Bernd Schmidt, as well as visiting scientists including Abhay Ashtekar
Abhay Ashtekar
Abhay Vasant Ashtekar is an Indian theoretical physicist. He is the Eberly Professor of Physics and the Director of the Institute for Gravitational Physics and Geometry at Pennsylvania State University. As the creator of Ashtekar variables, he is one of the founders of loop quantum gravity and its...
, Demetrios Christodoulou
Demetrios Christodoulou
Demetrios Christodoulou is a Greek mathematician and physicist, who first became well known for his proof, together with Sergiu Klainerman, of the nonlinear stability of the Minkowski spacetime...
, and Brandon Carter
Brandon Carter
Brandon Carter, FRS is an Australian theoretical physicist, best known for his work on the properties of black holes and for being the first to name and employ the anthropic principle in its contemporary form. He is a researcher at the Meudon campus of the Laboratoire Univers et Théories, part of...
.
One of Ehlers' post-docs in Munich was Reinhard Breuer, who would later go on to become the editor-in-chief of Spektrum der Wissenschaft, the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
edition of the popular-science journal Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
.
Potsdam
As German science institutions reorganized after German re-unification in 1990, Ehlers lobbied for the establishment of an institute of the Max Planck SocietyMax Planck Society
The Max Planck Society for the Advancement of Science is a formally independent non-governmental and non-profit association of German research institutes publicly funded by the federal and the 16 state governments of Germany....
dedicated to research on Einstein's theories of gravity. He was successful, and on June 9, 1994, the Max Planck Society officially decided to found the Max Planck Institute for Gravitational Physics
Max Planck Institute for Gravitational Physics
The Max Planck Institute for Gravitational Physics is a Max Planck Institute whose research is aimed at investigating Einstein’s theory of relativity and beyond: Mathematics, quantum gravity, astrophysical relativity, and gravitational wave astronomy...
in Potsdam
Potsdam
Potsdam is the capital city of the German federal state of Brandenburg and part of the Berlin/Brandenburg Metropolitan Region. It is situated on the River Havel, southwest of Berlin city centre....
. Ehlers became its founding director, as well as the leader of its department for the foundations and mathematics of general relativity, when the institute started operating on April 1, 1995. He also oversaw the founding of a second institute department devoted to gravitational wave
Gravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
research and headed by Bernard F. Schutz
Bernard F. Schutz
Bernard F. Schutz is an American physicist. His research is on Einstein's theory of general relativity, more concretely on the physics of gravitational waves. He is one of the directors and head of the astrophysics group at the Max Planck Institute for Gravitational Physics in Potsdam, Germany...
. On December 31, 1998, Ehlers retired to become founding director emeritus. He continued to work at the institute until his death on May 20, 2008.
Honours and awards
In the course of his career, Ehlers received various awards and honours. He became a member of the Berlin-Brandenburgische Akademie der Wissenschaften, the Akademie der Wissenschaften und der Literatur, MainzMainz
Mainz under the Holy Roman Empire, and previously was a Roman fort city which commanded the west bank of the Rhine and formed part of the northernmost frontier of the Roman Empire...
(1972), the Leopoldina in Halle
Halle, Saxony-Anhalt
Halle is the largest city in the German state of Saxony-Anhalt. It is also called Halle an der Saale in order to distinguish it from the town of Halle in North Rhine-Westphalia...
(1975), and the Bavarian Academy of Sciences and Humanities in Munich
Munich
Munich The city's motto is "" . Before 2006, it was "Weltstadt mit Herz" . Its native name, , is derived from the Old High German Munichen, meaning "by the monks' place". The city's name derives from the monks of the Benedictine order who founded the city; hence the monk depicted on the city's coat...
(1979). From 1995 to 1998, he served as president of the International Society on General Relativity and Gravitation
International Society on General Relativity and Gravitation
The International Society on General Relativity and Gravitation is a learned society with the goal to promote research on general relativity and gravitation. To that end, it encourages communication between relativity researchers, in particular by organizing the triennial international GR...
. He also received the 2002 Max Planck Medal
Max Planck medal
The Max Planck medal is an award for extraordinary achievements in theoretical physics. It is awarded annually by the Deutsche Physikalische Gesellschaft , the world's largest organization of physicists.-List of recipients:...
of the German Physical Society
Deutsche Physikalische Gesellschaft
The Deutsche Physikalische Gesellschaft is the world's largest organization of physicists. The DPG's worldwide membership is cited as 60,000, as of 2011...
, the Volta
Alessandro Volta
Count Alessandro Giuseppe Antonio Anastasio Gerolamo Umberto Volta was a Lombard physicist known especially for the invention of the battery in 1800.-Early life and works:...
Gold Medal of Pavia University (2005), and the medal of the Faculty of Natural Sciences of Charles University, Prague
Prague
Prague is the capital and largest city of the Czech Republic. Situated in the north-west of the country on the Vltava river, the city is home to about 1.3 million people, while its metropolitan area is estimated to have a population of over 2.3 million...
(2007).
Work
Ehlers' research was in the field of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. In particular, he made important contributions to cosmology
Cosmology
Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
, the theory of gravitational lens
Gravitational lens
A gravitational lens refers to a distribution of matter between a distant source and an observer, that is capable of bending the light from the source, as it travels towards the observer...
es and gravitational waves. His principal concern was to clarify the theory's mathematical structure and its consequences, separating rigorous proofs from heuristic conjectures.
Exact solutions
For his doctoral thesis, Ehlers turned to a question that was to shape his research far beyond his graduate studies. Exact solutionExact solution
In mathematics and especially physics, an exact solution is a solution to a problem that encapsulates the whole mathematics or physics of the problem without using an approximation.-References:*...
s of Einstein's equations – in effect, universes consistent with the laws of general relativity which are simple enough to allow for an explicit description in terms of basic mathematical expressions – play a key role when it comes to building general-relativistic models. However, general relativity is a fully covariant theory – its laws are the same, independent of which coordinates are chosen to describe a given situation. One direct consequence is that two apparently different exact solution
Exact solution
In mathematics and especially physics, an exact solution is a solution to a problem that encapsulates the whole mathematics or physics of the problem without using an approximation.-References:*...
s to Einstein's equations could, in fact, correspond the same model universe, and differ only in the coordinates used in their description. Ehlers began to look for serviceable ways of characterizing exact solutions invariantly, that is, in ways that do not depend on the choice of coordinates. To this end, he examined ways of describing the intrinsic geometric properties of the known exact solutions.
During the 1960s, following up on the groundwork of research for his doctoral thesis, Ehlers published a series of seminal papers, all but one in collaboration with colleagues from the Hamburg group. The first, written with Jordan and Wolfgang Kundt, is a systematic exposition of the properties and characteristics of exact solution
Exact solution
In mathematics and especially physics, an exact solution is a solution to a problem that encapsulates the whole mathematics or physics of the problem without using an approximation.-References:*...
s to Einstein's field equations, using tools from differential geometry such as the Petrov classification
Petrov classification
In differential geometry and theoretical physics, the Petrov classification describes the possible algebraic symmetries of the Weyl tensor at each event in a Lorentzian manifold....
of Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
s (that is, those parts of the Riemann tensor describing the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of space-time which are not constrained by Einstein's equations), isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, and conformal
Conformal
Conformal may refer to:* Conformal map, in mathematics* Conformal geometry, in mathematics* Conformal map projection, in cartography* Conformal film on a surface* Conformal coating in electronics* Conformal hypergraph, in mathematics...
transformations. This work also includes the first definition of pp-waves, a class of especially simple gravitational wave
Gravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
s, as well as their classification. There were also two treatises on gravitational radiation (one with Rainer Sachs, one with Manfred Trümper). The work with Sachs studies, among other things, vacuum solutions with special algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic properties, using the 2-component spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
formalism. It also gives a systematic exposition of the geometric properties of bundles (congruences) of light beams in terms of their expansion (simply put, how the beams converge or diverge), twist and shear (how, apart from growing or shrinking, the cross section is deformed). One of the results is the Ehlers-Sachs theorem describing the properties of the shadow produced by a narrow beam of light passing an opaque object. The tools developed in that work would prove to be essential for the discovery by Roy Kerr
Roy Kerr
Roy Patrick Kerr CNZM is a New Zealand mathematician who is best known for discovering the Kerr vacuum, an exact solution to the Einstein field equation of general relativity...
of the Kerr solution, describing a rotating black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
– arguably the most important exact solution of all. The last of these seminal papers dealt with the general-relativistic treatment of the mechanics of continuous media.
Another part of Ehlers' exploration of exact solutions in his thesis led to a result that would later prove to be important. At the time Ehlers started his research on his doctoral thesis, the Golden age of general relativity
Golden age of general relativity
The golden age of general relativity is the period roughly from 1960 to 1975 during which the study of general relativity, which had previously been regarded as something of a curiosity, entered the mainstream of theoretical physics...
had not quite begun, and the basic properties and concepts of black holes were not yet understood. In the work that led to his doctoral thesis, Ehlers proved important properties of the surface around a black hole that would later be identified as its horizon
Horizon
The horizon is the apparent line that separates earth from sky, the line that divides all visible directions into two categories: those that intersect the Earth's surface, and those that do not. At many locations, the true horizon is obscured by trees, buildings, mountains, etc., and the resulting...
, in particular that the gravitational field inside cannot be static, but must change with time.
Ehlers group
In his doctoral thesis, Ehlers pointed out a duality symmetry (a duality symmetry is said to exist whenever the laws of physics remain unchanged under the exchange of seemingly different physical quantities) between different components of the metric of a stationaryStationary
Stationary can mean:* In statistics and probability: a stationary process.* In mathematics: a stationary point.* In mathematics: a stationary set.* In physics: a time-invariant quantity, such as a constant position or temperature....
vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, which maps solutions of Einstein's field equations to other solutions. This symmetry between the tt-component of the metric and a term known as the twist potential is analogous to the duality between the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E and the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
field B in source-free electrodynamics, where the replacement E
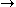–B, B 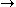E leaves Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
invariant. This duality was later generalized to an
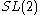symmetry which became known as the Ehlers groupEhlers group
In mathematical physics, the Ehlers group, named after Jürgen Ehlers, is a finite-dimensional transformation group of stationary vacuum spacetimes which maps solutions of Einstein's field equations to other solutions...
. Further generalizations led to the discovery of the infinite-dimensional Geroch group
Geroch group
The Geroch group is an inifinite-dimensional symmetry group of axisymmetric, stationary vacuum spacetimes that are solutions of Einstein's equations of general relativity. It is generated by two non-commuting subgroups: the Matznerg–Misner group The Geroch group is an inifinite-dimensional...
(the Geroch group is generated by two non-commuting
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s, one of which is the Ehlers group). These so-called hidden symmetries play an important role in the Kaluza-Klein reduction of both general relativity and its generalizations, such as eleven-dimensional supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
. Other applications include their use as a tool in the discovery of previously unknown solutions, and their role in a proof that solutions in the stationary axi-symmetric case form an integrable system
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
.
Cosmology: Ehlers-Geren-Sachs theorem
The Ehlers-Geren-Sachs theoremEhlers-Geren-Sachs theorem
The Ehlers-Geren-Sachs theorem, published in 1968 by Jürgen Ehlers, P. Geren and Rainer Sachs, shows that if, in a given universe, all freely falling observers measure the cosmic background radiation to have exactly the same properties in all directions , then that universe is an isotropic and...
, published in 1968 by Ehlers, P. Geren and Rainer Sachs, shows that if, in a given universe, all freely falling observers measure the cosmic background radiation to have exactly the same properties in all directions (that is, they measure the background radiation to be isotropic), then that universe is an isotropic and homogeneous FLRW spacetime.
Fundamental concepts in general relativity
Throughout his research career, Ehlers never lost sight of the fundamental concepts of Einstein's theory. In the 1960s, he collaborated with Felix Pirani and Alfred SchildAlfred Schild
Alfred Schild was a leading American physicist, well-known for his contributions to the Golden age of general relativity ....
on a constructive-axiomatic approach to general relativity: a way of deriving Einstein's theory from a minimal set of elementary objects and axioms specifying their properties. The basic ingredients of their approach are primitive concepts such as event
Event (relativity)
In physics, and in particular relativity, an event indicates a physical situation or occurrence, located at a specific point in space and time. For example, a glass breaking on the floor is an event; it occurs at a unique place and a unique time, in a given frame of reference.Strictly speaking, the...
, light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
ray, particle
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
, and freely falling particle
Free fall
Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
. At the outset, spacetime is a mere set of events, without any further structure. By postulating the basic properties of light and freely falling particles as axioms, the differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, conformal structure and, finally, the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
structure of spacetime are constructed; key steps of the construction correspond to idealized measurements, such the standard range finding used in radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
. As the final step, Einstein's equations are derived from the weakest possible set of additional axioms. The result is a formulation in which the assumptions underlying general relativity are clearly identified.
In the 1970s, in collaboration with Ekkart Rudolph, Ehlers addressed the problem of rigid bodies in general relativity. Rigid bodies are a fundamental concept in classical physics, but the fact that their different parts by definition move simultaneously is incompatible with the relativistic concept of the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
as a limiting speed for the propagation of signals and other influences. As early as 1909, Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
had given a definition of rigidity that was compatible with relativistic physics. However, this definition depends on certain assumptions that are not satisfied in a general space-time, and are also overly restrictive. Ehlers and Rudolph generalized Born's definition to a more readily applicable definition they called "pseudo-rigidity", which represents a more satisfactory approximation to the rigidity of classical physics.
Gravitational lensing
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
to be small and the deflection angles to be minute — which is perfectly sufficient for most situations of astrophysical relevance. In contrast, the monograph developed a thorough and complete description of gravitational lensing from a fully relativistic space-time perspective. This feature of the book has played a major part in the book's long-term positive reception. In the following years, Ehlers continued his research on the propagation of bundles of light in arbitrary spacetimes.
Frame theory and Newtonian gravity
A basic derivation of the Newtonian limit of general relativity is as old as the theory itself, and was used by Einstein to derive predictions such as the anomalous perihelion precession of the planet MercuryMercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
. Later work by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
, Kurt Friedrichs and others showed more concretely how a geometrical generalization of Newton's theory of gravity known as Newton-Cartan theory
Newton-Cartan theory
Newton–Cartan theory is a geometrical re-formulation, as well as a generalization, of Newtonian gravity developed by Élie Cartan. In this re-formulation, the structural similarities between Newton's theory and Albert Einstein's general theory of relativity are readily seen, and it has been used by...
could be understood as a (degenerate) limit of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, obtained by letting a specific parameter
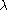go to zero. Ehlers extended this work by developing a frame theory, a mathematically precise way of constructing the Newton-Cartan limit not only of the physical laws of general relativity, but of any spacetime obeying those laws, that is, of any solution to Einstein's equations. For instance, this can be used to show that the Newtonian limit of a Schwarzschild black hole is a simple point particlePoint particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
; in addition, Newtonian versions of interesting exact solutions such as the Friedman-Lemaître models or the Gödel universe can be constructed.
Ehlers also took part in the discussion of how the back-reaction
Back-reaction
In theoretical physics, Back-reaction is often necessary to calculate the behavior of a particle or an object in an external field.When the particle is considered to be infinitely light or have an infinitesimal charge, it is said that we deal with a probe and the back-reaction is neglected...
from gravitational radiation onto a radiating system could be systematically described in a non-linear theory such as general relativity, pointing out that the standard quadrupole
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
formula for the energy flux for systems like the binary pulsar
Binary pulsar
A binary pulsar is a pulsar with a binary companion, often a white dwarf or neutron star. Binary pulsars are one of the few objects which allow physicists to test general relativity in the case of a strong gravitational field...
had not yet been rigorously derived: A priori, a derivation demanded the inclusion of higher-order terms than was commonly assumed, and in fact higher terms than were computed until then.
His work on the Newtonian limit, in particular in relation to cosmological
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
solutions, also led Ehlers, together with his former doctoral student Thomas Buchert, to a systematic study of perturbations and inhomogeneities in a Newtonian cosmos. This laid the groundwork for Buchert's later general-relativistic generalization of this treatment of inhomogeneities, the basis of his attempt to explain what is currently seen as the cosmic effects of a cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
or, in modern parlance, dark energy
Dark energy
In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...
, as a non-linear consequence of inhomogeneities in general-relativistic cosmology.
History and philosophy of physics
Complementing his interest in the foundations of general relativity and, more generally, of physics, Ehlers also did research on the history of physics. Up until his death, he collaborated in a project on the history of quantum theory at the Max Planck Institute for the History of ScienceMax Planck Institute for the History of Science
The Max Planck Institute for the History of Science in Berlin was established in March 1994. Its research is primarily devoted to a theoretically oriented history of science, principally of the natural sciences, but with methodological perspectives drawn from the cognitive sciences and from...
in Berlin. In particular, he explored Pascual Jordan's seminal contributions to the development of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
between 1925 and 1928. Throughout his career, Ehlers had an interest in the philosophical foundations and implications of physics, and contributed to research on this topic by addressing questions such as the basic status of scientific knowledge in physics.
Communicating science
Ehlers showed a keen interest in communicating his area of research to a general audience. He was a frequent public lecturer, at universities as well as at venues such as the UraniaUrania (Berlin)
Urania is a scientific society founded in Berlin in 1888. Its aim is to communicate the most recent scientific findings to the broad public. With its 2000 members, Urania organizes more than 1000 events per year which attract about 130 000 visitors...
in Berlin
Berlin
Berlin is the capital city of Germany and is one of the 16 states of Germany. With a population of 3.45 million people, Berlin is Germany's largest city. It is the second most populous city proper and the seventh most populous urban area in the European Union...
. He is the author of a number of popular-science articles, including contributions to general-audience journals such as Bild der Wissenschaft. and also edited a compilation of articles on gravity from the German edition of Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
.
Ehlers also directly addressed physics teachers, be it in talks or in journal articles on the teaching of relativity and related basic ideas of physics, such as on mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
as the language of physics.
External links
- Pages In Memoriam Jürgen Ehlers at the Albert Einstein Institute