Newton-Cartan theory
Encyclopedia
Newton–Cartan theory is a geometrical re-formulation, as well as a generalization, of Newtonian gravity developed by Élie Cartan
. In this re-formulation, the structural similarities between Newton's theory and Albert Einstein
's general theory of relativity are readily seen, and it has been used by Cartan and Kurt Friedrichs to give a rigorous formulation of the way in which Newtonian gravity can be seen as a specific limit of general relativity, and by Jürgen Ehlers
to extend this correspondence to specific solutions of general relativity.
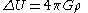
where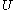
is the gravitational potential, 
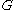is the gravitational constant and 
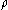is the mass density. The weak equivalence principle
motivates a geometric version of the equation of motion for a point particle in the potential
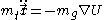
where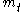
is the inertial mass and 
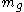the gravitational mass. Since, according to the weak equivalence principle 
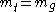, the according equation of motion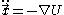
doesn't contain anymore a reference to the mass of the particle. Following the idea that the solution of the equation then is a property of the curvature of space, a connection is constructed so that the geodesic equation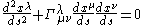
represents the equation of motion of a point particle in the potential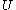
. The resulting connection is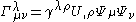
with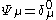
and 
(
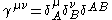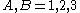). The connection has been constructed in one inertial system but can be shown to be valid in any inertial system by showing the invariance of 
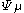and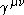 
under Galilei-transformations. The Riemann curvature tensor in inertial system coordinates of this connection is then given by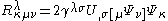
where the brackets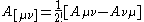
mean the antisymmetric combination of the tensor 
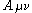. The Ricci tensor is given by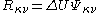
which leads to following geometric formulation of Poisson's equation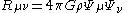
models.
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
. In this re-formulation, the structural similarities between Newton's theory and Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's general theory of relativity are readily seen, and it has been used by Cartan and Kurt Friedrichs to give a rigorous formulation of the way in which Newtonian gravity can be seen as a specific limit of general relativity, and by Jürgen Ehlers
Jürgen Ehlers
Jürgen Ehlers was a German physicist who made notable contributions to the current understanding of Albert Einstein's theory of general relativity...
to extend this correspondence to specific solutions of general relativity.
Geometric formulation of Poisson's equation
In Newton's theory of gravitation the Poisson equation reads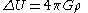where
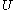is the gravitational potential, 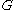is the gravitational constant and 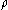is the mass density. The weak equivalence principleEquivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
motivates a geometric version of the equation of motion for a point particle in the potential
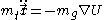
where
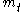is the inertial mass and 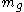the gravitational mass. Since, according to the weak equivalence principle 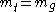, the according equation of motion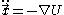doesn't contain anymore a reference to the mass of the particle. Following the idea that the solution of the equation then is a property of the curvature of space, a connection is constructed so that the geodesic equation
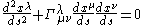
represents the equation of motion of a point particle in the potential
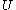. The resulting connection is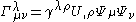with
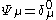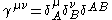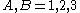and (). The connection has been constructed in one inertial system but can be shown to be valid in any inertial system by showing the invariance of 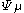and 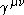under Galilei-transformations. The Riemann curvature tensor in inertial system coordinates of this connection is then given by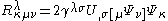where the brackets
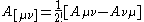mean the antisymmetric combination of the tensor 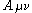. The Ricci tensor is given by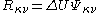which leads to following geometric formulation of Poisson's equation
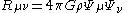
Bargmann lift
It was shown that four-dimensional Newton–Cartan theory of gravitation can be reformulated as Kaluza-Klein reduction of five-dimensional Einstein gravity along a null-like direction. This lifting is considered to be useful for non-relativistic holographicHolographic principle
The holographic principle is a property of quantum gravity and string theories which states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon...
models.