Weyl tensor
Encyclopedia
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl
, is a measure of the curvature
of spacetime
or, more generally, a pseudo-Riemannian manifold
. Like the Riemann curvature tensor
, the Weyl tensor expresses the tidal force
that a body feels when moving along a geodesic
. The Weyl tensor differs from the Riemann curvature tensor in that it does not convey information on how the volume of the body changes, but rather only how the shape of the body is distorted by the tidal force. The Ricci curvature
, or trace
component of the Riemann tensor contains precisely the information about how volumes change in the presence of tidal forces, so the Weyl tensor is the traceless component of the Riemann tensor. It is a tensor
that has the same symmetries as the Riemann tensor with the extra condition that it be trace-free: metric contraction on any pair of indices yields zero.
In general relativity
, the Weyl curvature is the only part of the curvature that exists in free space—a solution of the vacuum Einstein equation—and it governs the propagation of gravitational radiation through regions of space devoid of matter. More generally, the Weyl curvature is the only component of curvature for Ricci-flat manifold
s and always governs the characteristics
of the field equations of an Einstein manifold
.
In dimensions 2 and 3 the Weyl curvature tensor vanishes identically. In dimensions ≥ 4, the Weyl curvature is generally nonzero. If the Weyl tensor vanishes in dimension ≥ 4, then the metric is locally conformally flat
: there exists a local coordinate system in which the metric tensor is proportional to a constant tensor. This fact was a key component of Nordström's theory of gravitation
, which was an earlier precursor of general relativity
.
where n is the dimension of the manifold, g is the metric, R is the Riemann tensor, Ric is the Ricci tensor, s is the scalar curvature
, and h O k denotes the Kulkarni–Nomizu product of two symmetric (0,2) tensors:
The ordinary (1,3) valent Weyl tensor is then given by contracting the above with the inverse of the metric.
The decomposition expresses the Riemann tensor as an orthogonal direct sum, in the sense that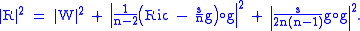
This decomposition, known as the Ricci decomposition
, expresses the Riemann curvature tensor into its irreducible components under the action of the orthogonal group
. In dimension 4, the Weyl tensor further decomposes into invariant factors for the action of the special orthogonal group, the self-dual and antiself-dual parts W+ and W−.
The Weyl tensor can also be expressed using the Schouten tensor, which is a trace-adjusted multiple of the Ricci tensor,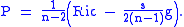
Then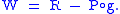
In indices,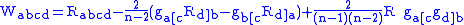
where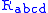
is the Riemann tensor, 
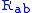is the Ricci tensor, 
is the Ricci scalar (the scalar curvature) and 
refers to the antisymmetric part. Equivalently,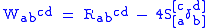
where S denotes the Schouten tensor.
changes to the metric
. That is, if g′ = f g for some positive scalar function f then the (1,3) valent Weyl tensor satisfies W′ = W. For this reason the Weyl tensor is also called the conformal tensor. It follows that a necessary condition for a Riemannian manifold to be conformally flat
is that the Weyl tensor vanish. In dimensions ≥ 4 this condition is sufficient as well. In dimension 3 the vanishing of the Cotton tensor
is a necessary and sufficient condition for the Riemannian manifold being conformally flat. Any 2-dimensional (smooth) Riemannian manifold is conformally flat, a consequence of the existence of isothermal coordinates
.
Indeed, the existence of a conformally flat scale amounts to solving the overdetermined partial differential equation
In dimension ≥ 4, the vanishing of the Weyl tensor is the only integrability condition for this equation; in dimension 3, it is the Cotton tensor
instead.
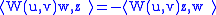
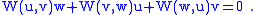
In addition, of course, the Weyl tensor is trace free: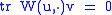
for all u, v. In indices these four conditions are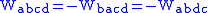
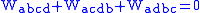
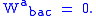
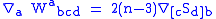
where P is the Schouten tensor. The valence (0,3) tensor on the right-hand side is the Cotton tensor
, apart from the initial factor.
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, is a measure of the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
or, more generally, a pseudo-Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. Like the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
, the Weyl tensor expresses the tidal force
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
that a body feels when moving along a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
. The Weyl tensor differs from the Riemann curvature tensor in that it does not convey information on how the volume of the body changes, but rather only how the shape of the body is distorted by the tidal force. The Ricci curvature
Ricci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
, or trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
component of the Riemann tensor contains precisely the information about how volumes change in the presence of tidal forces, so the Weyl tensor is the traceless component of the Riemann tensor. It is a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
that has the same symmetries as the Riemann tensor with the extra condition that it be trace-free: metric contraction on any pair of indices yields zero.
In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the Weyl curvature is the only part of the curvature that exists in free space—a solution of the vacuum Einstein equation—and it governs the propagation of gravitational radiation through regions of space devoid of matter. More generally, the Weyl curvature is the only component of curvature for Ricci-flat manifold
Ricci-flat manifold
In mathematics, Ricci-flat manifolds are Riemannian manifolds whose Ricci curvature vanishes. In physics, they represent vacuum solutions to the analogues of Einstein's equations for Riemannian manifolds of any dimension, with vanishing cosmological constant...
s and always governs the characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
of the field equations of an Einstein manifold
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
.
In dimensions 2 and 3 the Weyl curvature tensor vanishes identically. In dimensions ≥ 4, the Weyl curvature is generally nonzero. If the Weyl tensor vanishes in dimension ≥ 4, then the metric is locally conformally flat
Conformally flat
A Riemannian manifold is conformally flat if each point has a neighborhood that can be mapped to flat space by a conformal transformation.More formally, let be a pseudo-Riemannian manifold...
: there exists a local coordinate system in which the metric tensor is proportional to a constant tensor. This fact was a key component of Nordström's theory of gravitation
Nordström's theory of gravitation
In theoretical physics, Nordström's theory of gravitation was a predecessor of general relativity. Strictly speaking, there were actually two distinct theories proposed by the Finnish theoretical physicist Gunnar Nordström, in 1912 and 1913 respectively...
, which was an earlier precursor of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
Definition
The Weyl tensor can be obtained from the full curvature tensor by subtracting out various traces. This is most easily done by writing the Riemann tensor as a (0,4) valence tensor (by contracting with the metric). The (0,4) valence Weyl tensor is thenwhere n is the dimension of the manifold, g is the metric, R is the Riemann tensor, Ric is the Ricci tensor, s is the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
, and h O k denotes the Kulkarni–Nomizu product of two symmetric (0,2) tensors:
 |
 |
 |
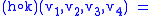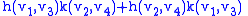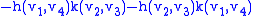The ordinary (1,3) valent Weyl tensor is then given by contracting the above with the inverse of the metric.
The decomposition expresses the Riemann tensor as an orthogonal direct sum, in the sense that
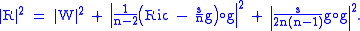
This decomposition, known as the Ricci decomposition
Ricci decomposition
In semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...
, expresses the Riemann curvature tensor into its irreducible components under the action of the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
. In dimension 4, the Weyl tensor further decomposes into invariant factors for the action of the special orthogonal group, the self-dual and antiself-dual parts W+ and W−.
The Weyl tensor can also be expressed using the Schouten tensor, which is a trace-adjusted multiple of the Ricci tensor,
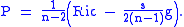
Then
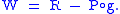
In indices,
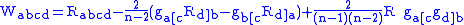
where
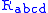is the Riemann tensor, 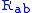is the Ricci tensor, is the Ricci scalar (the scalar curvature) and refers to the antisymmetric part. Equivalently,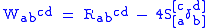where S denotes the Schouten tensor.
Conformal rescaling
The Weyl tensor has the special property that it is invariant under conformalConformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
changes to the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. That is, if g′ = f g for some positive scalar function f then the (1,3) valent Weyl tensor satisfies W′ = W. For this reason the Weyl tensor is also called the conformal tensor. It follows that a necessary condition for a Riemannian manifold to be conformally flat
Conformally flat
A Riemannian manifold is conformally flat if each point has a neighborhood that can be mapped to flat space by a conformal transformation.More formally, let be a pseudo-Riemannian manifold...
is that the Weyl tensor vanish. In dimensions ≥ 4 this condition is sufficient as well. In dimension 3 the vanishing of the Cotton tensor
Cotton tensor
In differential geometry, the Cotton tensor on a -Riemannian manifold of dimension n is a third-order tensor concomitant of the metric, like the Weyl tensor. The concept is named after Émile Cotton...
is a necessary and sufficient condition for the Riemannian manifold being conformally flat. Any 2-dimensional (smooth) Riemannian manifold is conformally flat, a consequence of the existence of isothermal coordinates
Isothermal coordinates
In mathematics, specifically in differential geometry, isothermal coordinates on a Riemannian manifoldare local coordinates where the metric isconformal to the Euclidean metric...
.
Indeed, the existence of a conformally flat scale amounts to solving the overdetermined partial differential equation
In dimension ≥ 4, the vanishing of the Weyl tensor is the only integrability condition for this equation; in dimension 3, it is the Cotton tensor
Cotton tensor
In differential geometry, the Cotton tensor on a -Riemannian manifold of dimension n is a third-order tensor concomitant of the metric, like the Weyl tensor. The concept is named after Émile Cotton...
instead.
Symmetries
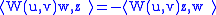
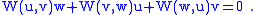
The Weyl tensor has the same symmetries as the Riemann tensor. This includes:In addition, of course, the Weyl tensor is trace free:
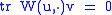
for all u, v. In indices these four conditions are
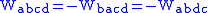
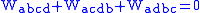
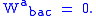
Bianchi identity
Taking traces of the usual second Bianchi identity of the Riemann tensor eventually shows that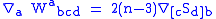where P is the Schouten tensor. The valence (0,3) tensor on the right-hand side is the Cotton tensor
Cotton tensor
In differential geometry, the Cotton tensor on a -Riemannian manifold of dimension n is a third-order tensor concomitant of the metric, like the Weyl tensor. The concept is named after Émile Cotton...
, apart from the initial factor.
See also
- Curvature of Riemannian manifoldsCurvature of Riemannian manifoldsIn mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
- Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
provides a coordinate expression for the Weyl tensor. - Petrov classificationPetrov classificationIn differential geometry and theoretical physics, the Petrov classification describes the possible algebraic symmetries of the Weyl tensor at each event in a Lorentzian manifold....
- Weyl curvature hypothesisWeyl curvature hypothesisThe Weyl curvature hypothesis, which arises in the application of Albert Einstein's general theory of relativity to physical cosmology, was introduced by the British mathematician and theoretical physicist Sir Roger Penrose in an article in 1979 in an attempt to provide explanations for two of the...
- Weyl scalar
- Cotton tensorCotton tensorIn differential geometry, the Cotton tensor on a -Riemannian manifold of dimension n is a third-order tensor concomitant of the metric, like the Weyl tensor. The concept is named after Émile Cotton...