Jordan matrix
Encyclopedia
In the mathematical
discipline of matrix theory, a Jordan block over a ring
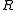(whose identities
are the zero
0 and one 1) is a matrix
composed of 0 elements everywhere except for the diagonal, which is filled with a fixed element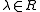
, and for the superdiagonal, which is composed of ones. The concept is named after Camille Jordan
.
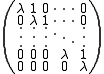
Every Jordan block is thus specified by its dimension n and its eigenvalue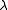
and is indicated as 
.
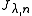Any block diagonal matrix
whose blocks are Jordan blocks is called a Jordan matrix; using either the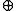
or the “
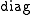” symbol, the 
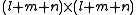block diagonal square matrix whose first diagonal block is 
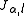, whose second diagonal block is 
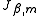and whose third diagonal block is 
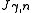is compactly indicated as 
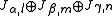or 
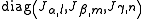, respectively.
For example the matrix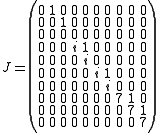
is a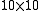
Jordan matrix with a 
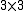block with eigenvalue 
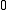, two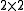 
blocks with eigenvalue the imaginary unit
and a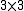
block with eigenvalue 7. Its Jordan-block structure can also be written as either 
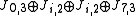or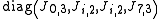 
.
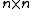square matrix 
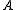whose elements are in an algebraically closed field
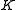is similar to a Jordan matrix 
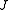, also in 
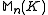, which is unique up to a permutation of its diagonal blocks themselves. 
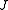is called the Jordan normal form
of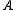
and corresponds to a generalization of the diagonalization procedure. A diagonalizable matrix
is similar, in fact, to a special case of Jordan matrix: the matrix whose blocks are all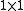
.
More generally, given a Jordan matrix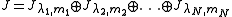
, i.e. whose 
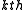diagonal block, 
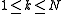is the Jordan block 
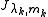and whose diagonal elements 
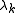may not all be distinct, it can easily be seen that the geometric multiplicity of 
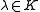for the matrix 
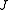, indicated as 
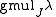, corresponds to the number of Jordan blocks whose eigenvalue is 
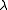. Whereas the index of an eigenvalue 
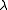for 
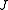, indicated as 
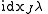, is defined as the dimension of the largest Jordan block associated to that eigenvalue.
The same goes for all the matrices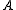
similar to 
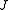, so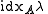 
can be defined accordingly respect to the Jordan normal form
of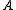
for any of its eigenvalues 
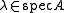. In this case one can check that the index of 
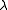for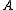 
is equal to its multiplicity as a root
of the minimal polynomial of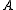
(whereas, by definition, its algebraic multiplicity for 
, 
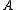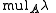, is its multiplicity as a root of the characteristic polynomial
of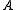
, i.e. 
).
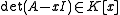An equivalent necessary and sufficient condition for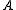
to be diagonalizable in 
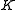is that all of its eigenvalues have index equal to 
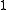, i.e. its minimal polynomial has only simple roots.
Note that knowing a matrix's spectrum with all of its algebraic/geometric multiplicities and indexes does not always allow for the computation of its Jordan normal form
(this may be a sufficient condition only for spectrally simple, usually low-dimensional matrices): the Jordan decomposition is, in general, a computationally challenging task.
From the vector space
point of view, the Jordan decomposition is equivalent to finding an orthogonal decomposition (i.e. via direct sums of eigenspaces represented by Jordan blocks) of the domain which the associated generalized eigenvector
s make a basis for.
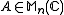(i.e. a 
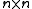complex matrix) and 
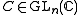be the change of basis
matrix to the Jordan normal form
of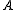
, i.e. 
.
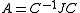Now let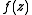
be a holomorphic function on an open set 
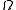such that 
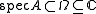, i.e. the spectrum of the matrix is contained inside the domain of holomorphy
of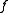
. Let
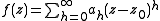
be the power series expansion of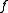
around 
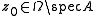, which will be hereinafter supposed to be 0 for simplicity's sake. The matrix 
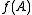is then defined via the following formal power series
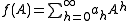
is absolutely convergent respect to the Euclidean norm of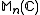
. To put it in another way, 
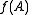converges absolutely for every square matrix whose spectral radius
is less than the radius of convergence
of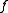
around 
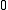and is uniformly convergent on any compact subsets of 
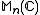satisfying this property in the matrix Lie group topology.
The Jordan normal form
allows the computation of functions of matrices without explicitly computing an infinite series, which is one of the main achievements of Jordan matrices. Using the facts that the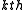
power (
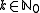) of a diagonal block matrix
is the diagonal block matrix whose blocks are the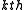
powers of the respective blocks, i.e. 
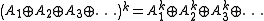, and that 
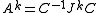, the above matrix power series becomes
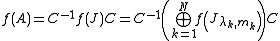
where the last series must not be computed explicitly via power series of every Jordan block. In fact, if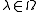
, any holomorphic function
of a Jordan block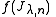
is the following upper triangular matrix
:
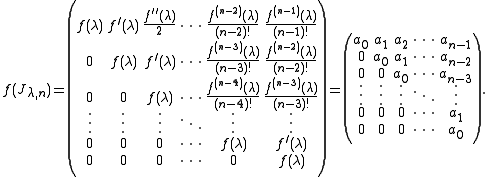
As a consequence of this, the computation of any functions of a matrix is straightforward whenever its Jordan normal form and its change-of-basis matrix are known.
Also,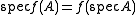
, i.e. every eigenvalue 
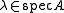corresponds to the eigenvalue 
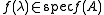, but it has, in general, different algebraic multiplicity, geometric multiplicity and index. However, the algebraic multiplicity may be computed as follows:
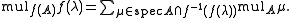
The function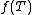
of a linear transformation
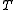between vector spaces can be defined in a similar way according to the holomorphic functional calculus
, where Banach space
and Riemann surface
theories play a fundamental role. Anyway, in the case of finite-dimensional spaces, both theories perfectly match.
is simply defined by the equation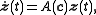
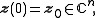
where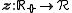
is the (
-dimensional) curve parametrization of an orbit on the Riemann surface
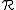of the dynamical system, whereas 
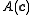is an 
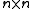complex matrix whose elements are complex functions of a 
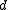-dimensional parameter 
.
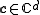Even if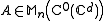
(i.e.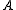 
continuously depends on the parameter 
) the Jordan normal form
of the matrix is continuously deformed almost everywhere
on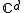
but, in general, not everywhere: there is some critical submanifold of 
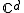which the Jordan form abruptly changes its structure whenever the parameter crosses or simply “travels” around it (monodromy
). Such changes substantially mean that several Jordan blocks (either belonging to different eigenvalues or not) join together to a unique Jordan block, or vice versa (i.e. one Jordan block splits in two or more different ones).
Many aspects of Bifurcation theory
for both continuous and discrete dynamical systems can be interpreted with the analysis of functional Jordan matrices.
From the tangent space
dynamics this means that the orthogonal decomposition of the dynamical systems' phase space
changes and, for example, different orbits gain periodicity, or lose it, or shift from a certain kind of periodicity to another (such as period-doubling, cfr. Logistic map
).
In just one sentence, the qualitative behaviour of such a dynamical system may substantially change as the versal deformation of the Jordan normal form of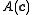
.
is a system of linear, constant-coefficients ordinary differential equations, i.e. let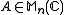
and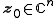 
:
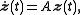
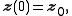
whose direct closed-form solution involves computation of the matrix exponential
:
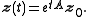
Another way, provided the solution is restricted to the local Lebesgue space of
-dimensional vector fields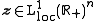 
, is to use its Laplace transform 
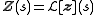. In this case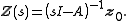
The matrix function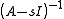
is called the resolvent matrix of the differential operator
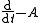. It is meromorphic with respect to the complex parameter 
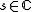since its matrix elements are rational functions whose denominator is equal for all to 
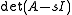. Its polar singularities are the eigenvalues of 
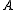, whose order equals their index for it, i.e. 
.
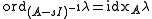Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
discipline of matrix theory, a Jordan block over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
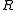(whose identitiesIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
are the zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
0 and one 1) is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
composed of 0 elements everywhere except for the diagonal, which is filled with a fixed element
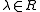, and for the superdiagonal, which is composed of ones. The concept is named after Camille JordanCamille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
.
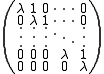
Every Jordan block is thus specified by its dimension n and its eigenvalue
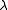and is indicated as 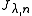.Any block diagonal matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
whose blocks are Jordan blocks is called a Jordan matrix; using either the
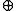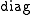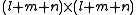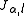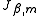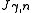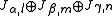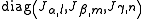or the “” symbol, the block diagonal square matrix whose first diagonal block is , whose second diagonal block is and whose third diagonal block is is compactly indicated as or , respectively.For example the matrix
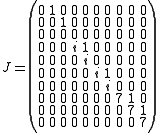
is a
Jordan matrix with a 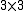block with eigenvalue 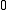, two 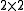blocks with eigenvalue the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
and a
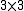block with eigenvalue 7. Its Jordan-block structure can also be written as eithe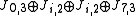r or 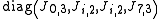.Linear algebra
Any square matrix whose elements are in an algebraically closed fieldAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
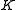is similar to a Jordan matrix 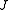, also in 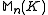, which is unique up to a permutation of its diagonal blocks themselves. 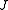is called the Jordan normal formJordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
of
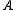and corresponds to a generalization of the diagonalization procedure. A diagonalizable matrixDiagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
is similar, in fact, to a special case of Jordan matrix: the matrix whose blocks are all
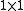.More generally, given a Jordan matrix
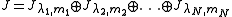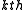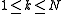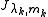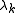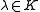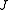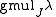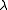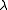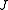, i.e. whose diagonal block, is the Jordan block and whose diagonal elements may not all be distinct, it can easily be seen that the geometric multiplicity of for the matrix , indicated as , corresponds to the number of Jordan blocks whose eigenvalue is . Whereas the index of an eigenvalue for , indicated as 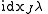, is defined as the dimension of the largest Jordan block associated to that eigenvalue.The same goes for all the matrices
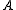similar t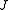o , so 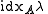can be defined accordingly respect to the Jordan normal formJordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
of
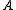for any of its eigenvalues 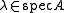. In this case one can check that the index of 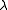for 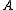is equal to its multiplicity as a rootRoot
In vascular plants, the root is the organ of a plant that typically lies below the surface of the soil. This is not always the case, however, since a root can also be aerial or aerating . Furthermore, a stem normally occurring below ground is not exceptional either...
of the minimal polynomial of
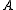(whereas, by definition, its algebraic multiplicity for 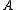, , 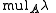is its multiplicity as a root of the characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of
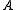, i.e. 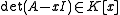).An equivalent necessary and sufficient condition for
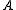to be diagonalizable in 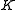is that all of its eigenvalues have index equal to 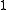, i.e. its minimal polynomial has only simple roots.Note that knowing a matrix's spectrum with all of its algebraic/geometric multiplicities and indexes does not always allow for the computation of its Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
(this may be a sufficient condition only for spectrally simple, usually low-dimensional matrices): the Jordan decomposition is, in general, a computationally challenging task.
From the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
point of view, the Jordan decomposition is equivalent to finding an orthogonal decomposition (i.e. via direct sums of eigenspaces represented by Jordan blocks) of the domain which the associated generalized eigenvector
Generalized eigenvector
In linear algebra, for a matrix A, there may not always exist a full set of linearly independent eigenvectors that form a complete basis – a matrix may not be diagonalizable. This happens when the algebraic multiplicity of at least one eigenvalue λ is greater than its geometric multiplicity...
s make a basis for.
Functions of matrices
Let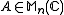 (i.e. a 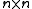complex matrix) and 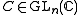be the change of basisChange of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
matrix to the Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
of
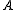, i.e. 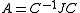.Now let
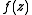be a holomorphic function on an open set 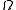such that 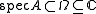, i.e. the spectrum of the matrix is contained inside the domain of holomorphyDomain of holomorphy
In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set....
of
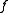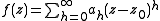
. Letbe the power series expansion of
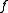around 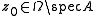, which will be hereinafter supposed to be 0 for simplicity's sake. The matrix 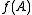is then defined via the following formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
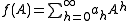
is absolutely convergent respect to the Euclidean norm of
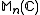. To put it in another way, 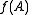converges absolutely for every square matrix whose spectral radiusSpectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
is less than the radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of
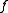around 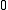and is uniformly convergent on any compact subsets of 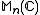satisfying this property in the matrix Lie group topology.The Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
allows the computation of functions of matrices without explicitly computing an infinite series, which is one of the main achievements of Jordan matrices. Using the facts that the
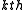power (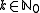) of a diagonal block matrixBlock matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
is the diagonal block matrix whose blocks are the
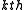powers of the respective blocks, i.e. 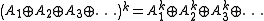, and that 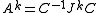, the above matrix power series becomes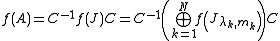where the last series must not be computed explicitly via power series of every Jordan block. In fact, if
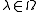, any holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
of a Jordan block
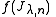is the following upper triangular matrixTriangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
:
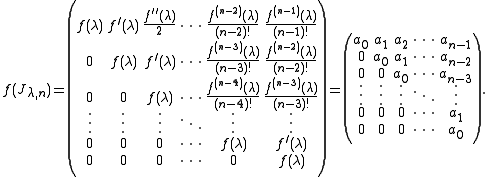
As a consequence of this, the computation of any functions of a matrix is straightforward whenever its Jordan normal form and its change-of-basis matrix are known.
Also,
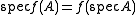, i.e. every eigenvalue 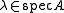corresponds to the eigenvalue 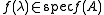, but it has, in general, different algebraic multiplicity, geometric multiplicity and index. However, the algebraic multiplicity may be computed as follows: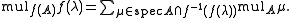The function
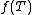of a linear transformationLinear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
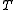between vector spaces can be defined in a similar way according to the holomorphic functional calculusHolomorphic functional calculus
In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function ƒ of a complex argument z and an operator T, the aim is to construct an operatorf\,...
, where Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
theories play a fundamental role. Anyway, in the case of finite-dimensional spaces, both theories perfectly match.
Dynamical systems
Now suppose a (complex) dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
is simply defined by the equation
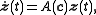
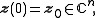
where
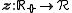is the (-dimensional) curve parametrization of an orbit on the Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
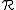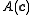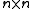of the dynamical system, whereas is an complex matrix whose elements are complex functions of a 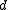-dimensional parameter 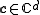.Even if
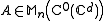(i.e. 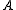continuously depends on the parameter ) the Jordan normal formJordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
of the matrix is continuously deformed almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
on
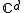but, in general, not everywhere: there is some critical submanifold of 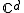which the Jordan form abruptly changes its structure whenever the parameter crosses or simply “travels” around it (monodromyMonodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
). Such changes substantially mean that several Jordan blocks (either belonging to different eigenvalues or not) join together to a unique Jordan block, or vice versa (i.e. one Jordan block splits in two or more different ones).
Many aspects of Bifurcation theory
Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
for both continuous and discrete dynamical systems can be interpreted with the analysis of functional Jordan matrices.
From the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
dynamics this means that the orthogonal decomposition of the dynamical systems' phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
changes and, for example, different orbits gain periodicity, or lose it, or shift from a certain kind of periodicity to another (such as period-doubling, cfr. Logistic map
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
).
In just one sentence, the qualitative behaviour of such a dynamical system may substantially change as the versal deformation of the Jordan normal form of
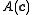.Linear ordinary differential equations
The most simple example of dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
is a system of linear, constant-coefficients ordinary differential equations, i.e. let
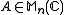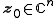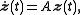
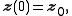
and :whose direct closed-form solution involves computation of the matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
:
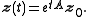
Another way, provided the solution is restricted to the local Lebesgue space of
-dimensional vector fields 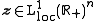, is to use its Laplace transform 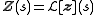. In this case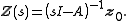The matrix function
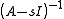is called the resolvent matrix of the differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
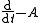. It is meromorphic with respect to the complex parameter 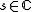since its matrix elements are rational functions whose denominator is equal for all to 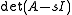. Its polar singularities are the eigenvalues of 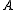, whose order equals their index for it, i.e. 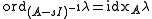.See also
- Jordan decomposition
- Jordan normal formJordan normal formIn linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
- Holomorphic functional calculusHolomorphic functional calculusIn mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function ƒ of a complex argument z and an operator T, the aim is to construct an operatorf\,...
- Matrix exponentialMatrix exponentialIn mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
- Logarithm of a matrixLogarithm of a matrixIn mathematics, a logarithm of a matrix is another matrix such that the matrix exponential of the latter matrix equals the original matrix. It is thus a generalization of the scalar logarithm and in some sense an inverse function of the matrix exponential. Not all matrices have a logarithm and...
- Dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
- Bifurcation theoryBifurcation theoryBifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
- State space (controls)State space (controls)In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...