Change of basis
Encyclopedia
In linear algebra
, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases
.
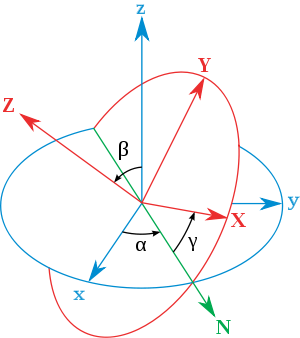There are several ways to describe a basis for the space. Some are made ad-hoc for a specific dimension. For example, there are several ways
to give a basis in dim 3, like Euler angles
.
The general case is to give the components of the new basis vectors in its current basis. This is also the more general method because it can express any possible set of vectors. This matrix can be seen as three things:
Basis Matrix: Is a matrix that represents the basis, because its columns are the vectors of the basis.
Rotation operator: When orthonormal bases are used, any other orthonormal basis can be defined by a rotation
matrix. The matrix of the rotation operator that rotates the vectors of the basis to the new one. The matrix of the rotation operator is exactly the same matrix of vectors because the rotation matrix multiplied by the identity matrix I has to be the basis matrix.
Change of basis matrix: This matrix will be used to change different objects of the space to the new basis. Therefore is called "change of basis" matrix, though some objects change with its inverse. It also represents the coefficients of any vector of the new basis as linear combinations of the current basis.
in n-dimensional space can be uniquely expressed by a linear combination
of basis vectors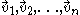
.
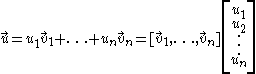
If we are given a new basis W, we need to know the new vectors as linear span of the old ones:
It is customary to express the whole new basis coefficients with a single matrix whose columns are the components of each vector in the current basis of the space:
With this matrix we can write in a relaxed way:
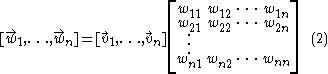
The new components of the same vector u will be called [u']. Substituting (2) inside its expression we have:
Therefore comparing the two previous expressions and inverting the matrix:
This shows that vectors change with the inverse of the basis matrix.
we can write:
where W is the matrix of the basis, with the components of its vectors in columns [W] =
.
A vector u will have components [u] and [u'] in both bases. Substituting (1) in the second and comparing both:
it follows that that:
And representing the elements of the inverse of W with a tilde over them:
As we wanted to prove.
Substituting this in the first expression:
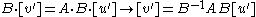
Therefore the matrix in the new basis is
being B the matrix of the given basis.
Therefore linear maps are said to be 1-co 1-contra variants objects.
Using tensor notation, with a hat for the new matrix and tildes for the B-inverted elements, the new matrix of components is:
.
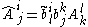
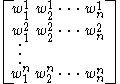As it was shown before, representing the elements of the inverse of W with a tilde over them, and the new components with a hat:
and for a linear map:
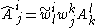
The components of a general tensor
transform in a similar manner with a transformation matrix for each index. If an index transforms like a vector with the inverse of the basis transformation, it is called contravariant and is traditionally denoted with an upper index, while an index that transforms with the basis transformation itself is called covariant and is denoted with a lower index. The transformation law for a rank m tensor with n contravariant indices and m−n covariant indices is thus given as,
Such a tensor is said to be of order or type .There is a plethora of different terminology for this around. The terms order, type, rank, valence, and degree are in use for the same concept. This article uses the term "order" or "total order" for the total dimension of the array (or its generalisation in other definitions) m in the preceding example, and the term type for the pair giving the number contravariant and covariant indices. A tensor of type will also be referred to as a "" tensor for short.
s are covariant objects. Their components change directly with the basis matrix.
Other objects of the space have different variance. For instance, a linear map is a 1-covariant, 1-contravariant object.
Now, if a vector u is covariant, its components do not change with basis, [u]w = [u]v. However, they do when looking from the fixed basis. For instance, as the components switch W → (WP = V), the components in basis W leap [u]w → P[u]w:
More often, a passive transformation is meant. The vectors in the space are considered contravariant, which are preserved, u = V[u]v = W[u]w, by compensating the basis transformation through the opposite transformation. That is, as basis scales up by P in W → (V = WP), the components must be scaled down by the same factor, [u]w → (P−1[u]w = [u]v). The net identity transform, I = PP−1, is applied to the vector:
Applying the basis transformation matrix on the left, W → PW, is not widespread, though it can be reduced to the considered W → WP case by PW = (WW−1)PW = W(W−1PW) = WP'.
The change of basis can be applied not only to the component representations of vectors but, at higher level, to the matrices which are component representations of linear transformations.
Since the bases are related by some coordinate transforms, [y]Y2 = PY2Y1 [y]Y1 and [x]X2 = PX2X1 [x]X1, the first form can be rewritten
Multiplying both sides by PY2Y1
allows to compare with the second form:
This relationship is known as equivalence transformation and matrix [L]Y2X2 is equivalent to [L]Y1X1 when it holds. A special case of equivalence, called matrix similarity takes place when dimensions of range and domain match and bases are transformed by the same factor, PY2Y1 = PX2X1 = P, resulting
The equivalent matrices, therefore, expose the same linear mapping in different bases by making intermediate transition into the old basis, where matrix is known. In the eigenvector basis, the matrix takes the simplest, diagonal
, representation.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
.
Expression of a basis
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
to give a basis in dim 3, like Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
.
The general case is to give the components of the new basis vectors in its current basis. This is also the more general method because it can express any possible set of vectors. This matrix can be seen as three things:
Basis Matrix: Is a matrix that represents the basis, because its columns are the vectors of the basis.
Rotation operator: When orthonormal bases are used, any other orthonormal basis can be defined by a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
matrix. The matrix of the rotation operator that rotates the vectors of the basis to the new one. The matrix of the rotation operator is exactly the same matrix of vectors because the rotation matrix multiplied by the identity matrix I has to be the basis matrix.
Change of basis matrix: This matrix will be used to change different objects of the space to the new basis. Therefore is called "change of basis" matrix, though some objects change with its inverse. It also represents the coefficients of any vector of the new basis as linear combinations of the current basis.
Change of basis for vectors
Any vector in n-dimensional space can be uniquely expressed by a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of basis vectors
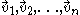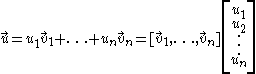
.If we are given a new basis W, we need to know the new vectors as linear span of the old ones:
It is customary to express the whole new basis coefficients with a single matrix whose columns are the components of each vector in the current basis of the space:
- [W] =
.
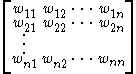With this matrix we can write in a relaxed way:
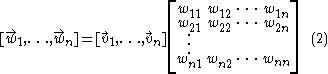
The new components of the same vector u will be called [u']. Substituting (2) inside its expression we have:
Therefore comparing the two previous expressions and inverting the matrix:
This shows that vectors change with the inverse of the basis matrix.
Tensor proof
We will prove that the components of a vector change with the inverse of the basis. Let be the N vectors of the basis W a linear span of those of V. Using Einstein notationEinstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
we can write:
where W is the matrix of the basis, with the components of its vectors in columns [W] =
.A vector u will have components [u] and [u'] in both bases. Substituting (1) in the second and comparing both:
it follows that that:
And representing the elements of the inverse of W with a tilde over them:
As we wanted to prove.
Change of basis of a linear map
Given a linear map whose matrix is A, in the basis B of the space in transforms vectors coordinates [u] as [v]=A⋅[u]. As vectors change with the inverse of B, its inverse transformation is [v]=B⋅[v'].Substituting this in the first expression:
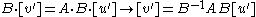
Therefore the matrix in the new basis is
being B the matrix of the given basis.
Therefore linear maps are said to be 1-co 1-contra variants objects.
Using tensor notation, with a hat for the new matrix and tildes for the B-inverted elements, the new matrix of components is:
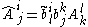
Change of basis for a general tensor
Let W be the matrix of a new basis, with the components of its vectors in columns [W] =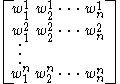.As it was shown before, representing the elements of the inverse of W with a tilde over them, and the new components with a hat:
and for a linear map:
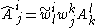
The components of a general tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
transform in a similar manner with a transformation matrix for each index. If an index transforms like a vector with the inverse of the basis transformation, it is called contravariant and is traditionally denoted with an upper index, while an index that transforms with the basis transformation itself is called covariant and is denoted with a lower index. The transformation law for a rank m tensor with n contravariant indices and m−n covariant indices is thus given as,
Such a tensor is said to be of order or type .There is a plethora of different terminology for this around. The terms order, type, rank, valence, and degree are in use for the same concept. This article uses the term "order" or "total order" for the total dimension of the array (or its generalisation in other definitions) m in the preceding example, and the term type for the pair giving the number contravariant and covariant indices. A tensor of type will also be referred to as a "" tensor for short.
Contravariance and covariance considerations
We have shown that the elements of a linear space are contravariant objects. They change with the inverse of the basis matrix. Not every object of a space behaves this way. For example, linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s are covariant objects. Their components change directly with the basis matrix.
Other objects of the space have different variance. For instance, a linear map is a 1-covariant, 1-contravariant object.
Now, if a vector u is covariant, its components do not change with basis, [u]w = [u]v. However, they do when looking from the fixed basis. For instance, as the components switch W → (WP = V), the components in basis W leap [u]w → P[u]w:
- V([u]v) = WP([u]w) = W(P[u]w) ≠ W[u]w.
More often, a passive transformation is meant. The vectors in the space are considered contravariant, which are preserved, u = V[u]v = W[u]w, by compensating the basis transformation through the opposite transformation. That is, as basis scales up by P in W → (V = WP), the components must be scaled down by the same factor, [u]w → (P−1[u]w = [u]v). The net identity transform, I = PP−1, is applied to the vector:
- W[u]w = W(PP-1)[u]w = (WP)(P-1[u]w) = V[u]v.
Applying the basis transformation matrix on the left, W → PW, is not widespread, though it can be reduced to the considered W → WP case by PW = (WW−1)PW = W(W−1PW) = WP'.
The change of basis can be applied not only to the component representations of vectors but, at higher level, to the matrices which are component representations of linear transformations.
Linear transformations
The translation of vector coordinates due to basis change is formally equivalent to active linear transformation; both are represented by the same square matrices. If a linear transformation, L, takes vector x from one space with bases X1 and X2 to a vector y = Lx in another space with bases Y1 and Y2, it then can be expressed in the matrix forms- [y]Y1 = [L]Y1X1 [x]X1 or
- [y]Y2 = [L]Y2X2 [x]X2
Since the bases are related by some coordinate transforms, [y]Y2 = PY2Y1 [y]Y1 and [x]X2 = PX2X1 [x]X1, the first form can be rewritten
- P-1Y2Y1 [y]Y2 = [L]Y1X1 P-1X2X1 [x]X2.
Multiplying both sides by PY2Y1
- [y]Y2 = PY2Y1 [L]Y1X1 P-1X2X1 [x]X2
allows to compare with the second form:
- [L]Y2X2 = PY2Y1 [L]Y1X1 P-1X2X1.
This relationship is known as equivalence transformation and matrix [L]Y2X2 is equivalent to [L]Y1X1 when it holds. A special case of equivalence, called matrix similarity takes place when dimensions of range and domain match and bases are transformed by the same factor, PY2Y1 = PX2X1 = P, resulting
- [L]2 = P [L]1 P-1.
The equivalent matrices, therefore, expose the same linear mapping in different bases by making intermediate transition into the old basis, where matrix is known. In the eigenvector basis, the matrix takes the simplest, diagonal
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
, representation.
See also
- Integral transform, the continuous analogue of change of basis.
- Active and passive transformationActive and passive transformationIn the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system . The distinction between...
External links
- MIT Linear Algebra Lecture on Change of Bases at MIT OpenCourseWare