
Sackur-Tetrode equation
Encyclopedia
The Sackur–Tetrode equation is an expression for the entropy
of a monatomic classical ideal gas
which incorporates quantum considerations which give a more detailed description of its regime of validity.
The Sackur–Tetrode equation is named for Hugo Martin Tetrode (1895–1931) and Otto Sackur
(1880–1914), who developed it independently as a solution of Boltzmann's gas statistics and entropy equations, at about the same time in 1912.
The Sackur–Tetrode equation is written:
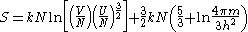
where V is the volume of the gas, N is the number of particles in the gas, U is the internal energy of the gas, k is Boltzmann's constant, m is the mass of a gas particle, h is Planck's constant and ln is the natural logarithm
. See Gibbs paradox
for a derivation of the Sackur–Tetrode equation. See also the ideal gas
article for the constraints placed upon the entropy of an ideal gas by thermodynamics alone.
The Sackur–Tetrode equation can also be conveniently expressed in terms of the thermal wavelength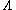 . Using the classical ideal gas
. Using the classical ideal gas
relationship U = C*NkT (where C* is the dimensionless specific heat capacity
) yields:
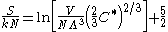
Note that the assumption was made that the gas is in the classical regime, and is described by Maxwell–Boltzmann statistics
(with "correct Boltzmann counting"). From the definition of the thermal wavelength, this means the Sackur–Tetrode equation is only valid for
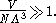
and in fact, the entropy predicted by the Sackur–Tetrode equation approaches negative infinity as the temperature approaches zero.
, at standard pressure
(100 kPa or 101.325 kPa, to be specified), for one mole
of an ideal gas composed of particles of mass equal to one atomic mass unit
(mu = ). Its 2006 CODATA recommended value is:
the tools of information theory
can be used to provide an information perspective of entropy. The physical chemist Arieh Ben-Naim
rederived the Sackur–Tetrode equation for entropy in terms of information theory, and in doing so he tied in well known concepts from modern physics
. He showed the equation to consist of stacking the entropy (missing information) due to four terms: positional uncertainty, momenta uncertainty, quantum mechanical uncertainty principle
and the indistinguishability of the particles.
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of a monatomic classical ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
which incorporates quantum considerations which give a more detailed description of its regime of validity.
The Sackur–Tetrode equation is named for Hugo Martin Tetrode (1895–1931) and Otto Sackur
Otto Sackur
Otto Sackur was a German physical chemist.He is known for the development of the Sackur-Tetrode equation which he developed independently of Hugo Tetrode...
(1880–1914), who developed it independently as a solution of Boltzmann's gas statistics and entropy equations, at about the same time in 1912.
The Sackur–Tetrode equation is written:
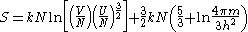
where V is the volume of the gas, N is the number of particles in the gas, U is the internal energy of the gas, k is Boltzmann's constant, m is the mass of a gas particle, h is Planck's constant and ln is the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
. See Gibbs paradox
Gibbs paradox
In statistical mechanics, a semi-classical derivation of the entropy that doesn't take into account the indistinguishability of particles, yields an expression for the entropy which is not extensive...
for a derivation of the Sackur–Tetrode equation. See also the ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
article for the constraints placed upon the entropy of an ideal gas by thermodynamics alone.
The Sackur–Tetrode equation can also be conveniently expressed in terms of the thermal wavelength
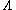 . Using the classical ideal gas
. Using the classical ideal gasIdeal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
relationship U = C*NkT (where C* is the dimensionless specific heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
) yields:
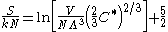
Note that the assumption was made that the gas is in the classical regime, and is described by Maxwell–Boltzmann statistics
Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
(with "correct Boltzmann counting"). From the definition of the thermal wavelength, this means the Sackur–Tetrode equation is only valid for
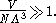
and in fact, the entropy predicted by the Sackur–Tetrode equation approaches negative infinity as the temperature approaches zero.
Sackur–Tetrode constant
The Sackur–Tetrode constant, written S0/R, is equal to S/kN evaluated at a temperature of T = 1 kelvinKelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
, at standard pressure
Standard state
In chemistry, the standard state of a material is a reference point used to calculate its properties under different conditions. In principle, the choice of standard state is arbitrary, although the International Union of Pure and Applied Chemistry recommends a conventional set of standard states...
(100 kPa or 101.325 kPa, to be specified), for one mole
Mole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
of an ideal gas composed of particles of mass equal to one atomic mass unit
Atomic mass unit
The unified atomic mass unit or dalton is a unit that is used for indicating mass on an atomic or molecular scale. It is defined as one twelfth of the rest mass of an unbound neutral atom of carbon-12 in its nuclear and electronic ground state, and has a value of...
(mu = ). Its 2006 CODATA recommended value is:
- S0/R = −1.151 7047(44) for p
o= 100 kPa - S0/R = −1.164 8677(44) for p
o= 101.325 kPa
Interpretation of the equation through information theory
In addition to using the thermodynamic perspective of entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
the tools of information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
can be used to provide an information perspective of entropy. The physical chemist Arieh Ben-Naim
Arieh Ben-Naim
Arieh Ben-Naim is a professor of physical chemistry in the Hebrew University of Jerusalem. He has made major contributions over 40 years to the theory of the structure of water, aqueous solutions and hydrophobic-hydrophilic interactions...
rederived the Sackur–Tetrode equation for entropy in terms of information theory, and in doing so he tied in well known concepts from modern physics
Modern physics
The term modern physics refers to the post-Newtonian conception of physics. The term implies that classical descriptions of phenomena are lacking, and that an accurate, "modern", description of reality requires theories to incorporate elements of quantum mechanics or Einsteinian relativity, or both...
. He showed the equation to consist of stacking the entropy (missing information) due to four terms: positional uncertainty, momenta uncertainty, quantum mechanical uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
and the indistinguishability of the particles.

