Gas in a box
Encyclopedia
In quantum mechanics
, the results of the quantum particle in a box
can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions. This simple model can be used to describe the classical ideal gas
as well as the various quantum ideal gases such as the ideal massive Fermi gas
, the ideal massive Bose gas
as well as black body
radiation which may be treated as a massless Bose gas, in which thermalization is usually assumed to be facilitated by the interaction of the photons with an equilibrated mass.
Using the results from either Maxwell-Boltzmann statistics, Bose-Einstein statistics or Fermi-Dirac statistics
, and considering the limit of a very large box, the Thomas-Fermi approximation is used to express the degeneracy of the energy states as a differential, and summations over states as integrals. This enables thermodynamic properties of the gas to be calculated with the use of the partition function
or the grand partition function. These results will be applied to both massive and massless particles. More complete calculations will be left to separate articles, but some simple examples will be given in this article.
enumerated by a set of quantum numbers
[nx, ny, nz]. The magnitude of the momentum is given by
where h is Planck's constant and L is the length of a side of the box.
Each possible state of a particle can be thought of as a point on a 3-dimensional
grid of positive integers. The distance from the origin to any point will be
Suppose each set of quantum numbers specify f states where f is
the number of internal degrees of freedom of the particle that can be altered by
collision. For example, a spin 1/2 particle would have f=2, one for each spin
state. For large values of n , the number of states with magnitude of momentum less than or equal to p from the above
equation is approximately
which is just f times the volume of a sphere of radius n divided by eight
since only the octant with positive ni is considered. Using a continuum approximation, the number of
states with magnitude of momentum between p and p+dp is
therefore
where V=L3 is the volume of the box. Notice that in using this
continuum approximation, the ability to characterize the low-energy
states is lost, including the ground state where ni =1. For most cases this
will not be a problem, but when considering Bose-Einstein condensation, in which a
large portion of the gas is in or near the ground state, the
ability to deal with low energy states becomes important.
Without using the continuum approximation, the number of particles with
energy εi is given by
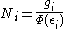
where
Using the continuum approximation, the number of particles dNE with energy between
E and E+dE is:
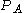for a variable 
is defined through the expression 
which is the fraction of particles that have values for 
between 
and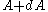 
where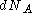
, number of particles which have values for 
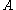between 
and 
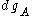, number of states which have values for 
between 
and 
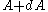
, probability that a state which has the value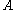 
is occupied by a particle
It follows that:
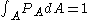
For a momentum distribution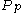
, the fraction of particles with magnitude of momentum between 
and 
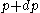is:
and for an energy distribution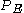
, the fraction of particles with energy between 
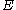and 
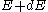is:
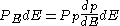
For a particle in a box (and for a free particle as well), the relationship between energy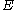
and momentum 
is different for massive and massless particles. For massive particles,
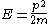
while for massless particles,
where
is the mass of the particle and 
is the speed of light.
Using these relationships,
where Λ is the thermal wavelength of the gas.
This is an important quantity, since when Λ is on the order of the
inter-particle distance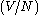
1/3, quantum effects begin to
dominate and the gas can no longer be considered to be a Maxwell-Boltzmann gas.
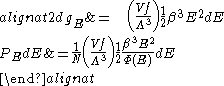
where Λ is now the thermal wavelength for massless particles.
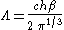
Integrating the energy distribution function and solving for N gives
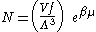
Substituting into the original energy distribution function gives
which are the same results obtained classically for the
Maxwell-Boltzmann distribution. Further results can be found in the classical section of the article on the ideal gas
.
Integrating the energy distribution function and solving for N gives
the particle number
where Lis(z) is the polylogarithm function and Λ is the
thermal wavelength. The polylogarithm term must always be positive
and real, which means its value will go from 0 to ζ(3/2) as z goes from
0 to 1. As the temperature drops towards zero, Λ will become larger and larger,
until finally Λ will reach a critical value Λc where z=1 and
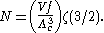
The temperature at which Λ=Λc is the critical temperature. For
temperatures below this critical temperature, the above equation for the particle number
has no solution. The critical temperature is the temperature at which a Bose-Einstein
condensate begins to form. The problem is, as mentioned
above, that the ground state has been ignored in the continuum approximation. It turns
out, however, that the above equation for particle number expresses the number of bosons in excited states
rather well, and thus:
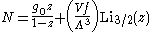
where the added term is the number of particles in the ground state. (The ground
state energy has been ignored.) This equation will hold down to zero temperature.
Further results can be found in the article on the ideal Bose gas
.
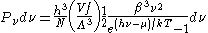
where Λ is the thermal wavelength for massless particles. The spectral energy density (energy per unit volume per unit frequency) is then
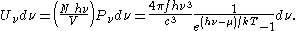
Other thermodynamic parameters may be derived analogously to the case for massive particles. For example, integrating the frequency distribution function and solving for N gives the number of particles:
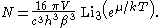
The most common massless Bose gas is a photon gas
in a black body
. Taking the "box" to be a black body cavity, the photons are continually being absorbed and re-emitted by the walls. When this is the case, the number of photons is not conserved. In the derivation of Bose-Einstein statistics, when the restraint on the number of particles is removed, this is effectively the same as setting the chemical potential (μ) to zero. Furthermore, since photons have two spin states, the value of f is 2. The spectral energy density is then
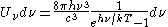
which is just the spectral energy density for Planck's law of black body radiation
. Note that the Wien distribution is recovered if this procedure is carried out for massless Maxwell-Boltzmann particles, which approximates a Planck's distribution for high temperatures or low densities.
In certain situations, the reactions involving photons will result in the conservation of the number of photons (e.g. light-emitting diode
s, "white" cavities). In these cases, the photon distribution function will involve a non-zero chemical potential. (Hermann 2005)
Another massless Bose gas is given by the Debye model
for heat capacity. This considers a gas of phonons in a box and differs from the development for photons in that the speed of the phonons is less than light speed, and there is a maximum allowed wavelength for each axis of the box. This means that the integration over phase space cannot be carried out to infinity, and instead of results being expressed in polylogarithms, they are expressed in the related Debye functions.
Integrating the energy distribution function gives
where again, Lis(z) is the polylogarithm function and Λ is the
thermal de Broglie wavelength. Further results can be found in the article on the
ideal Fermi gas
.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the results of the quantum particle in a box
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions. This simple model can be used to describe the classical ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
as well as the various quantum ideal gases such as the ideal massive Fermi gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
, the ideal massive Bose gas
Bose gas
An ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
as well as black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
radiation which may be treated as a massless Bose gas, in which thermalization is usually assumed to be facilitated by the interaction of the photons with an equilibrated mass.
Using the results from either Maxwell-Boltzmann statistics, Bose-Einstein statistics or Fermi-Dirac statistics
Fermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
, and considering the limit of a very large box, the Thomas-Fermi approximation is used to express the degeneracy of the energy states as a differential, and summations over states as integrals. This enables thermodynamic properties of the gas to be calculated with the use of the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
or the grand partition function. These results will be applied to both massive and massless particles. More complete calculations will be left to separate articles, but some simple examples will be given in this article.
Thomas-Fermi approximation for the degeneracy of states
For both massive and massless particles in a box, the states of a particle areenumerated by a set of quantum numbers
[nx, ny, nz]. The magnitude of the momentum is given by
where h is Planck's constant and L is the length of a side of the box.
Each possible state of a particle can be thought of as a point on a 3-dimensional
grid of positive integers. The distance from the origin to any point will be
Suppose each set of quantum numbers specify f states where f is
the number of internal degrees of freedom of the particle that can be altered by
collision. For example, a spin 1/2 particle would have f=2, one for each spin
state. For large values of n , the number of states with magnitude of momentum less than or equal to p from the above
equation is approximately
which is just f times the volume of a sphere of radius n divided by eight
since only the octant with positive ni is considered. Using a continuum approximation, the number of
states with magnitude of momentum between p and p+dp is
therefore
where V=L3 is the volume of the box. Notice that in using this
continuum approximation, the ability to characterize the low-energy
states is lost, including the ground state where ni =1. For most cases this
will not be a problem, but when considering Bose-Einstein condensation, in which a
large portion of the gas is in or near the ground state, the
ability to deal with low energy states becomes important.
Without using the continuum approximation, the number of particles with
energy εi is given by
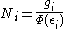
where
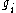 , degeneracyDegenerate energy level In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more... of state i |
 |
| with β = 1/kT , Boltzmann's constant k, temperature Temperature Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot... T, and chemical potential Chemical potential Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system... μ . |
| (See Maxwell-Boltzmann statistics, Bose-Einstein statistics, and Fermi-Dirac statistics Fermi-Dirac statistics Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle... .) |
Using the continuum approximation, the number of particles dNE with energy between
E and E+dE is:
- where
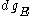is the number of states with energy between E and E+dE .
Energy distribution
Using the results derived from the previous sections of this article, some distributions for the "gas in a box" can now be determined. For a system of particles, the distribution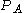 for a variable is defined through the expression which is the fraction of particles that have values for between and 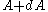where
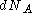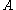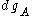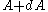
, number of particles which have values for between and , number of states which have values for between and , probability that a state which has the value 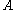is occupied by a particle
-
, total number of particles.
It follows that:
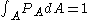
For a momentum distribution
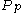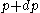, the fraction of particles with magnitude of momentum between and is:and for an energy distribution
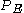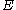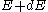, the fraction of particles with energy between and is: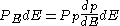For a particle in a box (and for a free particle as well), the relationship between energy
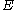and momentum is different for massive and massless particles. For massive particles,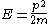while for massless particles,
where
is the mass of the particle and is the speed of light.Using these relationships,
- For massive particles
where Λ is the thermal wavelength of the gas.
This is an important quantity, since when Λ is on the order of the
inter-particle distance
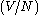1/3, quantum effects begin todominate and the gas can no longer be considered to be a Maxwell-Boltzmann gas.
- For massless particles
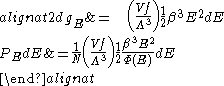
where Λ is now the thermal wavelength for massless particles.
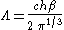
Massive Maxwell-Boltzmann particles
For this case:Integrating the energy distribution function and solving for N gives
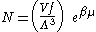
Substituting into the original energy distribution function gives
which are the same results obtained classically for the
Maxwell-Boltzmann distribution. Further results can be found in the classical section of the article on the ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
.
Massive Bose-Einstein particles
For this case:- where
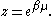
Integrating the energy distribution function and solving for N gives
the particle number
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
where Lis(z) is the polylogarithm function and Λ is the
thermal wavelength. The polylogarithm term must always be positive
and real, which means its value will go from 0 to ζ(3/2) as z goes from
0 to 1. As the temperature drops towards zero, Λ will become larger and larger,
until finally Λ will reach a critical value Λc where z=1 and
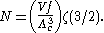
The temperature at which Λ=Λc is the critical temperature. For
temperatures below this critical temperature, the above equation for the particle number
has no solution. The critical temperature is the temperature at which a Bose-Einstein
condensate begins to form. The problem is, as mentioned
above, that the ground state has been ignored in the continuum approximation. It turns
out, however, that the above equation for particle number expresses the number of bosons in excited states
rather well, and thus:
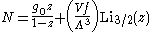
where the added term is the number of particles in the ground state. (The ground
state energy has been ignored.) This equation will hold down to zero temperature.
Further results can be found in the article on the ideal Bose gas
Bose gas
An ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
.
Massless Bose-Einstein particles (e.g. black body radiation)
For the case of massless particles, the massless energy distribution function must be used. It is convenient to convert this function to a frequency distribution function: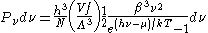where Λ is the thermal wavelength for massless particles. The spectral energy density (energy per unit volume per unit frequency) is then
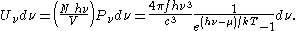
Other thermodynamic parameters may be derived analogously to the case for massive particles. For example, integrating the frequency distribution function and solving for N gives the number of particles:
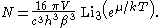
The most common massless Bose gas is a photon gas
Photon gas
In physics, a photon gas is a gas-like collection of photons, which has many of the same properties of a conventional gas like hydrogen or neon - including pressure, temperature, and entropy...
in a black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
. Taking the "box" to be a black body cavity, the photons are continually being absorbed and re-emitted by the walls. When this is the case, the number of photons is not conserved. In the derivation of Bose-Einstein statistics, when the restraint on the number of particles is removed, this is effectively the same as setting the chemical potential (μ) to zero. Furthermore, since photons have two spin states, the value of f is 2. The spectral energy density is then
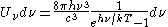
which is just the spectral energy density for Planck's law of black body radiation
Planck's law of black body radiation
In physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
. Note that the Wien distribution is recovered if this procedure is carried out for massless Maxwell-Boltzmann particles, which approximates a Planck's distribution for high temperatures or low densities.
In certain situations, the reactions involving photons will result in the conservation of the number of photons (e.g. light-emitting diode
Light-emitting diode
A light-emitting diode is a semiconductor light source. LEDs are used as indicator lamps in many devices and are increasingly used for other lighting...
s, "white" cavities). In these cases, the photon distribution function will involve a non-zero chemical potential. (Hermann 2005)
Another massless Bose gas is given by the Debye model
Debye model
In thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice as phonons in a box, in contrast to the Einstein model, which treats the...
for heat capacity. This considers a gas of phonons in a box and differs from the development for photons in that the speed of the phonons is less than light speed, and there is a maximum allowed wavelength for each axis of the box. This means that the integration over phase space cannot be carried out to infinity, and instead of results being expressed in polylogarithms, they are expressed in the related Debye functions.
Massive Fermi-Dirac particles (e.g. electrons in a metal)
For this case:Integrating the energy distribution function gives
where again, Lis(z) is the polylogarithm function and Λ is the
thermal de Broglie wavelength. Further results can be found in the article on the
ideal Fermi gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
.