Saha ionization equation
Encyclopedia
The Saha ionization equation, also known as the Saha–Langmuir equation, was developed by the Indian astrophysicist Meghnad Saha
in 1920, and later (1923) by Irving Langmuir
. One of the important applications of the equation was in explaining the spectral classification of stars. The equation is a result of combining ideas of quantum mechanics and statistical mechanics.
For a gas at a high enough temperature, the thermal collisions of the atoms will ionize some of the atoms. One or more of the electrons that are normally bound to the atom in orbits around the atomic nucleus will be ejected from the atom and will form an electron gas that co-exists with the gas of atomic ions and neutral atoms. This state of matter is called a plasma
. The Saha equation describes the degree of ionization of this plasma as a function of the temperature, density, and ionization energies of the atoms. The Saha equation only holds for weakly ionized plasmas for which the Debye length
is large. This means that the "screening" of the coulomb charge of ions and electrons by other ions and electrons is negligible. The subsequent lowering of the ionization potentials and the "cutoff" of the partition function
is therefore also negligible.
For a gas composed of a single atomic species, the Saha equation is written:
where:
In the case where only one level of ionization is important, we have
and defining the total density n as 
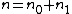, the Saha equation simplifies to:
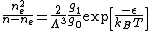
where
is the energy of ionization.
The Saha equation is useful for determining the ratio of particle densities for two different ionization levels. The most useful form of the Saha equation for this purpose is
,
where Z denotes the partition function
. The Saha equation can be seen as a restatement of the equilibrium condition for the chemical potential
s:
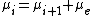
This equation simply states that the potential for an atom of ionization state i to ionize is the same as the potential for an electron and an atom of ionization state i+1; the potentials are equal, therefore the system is in equilibrium and no net change of ionization will occur.
In the early twenties Ralph H. Fowler
(in collaboration with Charles Galton Darwin
) developed a very powerful method in statistical mechanics
permitting a systematic exposition and working out of the equilibrium properties of matter. He used this to provide a (rigorous) derivation of the ionization formula which as described earlier Saha had obtained by extending (and justifiably) to ionization of atoms the theorem of Van 't Hoff
, well known in physical chemistry for its application to molecular dissociation. Also, a significant improvement in the Saha equation introduced by Fowler was to include the effect of the excited states of atoms and ions. Further, it marked an important step forward when in 1923 Edward Arthur Milne and R.H. Fowler in a paper in the Monthly Notices of the Royal Astronomical Society showed that the criterion of the maximum intensity of absorption lines (belonging to subordinate series of a neutral atom) was much more fruitful in giving information about physical parameters of stellar atmospheres than the criterion employed by Saha which consisted in the marginal appearance or disappearance of absorption lines. (The latter criterion requires some knowledge of the relevant pressures in the stellar atmospheres, and Saha following the generally accepted view at the time assumed a value of the order of 1 to 0.1 atmosphere.) To quote from E. A. Milne:
Meghnad Saha
Meghnad Saha FRS was an Indian astrophysicist best known for his development of the Saha equation, used to describe chemical and physical conditions in stars.-Early life:...
in 1920, and later (1923) by Irving Langmuir
Irving Langmuir
Irving Langmuir was an American chemist and physicist. His most noted publication was the famous 1919 article "The Arrangement of Electrons in Atoms and Molecules" in which, building on Gilbert N. Lewis's cubical atom theory and Walther Kossel's chemical bonding theory, he outlined his...
. One of the important applications of the equation was in explaining the spectral classification of stars. The equation is a result of combining ideas of quantum mechanics and statistical mechanics.
For a gas at a high enough temperature, the thermal collisions of the atoms will ionize some of the atoms. One or more of the electrons that are normally bound to the atom in orbits around the atomic nucleus will be ejected from the atom and will form an electron gas that co-exists with the gas of atomic ions and neutral atoms. This state of matter is called a plasma
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
. The Saha equation describes the degree of ionization of this plasma as a function of the temperature, density, and ionization energies of the atoms. The Saha equation only holds for weakly ionized plasmas for which the Debye length
Debye length
In plasma physics, the Debye length , named after the Dutch physicist and physical chemist Peter Debye, is the scale over which mobile charge carriers screen out electric fields in plasmas and other conductors. In other words, the Debye length is the distance over which significant charge...
is large. This means that the "screening" of the coulomb charge of ions and electrons by other ions and electrons is negligible. The subsequent lowering of the ionization potentials and the "cutoff" of the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
is therefore also negligible.
For a gas composed of a single atomic species, the Saha equation is written:
where:
-
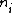is the density of atoms in the i-th state of ionization, that is with i electrons removed. -
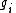is the degeneracyDegenerate energy levelIn physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
of states for the i-ions -
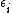is the energy required to remove i electrons from a neutral atom, creating an i-level ion. -
is the electron densityElectron densityElectron density is the measure of the probability of an electron being present at a specific location.In molecules, regions of electron density are usually found around the atom, and its bonds... -
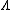is the thermal de Broglie wavelength of an electron
-
-
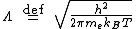
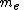is the mass of an electron -
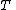is the temperatureTemperatureTemperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
of the gas -
is the Boltzmann constant -
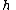is Planck's constant
-
In the case where only one level of ionization is important, we have
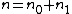and defining the total density n as , the Saha equation simplifies to: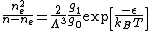where
is the energy of ionization.The Saha equation is useful for determining the ratio of particle densities for two different ionization levels. The most useful form of the Saha equation for this purpose is
,where Z denotes the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
. The Saha equation can be seen as a restatement of the equilibrium condition for the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
s:
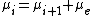
This equation simply states that the potential for an atom of ionization state i to ionize is the same as the potential for an electron and an atom of ionization state i+1; the potentials are equal, therefore the system is in equilibrium and no net change of ionization will occur.
In the early twenties Ralph H. Fowler
Ralph H. Fowler
Sir Ralph Howard Fowler OBE FRS was a British physicist and astronomer.-Education:Fowler was initially educated at home but then attended Evans' preparatory school at Horris Hill and Winchester College...
(in collaboration with Charles Galton Darwin
Charles Galton Darwin
Sir Charles Galton Darwin, KBE, MC, FRS was an English physicist, the grandson of Charles Darwin. He served as director of the National Physical Laboratory during the Second World War.-Early life:...
) developed a very powerful method in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
permitting a systematic exposition and working out of the equilibrium properties of matter. He used this to provide a (rigorous) derivation of the ionization formula which as described earlier Saha had obtained by extending (and justifiably) to ionization of atoms the theorem of Van 't Hoff
Jacobus Henricus van 't Hoff
Jacobus Henricus van 't Hoff, Jr. was a Dutch physical and organic chemist and the first winner of the Nobel Prize in chemistry. He is best known for his discoveries in chemical kinetics, chemical equilibrium, osmotic pressure, and stereochemistry...
, well known in physical chemistry for its application to molecular dissociation. Also, a significant improvement in the Saha equation introduced by Fowler was to include the effect of the excited states of atoms and ions. Further, it marked an important step forward when in 1923 Edward Arthur Milne and R.H. Fowler in a paper in the Monthly Notices of the Royal Astronomical Society showed that the criterion of the maximum intensity of absorption lines (belonging to subordinate series of a neutral atom) was much more fruitful in giving information about physical parameters of stellar atmospheres than the criterion employed by Saha which consisted in the marginal appearance or disappearance of absorption lines. (The latter criterion requires some knowledge of the relevant pressures in the stellar atmospheres, and Saha following the generally accepted view at the time assumed a value of the order of 1 to 0.1 atmosphere.) To quote from E. A. Milne:
"Saha had concentrated on the marginal appearances and disappearances of absorption lines in the stellar sequence, assuming an order of magnitude for the pressure in a stellar atmosphere and calculating the temperature where increasing ionization, for example, inhibited further absorption of the line in question owing to the loss of the series electron. As Fowler and I were one day stamping round my rooms in Trinity and discussing this, it suddenly occurred to me that the maximum intensity of the Balmer lines of hydrogenBalmer seriesThe Balmer series or Balmer lines in atomic physics, is the designation of one of a set of six different named series describing the spectral line emissions of the hydrogen atom....
, for example, was readily explained by the consideration that at the lower temperatures there were too few excited atoms to give appreciable absorption, whilst at the higher temperatures there are too few neutral atoms left to give any absorption. ..That evening I did a hasty order of magnitude calculation of the effect and found that to agree with a temperature of 10000° [K] for the stars of type A0, where the Balmer lines have their maximum, a pressure of the order of 10-4 atmosphere was required. This was very exciting, because standard determinations of pressures in stellar atmospheres from line shifts and line widths had been supposed to indicate a pressure of the order of one atmosphere or more, and I had begun on other grounds to disbelieve this."
External links
- Derivation & Discussion by Hale Bradt
- A detailed derivation from University of UtahUniversity of UtahThe University of Utah, also known as the U or the U of U, is a public, coeducational research university in Salt Lake City, Utah, United States. The university was established in 1850 as the University of Deseret by the General Assembly of the provisional State of Deseret, making it Utah's oldest...
Physics Department - Lecture notes from University of MarylandUniversity of Maryland, College ParkThe University of Maryland, College Park is a top-ranked public research university located in the city of College Park in Prince George's County, Maryland, just outside Washington, D.C...
Department of Astronomy - Saha, Megh Nad; On a Physical Theory of Stellar Spectra, Proceedings of the Royal Society of London, Series A, Volume 99, Issue 697 (May 1921), pp. 135–153
- Langmuir, Irving; and Kingdon, Kenneth H.; The Removal of Thorium from the Surface of a Thoriated Tungsten Filament by Positive Ion Bombardment, Physical Review, Vol. 22, No. 2 (August 1923), pp. 148–160