
Photon gas
Encyclopedia
In physics, a photon gas is a gas
-like collection of photon
s, which has many of the same properties of a conventional gas like hydrogen
or neon
- including pressure, temperature, and entropy. The most common example of a photon gas in equilibrium is black body radiation.
A massive ideal gas
with only one type of particle is uniquely described by three state functions such as the temperature
, volume
, and the number of particles
. However, for a black body, the energy distribution is established by the interaction of the photons with matter, usually the walls of the container. In this interaction, the number of photons is not conserved. As a result, the chemical potential
of the black body photon gas is zero. The number of state functions needed to describe a black body state is thus reduced from three to two (e.g. temperature and volume).
distribution at that temperature.
A very important difference between a gas of massive particles and a photon gas with a black body distribution is that the number of photons in the system is not conserved. A photon may collide with an electron in the wall, exciting it to a higher energy state, removing a photon from the photon gas. This electron may drop back to its lower level in a series of steps, each one of which releases an individual photon back into the photon gas. Although the sum of the energies of the emitted photons are the same as the absorbed photon, the number of emitted photons will vary. It can be shown that, as a result of this lack of constraint on the number of photons in the system, the chemical potential
of the photons must be zero for black body radiation.
The thermodynamics of a black body photon gas may be derived using quantum mechanical arguments
. The derivation yields the spectral energy distribution u which is the energy per unit volume per unit frequency interval:
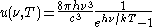
where h is Planck's constant, c is the speed of light, ν is the frequency, k is Boltzmann's constant, and T is temperature.
Integrating over frequency and multiplying by the volume (V ) gives the internal energy
of a black body photon gas: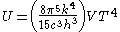
The derivation also yields the (expected) number of photons N:
where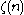 is the Riemann zeta function. Note that for a particular temperature, the particle number
is the Riemann zeta function. Note that for a particular temperature, the particle number
N varies with the volume in a fixed manner, adjusting itself to have a constant density of photons.
If we note that the equation of state for an ultra-relativistic quantum gas (which inherently describes photons) is given by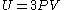
then we can combine the above formulas to produce an equation of state that looks much like that of an ideal gas: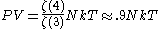
The following table summarizes the thermodynamic state functions for a black body photon gas.
|+ Thermodynamic state functions for a black body photon gas
|-
! align="center" |
! align="center" |State function (T,V)
|-
! align="center" |Internal energy
! align="center" |
|-
! align="center" |Particle number
! align="center" |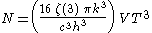
|-
! align="center" |Chemical potential
! align="center" |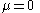
|-
! align="center" |Pressure
! align="center" |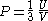
|-
! align="center" |Entropy
! align="center" |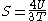
|-
! align="center" |Enthalpy
! align="center" |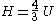
|-
! align="center" |Helmholtz free energy
! align="center" |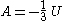
|-
! align="center" |Gibbs free energy
! align="center" |
|}

where the relationship V=Ax has been used. Defining

The pressure is
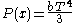
Integrating, the work done is just
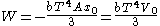
The amount of heat that must be added in order to create the gas is
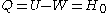
where H0 is the enthalpy at the end of the transformation. It is seen that the enthalpy is the amount of energy needed to create the photon gas.
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
-like collection of photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s, which has many of the same properties of a conventional gas like hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
or neon
Neon
Neon is the chemical element that has the symbol Ne and an atomic number of 10. Although a very common element in the universe, it is rare on Earth. A colorless, inert noble gas under standard conditions, neon gives a distinct reddish-orange glow when used in either low-voltage neon glow lamps or...
- including pressure, temperature, and entropy. The most common example of a photon gas in equilibrium is black body radiation.
A massive ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
with only one type of particle is uniquely described by three state functions such as the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
, and the number of particles
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
. However, for a black body, the energy distribution is established by the interaction of the photons with matter, usually the walls of the container. In this interaction, the number of photons is not conserved. As a result, the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
of the black body photon gas is zero. The number of state functions needed to describe a black body state is thus reduced from three to two (e.g. temperature and volume).
Thermodynamics of a black body photon gas
In a gas with massive particles, the energy of the particles is distributed according to a Maxwell-Boltzmann distribution. This distribution is established as the particles collide with each other, exchanging energy (and momentum) in the process. In a photon gas, there will also be an equilibrium distribution, but photons do not collide with each other (except under very extreme conditions) so that the equilibrium distribution must be established by other means. The most common way that an equilibrium distribution is established is by the interaction of the photons with matter. If the photons are absorbed and emitted by the walls of the system containing the photon gas, and the walls are at a particular temperature, then the equilibrium distribution for the photons will be a black bodyBlack body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
distribution at that temperature.
A very important difference between a gas of massive particles and a photon gas with a black body distribution is that the number of photons in the system is not conserved. A photon may collide with an electron in the wall, exciting it to a higher energy state, removing a photon from the photon gas. This electron may drop back to its lower level in a series of steps, each one of which releases an individual photon back into the photon gas. Although the sum of the energies of the emitted photons are the same as the absorbed photon, the number of emitted photons will vary. It can be shown that, as a result of this lack of constraint on the number of photons in the system, the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
of the photons must be zero for black body radiation.
The thermodynamics of a black body photon gas may be derived using quantum mechanical arguments
Gas in a box
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
. The derivation yields the spectral energy distribution u which is the energy per unit volume per unit frequency interval:
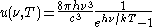
where h is Planck's constant, c is the speed of light, ν is the frequency, k is Boltzmann's constant, and T is temperature.
Integrating over frequency and multiplying by the volume (V ) gives the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of a black body photon gas:
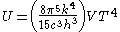
The derivation also yields the (expected) number of photons N:

where
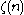 is the Riemann zeta function. Note that for a particular temperature, the particle number
is the Riemann zeta function. Note that for a particular temperature, the particle numberParticle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
N varies with the volume in a fixed manner, adjusting itself to have a constant density of photons.
If we note that the equation of state for an ultra-relativistic quantum gas (which inherently describes photons) is given by
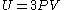
then we can combine the above formulas to produce an equation of state that looks much like that of an ideal gas:
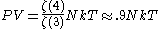
The following table summarizes the thermodynamic state functions for a black body photon gas.
-
-
- {| border="1" cellpadding="4" cellspacing="0" style="margin: 0 0 1em; border-color:#ccc"
-
|+ Thermodynamic state functions for a black body photon gas
|-
! align="center" |
! align="center" |State function (T,V)
|-
! align="center" |Internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
! align="center" |

|-
! align="center" |Particle number
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
! align="center" |
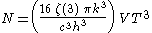
|-
! align="center" |Chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
! align="center" |
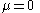
|-
! align="center" |Pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
! align="center" |
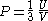
|-
! align="center" |Entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
! align="center" |
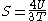
|-
! align="center" |Enthalpy
Enthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
! align="center" |
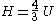
|-
! align="center" |Helmholtz free energy
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
! align="center" |
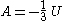
|-
! align="center" |Gibbs free energy
Gibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
! align="center" |

|}
Isothermal transformations
As an example of a thermodynamic process involving a photon gas, consider a cylinder with a movable piston. The interior walls of the cylinder are "black" in order that the temperature of the photons can be maintained at a particular temperature. This means that the space inside the cylinder will contain a blackbody-distributed photon gas. Unlike a massive gas, this gas will exist without the photons being introduced from the outside - the walls will provide the photons for the gas. Suppose the piston is pushed all the way into the cylinder so that there is an extremely small volume. The photon gas inside the volume will press against the piston, moving it outward, and in order for the transformation to be isothermic, a counter force of almost the same value will have to be applied to the piston so that the motion of the piston is very slow. This force will be equal to the pressure times the cross sectional area (A ) of the piston. This process can be continued at a constant temperature until the photon gas is at a volume V0 . Integrating the force over the distance (x ) traveled yields the total work done to create this photon gas at this volume
where the relationship V=Ax has been used. Defining

The pressure is
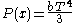
Integrating, the work done is just
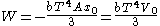
The amount of heat that must be added in order to create the gas is
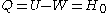
where H0 is the enthalpy at the end of the transformation. It is seen that the enthalpy is the amount of energy needed to create the photon gas.
See also
- PhotonPhotonIn physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
- Gas in a boxGas in a boxIn quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
- derivation of distribution functions for all ideal gases - Planck's law of black body radiationPlanck's law of black body radiationIn physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
- The distribution of photon energies as a function of frequency or wavelength. - Stefan-Boltzmann law - The total flux emitted by a black body.
- Radiation pressureRadiation pressureRadiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...

