
Product of rings
Encyclopedia
In mathematics
, it is possible to combine several rings
into one large product ring. This is done as follows: if I is some index set
and Ri is a ring for every i in I, then the cartesian product
Πi in I Ri can be turned into a ring by defining the operations coordinatewise, i.e. + (bi) = (ai + bi) · (bi) = (ai · bi)
The resulting ring is called a direct product of the rings Ri. The direct product of finitely many rings R1,...,Rk is also written as R1 × R2 × ... × Rk or R1 ⊕ R2 ⊕ ... ⊕ Rk, and can also be called the direct sum (and sometimes the complete direct sum) of the rings Ri.
s modulo
n. If n is written as a product of prime
powers (see fundamental theorem of arithmetic
):
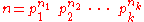
where the pi are distinct primes, then Z/nZ is naturally isomorphic to the product ring

This follows from the Chinese remainder theorem
.
pi: R → Ri which projects the product on the i-th coordinate. The product R, together with the projections pi, has the following universal property
:
This shows that the product of rings is an instance of products in the sense of category theory
. However, despite also being called the direct sum of rings when I is finite, the product of rings is not a coproduct
in the sense of category theory. In particular, if I has more than one element, the inclusion map Ri → R is not ring homomorphism as it does not map the identity in Ri to the identity in R.
If Ai in Ri is an ideal
for each i in I, then A = Πi in I Ai is an ideal of R. If I is finite, then the converse is true, i.e. every ideal of R is of this form. However, if I is infinite and the rings Ri are non-zero, then the converse is false; the set of elements with all but finitely many nonzero coordinates forms an ideal which is not a direct product of ideals of the Ri. The ideal A is a prime ideal
in R if all but one of the Ai are equal to Ri and the remaining Ai is a prime ideal in Ri. However, the converse is not true when I is infinite. For example, the direct sum
of the Ri form an ideal not contained in any such A, but the axiom of choice gives that it is contained in some maximal ideal
which is a fortiori prime.
An element x in R is a unit if and only if all of its components are units, i.e. if and only if pi(x) is a unit in Ri for every i in I. The group of units of R is the product
of the groups of units of Ri.
A product of more than one non-zero rings always has zero divisors: if x is an element of the product all of whose coordinates are zero except pi(x), and y is an element of the product with all coordinates zero except pj(y) (with i ≠ j), then xy = 0 in the product ring.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, it is possible to combine several rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
into one large product ring. This is done as follows: if I is some index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
and Ri is a ring for every i in I, then the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
Πi in I Ri can be turned into a ring by defining the operations coordinatewise, i.e. + (bi) = (ai + bi) · (bi) = (ai · bi)
The resulting ring is called a direct product of the rings Ri. The direct product of finitely many rings R1,...,Rk is also written as R1 × R2 × ... × Rk or R1 ⊕ R2 ⊕ ... ⊕ Rk, and can also be called the direct sum (and sometimes the complete direct sum) of the rings Ri.
Examples
An important example is the ring Z/nZ of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n. If n is written as a product of prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
powers (see fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
):
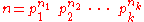
where the pi are distinct primes, then Z/nZ is naturally isomorphic to the product ring

This follows from the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
.
Properties
If R = Πi in I Ri is a product of rings, then for every i in I we have a surjective ring homomorphismRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
pi: R → Ri which projects the product on the i-th coordinate. The product R, together with the projections pi, has the following universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
:
- if S is any ring and fi: S → Ri is a ring homomorphism for every i in I, then there exists precisely one ring homomorphism f: S → R such that pi o f = fi for every i in I.
This shows that the product of rings is an instance of products in the sense of category theory
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
. However, despite also being called the direct sum of rings when I is finite, the product of rings is not a coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in the sense of category theory. In particular, if I has more than one element, the inclusion map Ri → R is not ring homomorphism as it does not map the identity in Ri to the identity in R.
If Ai in Ri is an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
for each i in I, then A = Πi in I Ai is an ideal of R. If I is finite, then the converse is true, i.e. every ideal of R is of this form. However, if I is infinite and the rings Ri are non-zero, then the converse is false; the set of elements with all but finitely many nonzero coordinates forms an ideal which is not a direct product of ideals of the Ri. The ideal A is a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
in R if all but one of the Ai are equal to Ri and the remaining Ai is a prime ideal in Ri. However, the converse is not true when I is infinite. For example, the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of the Ri form an ideal not contained in any such A, but the axiom of choice gives that it is contained in some maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
which is a fortiori prime.
An element x in R is a unit if and only if all of its components are units, i.e. if and only if pi(x) is a unit in Ri for every i in I. The group of units of R is the product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of the groups of units of Ri.
A product of more than one non-zero rings always has zero divisors: if x is an element of the product all of whose coordinates are zero except pi(x), and y is an element of the product with all coordinates zero except pj(y) (with i ≠ j), then xy = 0 in the product ring.

