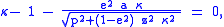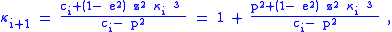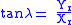Geodetic system
Encyclopedia
Geodetic systems or geodetic data are used in geodesy
, navigation
, surveying
by cartographers and satellite navigation systems to translate positions indicated on their products to their real position on earth
.
The systems are needed because the earth
is an imperfect sphere
. Also the earth is an imperfect ellipsoid. This can be verified by differentiating the equation for an ellipsoid and solving for dy/dx. It is a constant multiplied by x/y. Then derive the force equation from the centrifugal force acting on an object on the earth's surface and the gravitational force. Switch the x and y components and multiply one of them by negative one. This is the differential equation which when solved will yield the equation for the earth's surface. This is not a constant multiplied by x/y. Note that the earth's surface is also not an equal-potential surface, as can be verified by calculating the potential at the equator and the potential at a pole. The earth is an equal force surface. A one kilogram frictionless object on the ideal earth's surface does not have any force acting upon it to cause it to move either north or south. There is no simple analytical solution to this differential equation. A power series solution using three terms when substituted into this differential equation bogs down a TI-89 calculator and yields about three hundred terms after about five minutes.
The USGS uses a spherical harmonic expansion to approximate the earth's surface. It has about one hundred thousand terms. This problem has applications to moving Apollo asteroids. Some of them are loose rock and spinning. Their surface will be determined by the solution to this differential equation.
An interesting experiment will be to spin a mass of water in the space station and accurately measure its surface and do this for various angular velocities. Also, we can accurately measure Jupiter's surface using our telescopes. We can accurately determine earth's surface by using GPS.
Examples of map datums are:
The difference in co-ordinates between data is commonly referred to as datum shift. The datum shift between two particular datums can vary from one place to another within one country or region, and can be anything from zero to hundreds of metres (or several kilometres for some remote islands). The North Pole
, South Pole
and Equator
may be assumed to be in different positions on different datums, so True North
may be very slightly different. Different datums use different estimates for the precise shape and size of the Earth (reference ellipsoid
s).
The difference between WGS84 and OSGB36, for example, is up to 140 metres (450 feet), which for some navigational purposes is an insignificant error. For other applications, such as surveying
, or dive site location for SCUBA
divers, 140 metres is an unacceptably large error.
Because the Earth is an imperfect ellipsoid, localised datums can give a more accurate representation of the area of coverage than the global WGS 84 datum. OSGB36, for example, is a better approximation to the geoid
covering the British Isles than the global WGS 84 ellipsoid. However, as the benefits of a global system outweigh the greater accuracy, the global WGS 84 datum is becoming increasingly adopted.
and geodesy
, a datum is a reference point or surface against which position measurements are made, and an associated model of the shape of the earth for computing positions. Horizontal datums are used for describing a point on the earth
's surface, in latitude
and longitude
or another coordinate system. Vertical datums are used to measure elevations or underwater depths.
s of points on the Earth's surface. Vertical datums are either tidal, based on sea level
s, gravimetric, based on a geoid
, or geodetic, based on the same ellipsoid models of the earth used for computing horizontal datums.
In common usage, elevations are often cited in height above mean sea level; this is a widely used tidal datum. Mean Sea Level (MSL) is a tidal datum which is described as the arithmetic mean of the hourly water elevation taken over a specific 19 years cycle. This definition averages out tidal highs and lows due to the gravitational effects of the sun and the moon. MSL is defined as the zero elevation for a local area. However, zero elevation as defined by one country is not the same as zero elevation defined by another (because MSL is not the same everywhere). Which is why locally defined vertical datums differ from one another. Whilst the use of sea-level as a datum is useful for geologically recent topographic features, sea level has not stayed constant throughout geological time, so is less useful when measuring very long-term processes.
A geodetic vertical datum takes some specific zero point, and computes elevations based on the geodetic model being used, without further reference to sea levels. Usually, the starting reference point is a tide gauge, so at that point the geodetic and tidal datums might match, but due to sea level variations, the two scales may not match elsewhere. One example of a geoid
datum is NAVD88, used in North America, which is referenced to a point in Quebec
, Canada
.
 In geodetic coordinates the Earth's surface is approximated by an ellipsoid and locations near the surface are described in terms of latitude (
In geodetic coordinates the Earth's surface is approximated by an ellipsoid and locations near the surface are described in terms of latitude ( ), longitude (
), longitude ( ) and height (
) and height (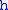 )About the right/left-handed order of the coordinates, i.e.,
)About the right/left-handed order of the coordinates, i.e., 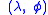 or
or  , see Spherical coordinate system#Conventions..
, see Spherical coordinate system#Conventions..
The ellipsoid is completely parameterised by the semi-major axis and the flattening
and the flattening  .
.
 ) is different from geocentric latitude (
) is different from geocentric latitude ( ). Geodetic latitude is determined by the angle between the normal
). Geodetic latitude is determined by the angle between the normal
of the spheroid and the plane of the equator, whereas geocentric latitude is determined around the centre (see figure). Unless otherwise specified latitude is geodetic latitude.
From a and f it is possible to derive the semi-minor axis b, first eccentricity e and second eccentricity e′ of the ellipsoid
AGD66 and AGD84 both use the parameters defined by Australian National Spheroid (see below)
Australian National Spheroid (ANS)
Geocentric Datum of Australia 1994 (GDA94) and Geocentric Datum of Australia 2000 (GDA2000)
Both GDA94 and GDA2000 use the parameters defined by GRS80 (see below)
Geodetic Reference System 1980 (GRS80)
see GDA Technical Manual document for more details; the value given above for the flattening is not exact.
World Geodetic System 1984 (WGS84)
The Global Positioning System (GPS) uses the World Geodetic System 1984 (WGS84) to determine the location of a point near the surface of the Earth.
see The official World Geodetic System 1984 document for more details.
A more comprehensive list of geodetic systems can be found here
(ECEF or ECF) or conventional terrestrial coordinate system rotates with the Earth and has its origin at the centre of the Earth. The axis passes through the equator at the prime meridian. The
axis passes through the equator at the prime meridian. The  axis passes through the north pole but it does not exactly coincide with the instantaneous Earth rotational axis. The
axis passes through the north pole but it does not exactly coincide with the instantaneous Earth rotational axis. The  axis can be determined by the right-hand rule
axis can be determined by the right-hand rule
to be passing through the equator at 90o longitude.
 , the north
, the north  and the up
and the up  .
.
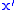 , the east
, the east 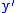 and the down
and the down 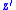 . To avoid confusion between
. To avoid confusion between  and
and  , etc. in this web page we will restrict the local coordinate frame to ENU.
, etc. in this web page we will restrict the local coordinate frame to ENU.
 , longitude
, longitude  , height
, height  ) can be converted into ECEF
) can be converted into ECEF
coordinates using the
following formulae:
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
, navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
, surveying
Surveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
by cartographers and satellite navigation systems to translate positions indicated on their products to their real position on earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
.
The systems are needed because the earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is an imperfect sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. Also the earth is an imperfect ellipsoid. This can be verified by differentiating the equation for an ellipsoid and solving for dy/dx. It is a constant multiplied by x/y. Then derive the force equation from the centrifugal force acting on an object on the earth's surface and the gravitational force. Switch the x and y components and multiply one of them by negative one. This is the differential equation which when solved will yield the equation for the earth's surface. This is not a constant multiplied by x/y. Note that the earth's surface is also not an equal-potential surface, as can be verified by calculating the potential at the equator and the potential at a pole. The earth is an equal force surface. A one kilogram frictionless object on the ideal earth's surface does not have any force acting upon it to cause it to move either north or south. There is no simple analytical solution to this differential equation. A power series solution using three terms when substituted into this differential equation bogs down a TI-89 calculator and yields about three hundred terms after about five minutes.
The USGS uses a spherical harmonic expansion to approximate the earth's surface. It has about one hundred thousand terms. This problem has applications to moving Apollo asteroids. Some of them are loose rock and spinning. Their surface will be determined by the solution to this differential equation.
An interesting experiment will be to spin a mass of water in the space station and accurately measure its surface and do this for various angular velocities. Also, we can accurately measure Jupiter's surface using our telescopes. We can accurately determine earth's surface by using GPS.
Examples of map datums are:
- WGS 84, 72, 64 and 60 of the World Geodetic SystemWorld Geodetic SystemThe World Geodetic System is a standard for use in cartography, geodesy, and navigation. It comprises a standard coordinate frame for the Earth, a standard spheroidal reference surface for raw altitude data, and a gravitational equipotential surface that defines the nominal sea level.The latest...
- NAD83, the North American DatumNorth American DatumThe North American Datum is the official datum used for the primary geodetic network in North America.In the fields of cartography and land-use there are currently two North American Datums in use: the North American Datum of 1927 and the North American Datum of 1983...
which is very similar to WGS84 - NAD27, the older North American DatumNorth American DatumThe North American Datum is the official datum used for the primary geodetic network in North America.In the fields of cartography and land-use there are currently two North American Datums in use: the North American Datum of 1927 and the North American Datum of 1983...
, of which NAD83 was basically a readjustment http://www.ngs.noaa.gov/TOOLS/Nadcon/Nadcon.html - OSGB36 of the Ordnance SurveyOrdnance SurveyOrdnance Survey , an executive agency and non-ministerial government department of the Government of the United Kingdom, is the national mapping agency for Great Britain, producing maps of Great Britain , and one of the world's largest producers of maps.The name reflects its creation together with...
of Great BritainGreat BritainGreat Britain or Britain is an island situated to the northwest of Continental Europe. It is the ninth largest island in the world, and the largest European island, as well as the largest of the British Isles... - ED50ED50ED 50 is a geodetic datum which was defined after World War II for the international connection of geodetic networks....
, the European Datum
The difference in co-ordinates between data is commonly referred to as datum shift. The datum shift between two particular datums can vary from one place to another within one country or region, and can be anything from zero to hundreds of metres (or several kilometres for some remote islands). The North Pole
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...
, South Pole
South Pole
The South Pole, also known as the Geographic South Pole or Terrestrial South Pole, is one of the two points where the Earth's axis of rotation intersects its surface. It is the southernmost point on the surface of the Earth and lies on the opposite side of the Earth from the North Pole...
and Equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
may be assumed to be in different positions on different datums, so True North
True north
True north is the direction along the earth's surface towards the geographic North Pole.True geodetic north usually differs from magnetic north , and from grid north...
may be very slightly different. Different datums use different estimates for the precise shape and size of the Earth (reference ellipsoid
Reference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
s).
The difference between WGS84 and OSGB36, for example, is up to 140 metres (450 feet), which for some navigational purposes is an insignificant error. For other applications, such as surveying
Surveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
, or dive site location for SCUBA
Scuba set
A scuba set is an independent breathing set that provides a scuba diver with the breathing gas necessary to breathe underwater during scuba diving. It is much used for sport diving and some sorts of work diving....
divers, 140 metres is an unacceptably large error.
Because the Earth is an imperfect ellipsoid, localised datums can give a more accurate representation of the area of coverage than the global WGS 84 datum. OSGB36, for example, is a better approximation to the geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
covering the British Isles than the global WGS 84 ellipsoid. However, as the benefits of a global system outweigh the greater accuracy, the global WGS 84 datum is becoming increasingly adopted.
Datum
In surveyingSurveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
and geodesy
Geodesy
Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
, a datum is a reference point or surface against which position measurements are made, and an associated model of the shape of the earth for computing positions. Horizontal datums are used for describing a point on the earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
's surface, in latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
and longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
or another coordinate system. Vertical datums are used to measure elevations or underwater depths.
Horizontal datums
The horizontal datum is the model used to measure positions on the earth. A specific point on the earth can have substantially different coordinates, depending on the datum used to make the measurement. There are hundreds of locally-developed horizontal datums around the world, usually referenced to some convenient local reference point. Contemporary datums, based on increasingly accurate measurements of the shape of the earth, are intended to cover larger areas. The WGS 84 datum, which is almost identical to the NAD83 datum used in North America and the ETRS89 datum used in Europe, is a common standard datum.Vertical datum
A vertical datum is used for measuring the elevationElevation
The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....
s of points on the Earth's surface. Vertical datums are either tidal, based on sea level
Sea level
Mean sea level is a measure of the average height of the ocean's surface ; used as a standard in reckoning land elevation...
s, gravimetric, based on a geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
, or geodetic, based on the same ellipsoid models of the earth used for computing horizontal datums.
In common usage, elevations are often cited in height above mean sea level; this is a widely used tidal datum. Mean Sea Level (MSL) is a tidal datum which is described as the arithmetic mean of the hourly water elevation taken over a specific 19 years cycle. This definition averages out tidal highs and lows due to the gravitational effects of the sun and the moon. MSL is defined as the zero elevation for a local area. However, zero elevation as defined by one country is not the same as zero elevation defined by another (because MSL is not the same everywhere). Which is why locally defined vertical datums differ from one another. Whilst the use of sea-level as a datum is useful for geologically recent topographic features, sea level has not stayed constant throughout geological time, so is less useful when measuring very long-term processes.
A geodetic vertical datum takes some specific zero point, and computes elevations based on the geodetic model being used, without further reference to sea levels. Usually, the starting reference point is a tide gauge, so at that point the geodetic and tidal datums might match, but due to sea level variations, the two scales may not match elsewhere. One example of a geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
datum is NAVD88, used in North America, which is referenced to a point in Quebec
Quebec
Quebec or is a province in east-central Canada. It is the only Canadian province with a predominantly French-speaking population and the only one whose sole official language is French at the provincial level....
, Canada
Canada
Canada is a North American country consisting of ten provinces and three territories. Located in the northern part of the continent, it extends from the Atlantic Ocean in the east to the Pacific Ocean in the west, and northward into the Arctic Ocean...
.
Geodetic coordinates

 ), longitude (
), longitude ( ) and height (
) and height (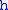 )About the right/left-handed order of the coordinates, i.e.,
)About the right/left-handed order of the coordinates, i.e., 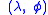 or
or  , see Spherical coordinate system#Conventions..
, see Spherical coordinate system#Conventions..The ellipsoid is completely parameterised by the semi-major axis
 and the flattening
and the flattening  .
.Geodetic versus geocentric latitude
It is important to note that geodetic latitude ( ) is different from geocentric latitude (
) is different from geocentric latitude ( ). Geodetic latitude is determined by the angle between the normal
). Geodetic latitude is determined by the angle between the normalSurface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
of the spheroid and the plane of the equator, whereas geocentric latitude is determined around the centre (see figure). Unless otherwise specified latitude is geodetic latitude.
Defining and derived parameters
| Parameter | Symbol |
|---|---|
| Semi-major axis | a |
| Reciprocal of flattening | 1/f |
From a and f it is possible to derive the semi-minor axis b, first eccentricity e and second eccentricity e′ of the ellipsoid
| Parameter | Value |
|---|---|
| semi-minor axis | b = a(1-f) |
| First eccentricity squared | e2 = 1-b2/a2 = 2f-f2 |
| Second eccentricity | e′2 = a2/b2 - 1 = f(2-f)/(1-f)2 |
Parameters for some geodetic systems
Australian Geodetic Datum 1966 [AGD66] and Australian Geodetic Datum 1984 (GDA84)AGD66 and AGD84 both use the parameters defined by Australian National Spheroid (see below)
Australian National Spheroid (ANS)
| Parameter | Notation | Value |
|---|---|---|
| semi-major axis | a | 6378160.000 m |
| Reciprocal of Flattening | 1/f | 298.25 |
Geocentric Datum of Australia 1994 (GDA94) and Geocentric Datum of Australia 2000 (GDA2000)
Both GDA94 and GDA2000 use the parameters defined by GRS80 (see below)
Geodetic Reference System 1980 (GRS80)
| Parameter | Notation | Value |
|---|---|---|
| semi-major axis | a | 6378137 m |
| Reciprocal of flattening | 1/f | 298.257222101 |
see GDA Technical Manual document for more details; the value given above for the flattening is not exact.
World Geodetic System 1984 (WGS84)
The Global Positioning System (GPS) uses the World Geodetic System 1984 (WGS84) to determine the location of a point near the surface of the Earth.
| Parameter | Notation | Value |
|---|---|---|
| semi-major axis | a | 6378137.0 m |
| Reciprocal of flattening | 1/f | 298.257223563 |
| Constant | Notation | Value |
|---|---|---|
| Semi-minor axis | b | 6356752.3142 m |
| First Eccentricity Squared | e2 | 6.69437999014x10−3 |
| Second Eccentricity Squared | e′2 | 6.73949674228x10−3 |
see The official World Geodetic System 1984 document for more details.
A more comprehensive list of geodetic systems can be found here
Other Earth-based coordinate systems
Earth-centred earth-fixed (ECEF or ECF) coordinates
The Earth-centered earth-fixedECEF
ECEF stands for Earth-Centered, Earth-Fixed, and is a Cartesian coordinate system, and is sometimes known as a "conventional terrestrial" system. It represents positions as an X, Y, and Z coordinate. The point is defined as the center of mass of the earth, hence the name Earth-Centered...
(ECEF or ECF) or conventional terrestrial coordinate system rotates with the Earth and has its origin at the centre of the Earth. The
 axis passes through the equator at the prime meridian. The
axis passes through the equator at the prime meridian. The  axis passes through the north pole but it does not exactly coincide with the instantaneous Earth rotational axis. The
axis passes through the north pole but it does not exactly coincide with the instantaneous Earth rotational axis. The  axis can be determined by the right-hand rule
axis can be determined by the right-hand ruleRight-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
to be passing through the equator at 90o longitude.
Local east, north, up (ENU) coordinates
In many targeting and tracking applications the local East, North, Up (ENU) Cartesian coordinate system is far more intuitive and practical than ECEF or Geodetic coordinates. The local ENU coordinates are formed from a plane tangent to the Earth's surface fixed to a specific location and hence it is sometimes known as a "Local Tangent" or "local geodetic" plane. By convention the east axis is labeled , the north
, the north  and the up
and the up  .
.Local north, east, down (NED) coordinates
In an airplane most objects of interest are below you, so it is sensible to define down as a positive number. The NED coordinates allow you to do this as an alternative to the ENU local tangent plane. By convention the north axis is labeled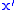 , the east
, the east 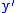 and the down
and the down 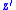 . To avoid confusion between
. To avoid confusion between  and
and  , etc. in this web page we will restrict the local coordinate frame to ENU.
, etc. in this web page we will restrict the local coordinate frame to ENU.From geodetic to ECEF
Geodetic coordinates (latitude , longitude
, longitude  , height
, height  ) can be converted into ECEF
) can be converted into ECEFECEF
ECEF stands for Earth-Centered, Earth-Fixed, and is a Cartesian coordinate system, and is sometimes known as a "conventional terrestrial" system. It represents positions as an X, Y, and Z coordinate. The point is defined as the center of mass of the earth, hence the name Earth-Centered...
coordinates using the
following formulae:
-

where-

 and
and  are the semi-major axis and the square of the first numerical eccentricity of the ellipsoid respectively.
are the semi-major axis and the square of the first numerical eccentricity of the ellipsoid respectively.
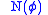 is called the Normal and is the distance from the surface to the Z-axis along the ellipsoid normal.
is called the Normal and is the distance from the surface to the Z-axis along the ellipsoid normal.
From ECEF to geodetic
The conversion of ECEF coordinates to geodetic coordinates (such WGS84) is a much harder problem, except for longitude, .
.
There exist two kinds of methods in order to solve the equation.
Newton-Raphson method
The following Bowring's irrational geodetic equation is efficient to be solved by Newton–Raphson iteration method:
where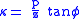 and
and 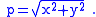
The iteration can be transformed into the following calculation:
where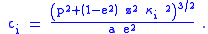
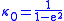 is a good starter for the iteration when
is a good starter for the iteration when  . Bowring showed that the single iteration produces the sufficiently accurate solution. He used trigonometric functions in his original formulation.
. Bowring showed that the single iteration produces the sufficiently accurate solution. He used trigonometric functions in his original formulation.
Ferrari's solution
The following solve the above equation:-

ECEF to/from ENU coordinates
To convert from geodetic coordinates to local ENU up coordinates is a two stage process- Convert geodetic coordinates to ECEF coordinates
- Convert ECEF coordinates to local ENU coordinates
To convert from local ENU up coordinates to geodetic coordinates is a two stage process- Convert local ENU coordinates to ECEF coordinates
- Convert ECEF coordinates to geodetic coordinates
From ECEF to ENU
To transform from ECEF coordinates to the local coordinates we need a local reference point, typically this might be the location of a radar. If a radar is located at and an aircraft at
and an aircraft at 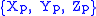 then the vector pointing from the radar to the aircraft in the ENU frame is
then the vector pointing from the radar to the aircraft in the ENU frame is
-

Note: is the geodetic latitude. A prior version of this page showed use of the geocentric latitude (
is the geodetic latitude. A prior version of this page showed use of the geocentric latitude (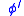 ). The geocentric latitude is not the appropriate up direction for the local tangent plane. If the original geodetic latitude is available it should be used, otherwise, the relationship between geodetic and geocentric latitude has an altitude dependency, and is captured by:
). The geocentric latitude is not the appropriate up direction for the local tangent plane. If the original geodetic latitude is available it should be used, otherwise, the relationship between geodetic and geocentric latitude has an altitude dependency, and is captured by:

Obtaining geodetic latitude from geocentric coordinates from this relationship requires an iterative solution approach, otherwise the geodetic coordinates may be computed via the approach in the section below labeled "From ECEF to geodetic coordinates."
The geocentric and geodetic longitude have the same value. This is true for the Earth and other similar shaped planets because their latitude lines (parallels) can be considered in much more degree perfect circles when compared to their longitude lines (meridians).
Note: Unambiguous determination of and
and  requires knowledge of which quadrant the coordinates lie in.
requires knowledge of which quadrant the coordinates lie in.
From ENU to ECEF
This is just the inversion of the ECEF to ENU transformation so
-
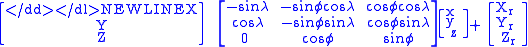
External links
- GeographicLib includes a utility CartConvert which converts between geodetic and geocentric (ECEFECEFECEF stands for Earth-Centered, Earth-Fixed, and is a Cartesian coordinate system, and is sometimes known as a "conventional terrestrial" system. It represents positions as an X, Y, and Z coordinate. The point is defined as the center of mass of the earth, hence the name Earth-Centered...
) or local Cartesian (ENU) coordinates. This provides accurate results for all inputs including points close to the center of the earth. - A collection of geodetic functions that solve a variety of problems in geodesy in Matlab.
Reference material
- List of geodetic parameters for many systems
- Kaplan, Understanding GPS: principles and applications, 1 ed. Norwood, MA 02062, USA: Artech House, Inc, 1996.
- GPS Notes
- Introduction to GPS Applications
- P. Misra and P. Enge, Global Positioning System Signals, Measurements, and Performance. Lincoln, Massachusetts: Ganga-Jamuna Press, 2001.
- Peter H. Dana: Geodetic Datum Overview - Large amount of technical information and discussion.
- UK Ordnance Survey
- US National Geodetic Survey
See also
- World Geodetic SystemWorld Geodetic SystemThe World Geodetic System is a standard for use in cartography, geodesy, and navigation. It comprises a standard coordinate frame for the Earth, a standard spheroidal reference surface for raw altitude data, and a gravitational equipotential surface that defines the nominal sea level.The latest...
- Ordnance DatumOrdnance DatumIn the British Isles, an Ordnance Datum or OD is a vertical datum used by an ordnance survey as the basis for deriving altitudes on maps. A spot height may be expressed as AOD for "above ordnance datum". Usually mean sea level is used for the datum...
- ECEFECEFECEF stands for Earth-Centered, Earth-Fixed, and is a Cartesian coordinate system, and is sometimes known as a "conventional terrestrial" system. It represents positions as an X, Y, and Z coordinate. The point is defined as the center of mass of the earth, hence the name Earth-Centered...
- GeographicLib includes a utility CartConvert which converts between geodetic and geocentric (ECEF
-
-
-