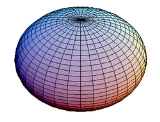
Spheroid
Encyclopedia
 |
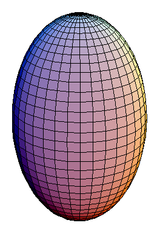 |
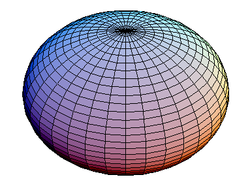
| oblate spheroid | prolate spheroid |
A spheroid, or ellipsoid of revolution is a quadric
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
obtained by rotating an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters.
If the ellipse is rotated about its major axis, the result is a prolate
Prolate spheroid
A prolate spheroid is a spheroid in which the polar axis is greater than the equatorial diameter. Prolate spheroids stand in contrast to oblate spheroids...
(elongated) spheroid, like a rugby
Rugby football
Rugby football is a style of football named after Rugby School in the United Kingdom. It is seen most prominently in two current sports, rugby league and rugby union.-History:...
ball. If the ellipse is rotated about its minor axis, the result is an oblate (flattened) spheroid, like a lentil
Lentil
The lentil is an edible pulse. It is a bushy annual plant of the legume family, grown for its lens-shaped seeds...
. If the generating ellipse is a circle, the result is a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
.
Because of the combined effects of gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
and rotation, the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
's shape is roughly that of a sphere slightly flattened in the direction of its axis. For that reason, in cartography
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
the Earth is often approximated by an oblate spheroid instead of a sphere. The current World Geodetic System
World Geodetic System
The World Geodetic System is a standard for use in cartography, geodesy, and navigation. It comprises a standard coordinate frame for the Earth, a standard spheroidal reference surface for raw altitude data, and a gravitational equipotential surface that defines the nominal sea level.The latest...
model uses a spheroid whose radius is 6,378.137 km at the equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
and 6,356.752 km at the pole
Geographical pole
A geographical pole is either of the two points—the north pole and the south pole—on the surface of a rotating planet where the axis of rotation meets the surface of the body...
s.
Equation
A spheroid centered at the "y" origin and rotated about the z axis is defined by the implicitImplicit function
The implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...
equation

where a is the horizontal, transverse radius at the equator, and b is the vertical, conjugate radius.
Surface area
A prolate spheroid has surface areaSurface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
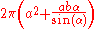
where
 is the angular eccentricity
is the angular eccentricityAngular eccentricity
In the study of ellipses and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening and eccentricity....
of the prolate spheroid, and
 is its (ordinary) eccentricity
is its (ordinary) eccentricityEccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
.
An oblate spheroid has surface area
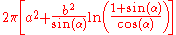 where
where  is the angular eccentricity
is the angular eccentricityAngular eccentricity
In the study of ellipses and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening and eccentricity....
of the oblate spheroid.
Volume
The volume of a spheroid (of any kind) is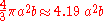 . If A=2a is the equatorial diameter, and B=2b is the polar diameter, the volume is
. If A=2a is the equatorial diameter, and B=2b is the polar diameter, the volume is 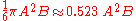 .
.Curvature
If a spheroid is parameterized as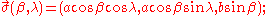
where
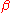 is the reduced or parametric latitude,
is the reduced or parametric latitude, 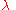 is the longitude
is the longitudeLongitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
, and
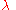
and
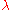 , then its Gaussian curvature
, then its Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
is

and its mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
is
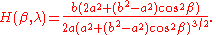
Both of these curvatures are always positive, so that every point on a spheroid is elliptic.

