Great-circle navigation
Encyclopedia
Great-circle navigation is the practice of navigating
a vessel (such as a ship
or aircraft
) along a track that follows a great circle
. A great circle track is the shortest distance between two points on the surface of a planetary body, assuming a perfect spherical model.
of a ship may employ several methods.
and this is plotted on the Mercator chart with the appropriate latitude
.
Spherical trigonometry
If a navigator begins at latitude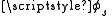 
(the "standpoint") and plans to travel the great circle to a point at latitude 
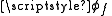(the "forepoint"), with a longitude difference between the points of 
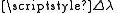(positive eastward), his initial course 
is given by
The central angle
between the two points,
, is given by
which involves the spherical law of cosines. The distance along the great circle will then be
times the assumed earth radius, where 
is in radians-- that is, degrees multiplied by 
.
The earth's actual radius of curvature varies by 1%, so this calculated distance might well be off by a few tenths of a percent; if that's not good enough the navigator can use the ellipsoid-surface formulas in the geographical distance
article.
Other formulas of spherical trigonometry give the latitudes at which the great circle crosses specified longitudes (or vice versa) or the lat-lons of points at specified distance intervals along the great circle.
plans to travel the great circle to a point at latitude 
, with a longitude difference between the points of L (positive eastward). His initial course 
is given by
The central angle
between the two points is given by
The distance along the great circle will then be
times the assumed earth radius, where 
is in radians-- that is, degrees multiplied by 
.
The earth's actual radius of curvature varies by 1%, so this calculated distance might well be off by a few tenths of a percent; if that's not good enough the navigator can use the ellipsoid-surface formulas in the geographical distance
article.
If the central angle is very close to zero or 180 degrees-- if the origin and destination are, say, a kilometer apart, or 19999 kilometers apart-- then the cosine of the central angle will be 0.99999999 or thereabouts, leading to some inaccuracy. The more complicated formulas above are intended to cover that situation and are otherwise unnecessary.
To find the lat-lons of points along the great circle, might as well first calculate the latitude and longitude of the vertex
where
is the difference in longitude between the navigator's starting point and the vertex. Then
The great circle crosses latitude
at longitude X east or west of the vertex. For example, if the vertex is at latitude 45 deg then the great circle crosses latitude 44 degrees at longitudes 15.05 deg east and west of the vertex. (All these formulas assume a spherical earth, of course; no chance formulas for the spheroid would be this simple.)
s which follow a great circle track. Normally, such programs will also calculate the total distance
, the distance between successive waypoints, and the courses to be followed between successive waypoints.
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
a vessel (such as a ship
Ship
Since the end of the age of sail a ship has been any large buoyant marine vessel. Ships are generally distinguished from boats based on size and cargo or passenger capacity. Ships are used on lakes, seas, and rivers for a variety of activities, such as the transport of people or goods, fishing,...
or aircraft
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air, or, in general, the atmosphere of a planet. An aircraft counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines.Although...
) along a track that follows a great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
. A great circle track is the shortest distance between two points on the surface of a planetary body, assuming a perfect spherical model.
Methods
In order to construct a great circle track, the navigatorNavigator
A navigator is the person on board a ship or aircraft responsible for its navigation. The navigator's primary responsibility is to be aware of ship or aircraft position at all times. Responsibilities include planning the journey, advising the Captain or aircraft Commander of estimated timing to...
of a ship may employ several methods.
Gnomonic chart
A straight line drawn on this chart would represent a great circle track. When this is transferred to a Mercator chart, it becomes a curve. The positions are transferred at a convenient interval of longitudeLongitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
and this is plotted on the Mercator chart with the appropriate latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
.
Spherical trigonometrySpherical trigonometrySpherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
If a navigator begins at latitude 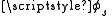(the "standpoint") and plans to travel the great circle to a point at latitude 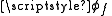(the "forepoint"), with a longitude difference between the points of 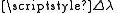(positive eastward), his initial course is given byThe central angle
Central angle
A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
between the two points,
, is given bywhich involves the spherical law of cosines. The distance along the great circle will then be
times the assumed earth radius, where is in radians-- that is, degrees multiplied by .The earth's actual radius of curvature varies by 1%, so this calculated distance might well be off by a few tenths of a percent; if that's not good enough the navigator can use the ellipsoid-surface formulas in the geographical distance
Geographical distance
Geographical distance is the distance measured along the surface of the earth. The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude and longitude.-An abstraction:...
article.
Other formulas of spherical trigonometry give the latitudes at which the great circle crosses specified longitudes (or vice versa) or the lat-lons of points at specified distance intervals along the great circle.
Spherical Trig (the simple version)
A navigator starting at latitude plans to travel the great circle to a point at latitude , with a longitude difference between the points of L (positive eastward). His initial course is given byThe central angle
Central angle
A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
between the two points is given by The distance along the great circle will then be
times the assumed earth radius, where is in radians-- that is, degrees multiplied by .The earth's actual radius of curvature varies by 1%, so this calculated distance might well be off by a few tenths of a percent; if that's not good enough the navigator can use the ellipsoid-surface formulas in the geographical distance
Geographical distance
Geographical distance is the distance measured along the surface of the earth. The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude and longitude.-An abstraction:...
article.
If the central angle is very close to zero or 180 degrees-- if the origin and destination are, say, a kilometer apart, or 19999 kilometers apart-- then the cosine of the central angle will be 0.99999999 or thereabouts, leading to some inaccuracy. The more complicated formulas above are intended to cover that situation and are otherwise unnecessary.
To find the lat-lons of points along the great circle, might as well first calculate the latitude and longitude of the vertex
where
is the difference in longitude between the navigator's starting point and the vertex. ThenThe great circle crosses latitude
at longitude X east or west of the vertex. For example, if the vertex is at latitude 45 deg then the great circle crosses latitude 44 degrees at longitudes 15.05 deg east and west of the vertex. (All these formulas assume a spherical earth, of course; no chance formulas for the spheroid would be this simple.)Computer software
Software is available that allows a navigator to input a departure ("standpoint") and arrival ("forepoint") position to create a list of waypointWaypoint
A waypoint is a reference point in physical space used for purposes of navigation.-Concept:Waypoints are sets of coordinates that identify a point in physical space. Coordinates used can vary depending on the application. For terrestrial navigation these coordinates can include longitude and...
s which follow a great circle track. Normally, such programs will also calculate the total distance
Great-circle distance
The great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
, the distance between successive waypoints, and the courses to be followed between successive waypoints.
Resources
- Great Circle – from MathWorld Great Circle description, figures, and equations. Mathworld, Wolfram Research, Inc. c1999
- Great Circle Mapper Interactive tool for plotting great circle routes.
- Great Circle Calculator deriving (initial) course and distance between two points.
- Great Circle Distance Graphical tool for drawing great circles over maps. Also shows distance and azimuth in a table.