In graph theory

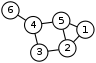
Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a graph property or graph invariant is a property of graphs

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 that depends only on the abstract structure, not on graph representations such as particular labellings

Graph labeling

In the mathematical discipline of graph theory, a graph labeling is the assignment of labels, traditionally represented by integers, to the edges or vertices, or both, of a graph....

 or drawings

Graph drawing

Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...

 of the graph.

Definitions

While graph drawing and graph representation are valid topics in graph theory, in order to focus only on the abstract structure of graphs, a graph property is defined to be a property preserved under all possible isomorphism

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

s of a graph. In other words, it is a property of the graph itself, not of a specific drawing or representation of the graph.

Informally, the term "graph invariant" is used for properties expressed quantitatively, while "property" usually refers to descriptive characterizations of graphs. For example, the statement "graph does not have vertices of degree 1" is a "property" while "the number of vertices of degree 1 in a graph" is an "invariant".

More formally, a graph property is a class of graphs, i.e. a function from graphs to {T,F}, and a graph invariant is a function from graphs to some other set, such as to the natural numbers (for scalar invariants), or to (possibly ordered) sequences of natural numbers (for properties like the degree sequence), or to a polynomial ring, such that isomorphic graphs have the same value.

A graph property is often called hereditary

Hereditary property

In mathematics, a hereditary property is a property of an object, that inherits to all its subobjects, where the term subobject depends on the context. These properties are particularly considered in topology and graph theory.-In topology:...

 if it also holds for (is "inherited" by) its induced subgraphs. A property is called additive if it is closed under disjoint union. The property of being planar

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

 is both hereditary and additive, for example, since a subgraph of a planar graph must be planar, and a disjoint union of two planar graphs must also be planar. The property of being connected

Connectivity (graph theory)

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...

 is neither, since a subgraph of a connected graph need not be connected, and a disjoint union of two connected graphs cannot be connected.

A graph property is sometimes called monotone increasing (or respectively monotone decreasing) if it is kept under the addition (respectively, the deletion) of edges. For example, the property of being connected

Connectivity (graph theory)

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...

 is clearly monotone increasing, whereas the property of being 3-colorable is monotone decreasing.

Graph invariants and graph isomorphism

Easily computable graph invariants are instrumental for fast recognition of graph isomorphism

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

, or rather non-isomorphism, since for any invariant at all, two graphs with different values cannot (by definition) be isomorphic. Two graphs with the same invariants may or may not be isomorphic, however.

A graph invariant I(G) is called complete if the identity of the invariants I(G) and I(H) implies the isomorphism of the graphs G and H. Finding such an invariant would imply an easy solution to the challenging graph isomorphism problem

Graph isomorphism problem

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.Besides its practical importance, the graph isomorphism problem is a curiosity in computational complexity theory as it is one of a very small number of problems belonging to NP...

. However, even polynomial-valued invariants such as the chromatic polynomial

Chromatic polynomial

The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...

 are not usually complete. The claw graph

Claw (graph theory)

In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.A claw is another name for the complete bipartite graph K1,3...

 and the path graph

Path graph

In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...

 on 4 vertices both have the same chromatic polynomial, for example.

Scalars

• order - the number of vertices
• size - the number of edges
• diameter
  Distance (graph theory)
  In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
  
   - the longest of the shortest path lengths between pairs of vertices
• girth - the length of the shortest cycle contained in the graph
• clustering coefficient
  Clustering coefficient
  In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...
  
  
• vertex connectivity
  Connectivity (graph theory)
  In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
  
   - the smallest number of vertices whose removal disconnects the graph
• edge connectivity - the smallest number of edges whose removal disconnects the graph
• independence number - the largest size of an independent set of vertices
• clique number - the largest order of a complete subgraph
• algebraic connectivity
  Algebraic connectivity
  The algebraic connectivity of a graph G is the second-smallest eigenvalue of the Laplacian matrix of G. This eigenvalue is greater than 0 if and only if G is a connected graph. This is a corollary to the fact that the number of times 0 appears as an eigenvalue in the Laplacian is the number of...
  
  
• vertex chromatic number - the minimum number of colors needed to color all vertices so that adjacent
  Adjacent
  Adjacent is an adjective meaning contiguous, adjoining or abuttingIn geometry, adjacent is when sides meet to make an angle.In graph theory adjacent nodes in a graph are linked by an edge....
  
   vertices have a different color
• edge chromatic number - the minimum number of colors needed to color all edges so that adjacent
  Adjacent
  Adjacent is an adjective meaning contiguous, adjoining or abuttingIn geometry, adjacent is when sides meet to make an angle.In graph theory adjacent nodes in a graph are linked by an edge....
  
   edges have a different color
• vertex covering number - the minimal number of vertices needed to cover all edges
• edge covering number - the minimal number of edges needed to cover all vertices
• isoperimetric number
  Cheeger constant (graph theory)
  In mathematics, the Cheeger constant of a graph is a numerical measure of whether or not a graph has a "bottleneck"...
  
  
• arboricity
  Arboricity
  The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned. Equivalently it is the minimum number of spanning forests needed to cover all the edges of the graph.-Example:...
  
  
• graph genus
• pagenumber
  Book embedding
  In graph theory, book embedding is a generalization of planar embedding to nonplanar surfaces in the form of a book, a collection of pages joined together at the spine of the book . The vertices of the graph are embedded on the spine, and each edge must lie in one of the pages...
  
  
• Hosoya index
  Hosoya index
  The Hosoya index, also known as the Z index, of a graph is the total number of matchings in it. The Hosoya index is always at least one, because the empty set of edges is counted as a matching for this purpose. Equivalently, the Hosoya index is the number of non-empty matchings plus...
  
  
• Wiener index
  Wiener index
  In chemical graph theory, the Wiener index is a topological index of a molecule, defined as the sum of the numbers of edges in the shortest paths in a chemical graph between all pairs of non-hydrogen atoms in a molecule. It was introduced by Harry Wiener in 1947. Wiener index may be calculated...
  
  
• Colin de Verdière graph invariant
  Colin de Verdière graph invariant
  Colin de Verdière's invariant is a graph parameter \mu for any graph G introduced by Yves Colin de Verdière in 1990. It was motivated by the study of the maximum multiplicity of the second eigenvalue of certain Schrödinger operators.-Definition:...
  
  
• boxicity
  Boxicity
  In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.The boxicity of a graph is the minimum dimension in which a given graph can be represented as an intersection graph of axis-parallel boxes...
  
  
• strength
  Strength of a graph (graph theory)
  In the branch of mathematics called graph theory, the strength of an undirected graph corresponds to the minimum ratio edges removed/components created in a decomposition of the graph in question...
  
  

Sequences and polynomials

• degree sequence
• graph spectrum
• characteristic polynomial
  Characteristic polynomial
  In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
  
   of the adjacency matrix
  Adjacency matrix
  In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
  
  
• chromatic polynomial
  Chromatic polynomial
  The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
  
   – the number of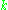 -colorings viewed as a function of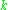
• Tutte polynomial
  Tutte polynomial
  The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
  
  – a bivariate function that encodes much of the graph’s connectivity