The algebraic connectivity of a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 G is the second-smallest eigenvalue of the Laplacian matrix

Laplacian matrix

In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...

 of G. This eigenvalue is greater than 0 if and only if G is a connected graph. This is a corollary to the fact that the number of times 0 appears as an eigenvalue in the Laplacian is the number of connected components in the graph. The magnitude of this value reflects how well connected the overall graph is, and has been used in analysing the synchronizability of networks.

Properties

The algebraic connectivity of a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 G is greater than 0 if and only if G is a connected graph. Furthermore, the value of the algebraic connectivity is bounded above by the traditional (vertex) connectivity

Connectivity (graph theory)

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...

 of the graph. If the number of vertices of a connected graph is n and the diameter

Distance (graph theory)

In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...

 is D, the algebraic connectivity is known to be bounded below by 1/nD, and in fact (in a result due to Brendan McKay

Brendan McKay

Brendan Damien McKay is a Professor in the Research School of Computer Science at the Australian National University . He has published extensively in combinatorics....

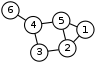
) by 4/nD. For the example shown above, for example, 4/18 = 0.222 ≤ 0.722 ≤ 1, but for many large graphs the algebraic connectivity is much closer to the lower bound than the upper.

Unlike the traditional connectivity, the algebraic connectivity is dependent on the number of vertices, as well as the way in which vertices are connected. In random graph

Random graph

In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...

s, the algebraic connectivity decreases with the number of vertices, and increases with the average degree

Degree (graph theory)

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...

.

The exact definition of the algebraic connectivity depends on the type of Laplacian used. Fan Chung

Fan Chung

Fan Rong K Chung Graham , known professionally as Fan Chung, is a mathematician who works mainly in the areas of spectral graph theory, extremal graph theory and random graphs, in particular...

 has developed an extensive theory using a rescaled version of the Laplacian, eliminating the dependence on the number of vertices, so that the bounds are somewhat different.

In models of synchronization

Synchronization

Synchronization is timekeeping which requires the coordination of events to operate a system in unison. The familiar conductor of an orchestra serves to keep the orchestra in time....

 on networks, such as the Kuramoto model

Kuramoto model

The Kuramoto model, first proposed by Yoshiki Kuramoto , is a mathematical model used to describe synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators...

, the Laplacian matrix arises naturally, and so the algebraic connectivity gives an indication of how easily the network will synchronize. However, other measures, such as the average distance

Distance (graph theory)

In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...

 (characteristic path length) can also be used, and in fact the algebraic connectivity is closely related to the (reciprocal of the) average distance.

The algebraic connectivity also relates to other connectivity attributes, such as the isoperimetric number, which is bounded below by half the algebraic connectivity.

The Fiedler vector

The original theory related to algebraic connectivity was produced by Miroslav Fiedler

Miroslav Fiedler

Miroslav Fiedler is a Czech mathematician known for his contributions tolinear algebra, graph theory and algebraic graph theory....

. In his honor the eigenvector associated with the algebraic connectivity has been named the Fiedler vector. The Fiedler vector can be used to partition

Graph partition

In mathematics, the graph partition problem is defined on data represented in the form of a graph G= , with V vertices and E edges, such that it is possible to partition G into smaller components with specific properties. For instance, a k-way partition divides the vertex set into k smaller...

 a graph.

For the example graph in the introductory section, the Fiedler vector is <0.415, 0.309, 0.069, −0.221, 0.221, −0.794>. The negative values are associated with the poorly connected vertex 6, and the neighbouring articulation point, vertex 4; while the positive values are associated with the other vertices. The signs of the values in the Fiedler vector can therefore be used to partition this graph into two components: {1, 2, 3, 5} and {4, 6}. Alternatively, the value of 0.069 (which is close to zero) can be placed in a class of its own, partitioning the graph into three components: {1, 2, 5}, {3}, and {4, 6}.