Graph isomorphism problem
Encyclopedia
The graph isomorphism problem is the computational problem
of determining whether two finite graph
s are isomorphic
.
Besides its practical importance, the graph isomorphism problem is a curiosity in computational complexity theory
as it is one of a very small number of problems belonging to NP
neither known to be solvable in polynomial time nor NP-complete
: it is one of only 12 such problems listed by , and one of only two of that list whose complexity remains unresolved (the other being integer factorization
). the best algorithm (Luks, 1983) has run time 2O(√(n log n)) for graphs with n vertices.
It is known that the graph isomorphism problem is in the low hierarchy of class NP, which implies that it is not NP-complete unless the polynomial time hierarchy collapses to its second level.
At the same time, isomorphism for many special classes of graphs can be solved in polynomial time, and in practice graph isomorphism can often be solved efficiently.
This problem is a special case of the subgraph isomorphism problem
, which is known to be NP-complete
. It is also known to be a special case of the non-abelian
hidden subgroup problem
over the symmetric group
.
. Without CFSG, a slightly weaker bound
2O(√n log2 n) was obtained first for strongly regular graph
s by László Babai
(1980), and then extended to general graphs by Babai & Luks (1982). Improvement of the exponent √n is a major open problem; for strongly regular graphs this was done by . For hypergraph
s of bounded rank, a subexponential upper bound matching the case of graphs, was recently obtained by .
On a side note, the graph isomorphism problem is computationally equivalent to the problem of computing the automorphism group of a graph, and is weaker than the permutation group
isomorphism problem, and the permutation group intersection problem. For the latter two problems, Babai, Kantor and Luks (1983) obtained complexity bounds similar to that for the graph isomorphism.
There are several competing practical algorithms for graph isomorphism, due to , , , etc. While they seem to perform well on random graphs, a major drawback of these algorithms is their exponential time performance in the worst case
.
.
As is common for complexity class
es within the polynomial time hierarchy, a problem is called GI-hard if there is a polynomial-time Turing reduction from any problem in GI to that problem, i.e., a polynomial-time solution to a GI-hard problem would yield a polynomial-time solution to the graph isomorphism problem (and so all problems in GI). A problem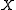
is called complete
for GI, or GI-complete, if it is both GI-hard and a polynomial-time solution to the GI problem would yield a polynomial-time solution to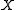
.
The graph isomorphism problem is contained in both NP and co-AM. GI is contained in and low
for Parity P, as well as contained in the potentially much smaller class SPP. That it lies in Parity P means that the graph isomorphism problem is no harder than determining whether a polynomial-time nondeterministic Turing machine has an even or odd number of accepting paths. GI is also contained in and low for ZPPNP. This essentially means that an efficient Las Vegas algorithm
with access to an NP oracle
can solve graph isomorphism so easily that it gains no power from being given the ability to do so in constant time.
Many classes of digraphs are also GI-complete.
and Kannan have shown a program checker for graph isomorphism. Suppose P is a claimed polynomial-time procedure that checks if two graphs are isomorphic, but it is not trusted. To check if G and H are isomorphic:
This procedure is polynomial-time and gives the correct answer if P is a correct program for graph isomorphism. If P is not a correct program, but answers correctly on G and H, the checker will either give the correct answer, or detect invalid behaviour of P.
If P is not a correct program, and answers incorrectly on G and H, the checker will detect invalid behaviour of P with high probability, or answer wrong with probability 2-100.
Notably, P is used only as a blackbox.
and in mathematical chemistry
, graph isomorphism testing is used to identify a chemical compound
within a chemical database
. Also, in organic mathematical chemistry graph isomorphism testing is useful for generation of molecular graph
s and for computer synthesis
.
Chemical database search is an example of graphical data mining
, where the graph canonization
approach is often used. In particular, a number of identifier
s for chemical substance
s, such as SMILES and InChI, designed to provide a standard and human-readable way to encode molecular information and to facilitate the search for such information in databases and on the web, use canonization step in their computation, which is essentially the canonization of the graph which represents the molecule.
In electronic design automation
graph isomorphism is the basis of the Layout Versus Schematic
(LVS) circuit design step, which is a verification whether the electric circuits represented by a circuit schematic
and an integrated circuit layout
are the same.
Computational problem
In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
of determining whether two finite graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s are isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
.
Besides its practical importance, the graph isomorphism problem is a curiosity in computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
as it is one of a very small number of problems belonging to NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
neither known to be solvable in polynomial time nor NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
: it is one of only 12 such problems listed by , and one of only two of that list whose complexity remains unresolved (the other being integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
). the best algorithm (Luks, 1983) has run time 2O(√(n log n)) for graphs with n vertices.
It is known that the graph isomorphism problem is in the low hierarchy of class NP, which implies that it is not NP-complete unless the polynomial time hierarchy collapses to its second level.
At the same time, isomorphism for many special classes of graphs can be solved in polynomial time, and in practice graph isomorphism can often be solved efficiently.
This problem is a special case of the subgraph isomorphism problem
Subgraph isomorphism problem
In theoretical computer science, the subgraph isomorphism problem is a computational task in which two graphs G and H are given as input, and one must determine whether G contains a subgraph that is isomorphic to H....
, which is known to be NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. It is also known to be a special case of the non-abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
hidden subgroup problem
Hidden subgroup problem
The hidden subgroup problem is a topic of research in mathematics and theoretical computer science.-Problem statement:Given a group G, a subgroup H ≤ G, and a set X, we say a function f : G → X hides the subgroup H if for all g1, g2 ∈ G,f = f if and only if g1H = g2H for the cosets of...
over the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
State of the art
The best current theoretical algorithm is due to Eugene Luks (1983), and is based on the earlier work by Luks (1981), Babai & Luks (1982), combined with a subfactorial algorithm due to Zemlyachenko (1982). The algorithm relies on the classification of finite simple groupsClassification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
. Without CFSG, a slightly weaker bound
2O(√n log2 n) was obtained first for strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
s by László Babai
László Babai
László Babai is a Hungarian professor of mathematics and computer science at the University of Chicago. His research focuses on computational complexity theory, algorithms, combinatorics, and finite groups, with an emphasis on the interactions between these fields...
(1980), and then extended to general graphs by Babai & Luks (1982). Improvement of the exponent √n is a major open problem; for strongly regular graphs this was done by . For hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s of bounded rank, a subexponential upper bound matching the case of graphs, was recently obtained by .
On a side note, the graph isomorphism problem is computationally equivalent to the problem of computing the automorphism group of a graph, and is weaker than the permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
isomorphism problem, and the permutation group intersection problem. For the latter two problems, Babai, Kantor and Luks (1983) obtained complexity bounds similar to that for the graph isomorphism.
There are several competing practical algorithms for graph isomorphism, due to , , , etc. While they seem to perform well on random graphs, a major drawback of these algorithms is their exponential time performance in the worst case
Best, worst and average case
In computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively...
.
Solved special cases
A number of important special cases of the graph isomorphism problem have efficient, polynomial-time solutions:- TreeTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
s - Planar graphPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s (In fact, planar graph isomorphism is in log spaceL (complexity)In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
, a class contained in PP (complexity)In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
.) - Interval graphInterval graphIn graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
s - Permutation graphPermutation graphIn areas of mathematics influenced by graph theory, a permutation graph is the intersection graph of a family of line segments that connect two parallel lines in the Euclidean plane...
s - Partial k-treeTree decompositionIn graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph...
s - Bounded-parameter graphs
- Graphs of bounded genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
(Note: planar graphs are graphs of genus 0) - Graphs of bounded degreeDegree (graph theory)In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
- Graphs with bounded eigenvalue multiplicity
- k-Contractible graphs (a generalization of bounded degree and bounded genus)
- Color-preserving isomorphism of colored graphs with bounded color multiplicity (i.e., at most k vertices have the same color for a fixed k) is in class NCNC (complexity)In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
, which is a subclass of PP (complexity)In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
.
- Graphs of bounded genus
Complexity class GI
Since the graph isomorphism problem is neither known to be NP-complete nor to be tractable, researchers have sought to gain insight into the problem by defining a new class GI, the set of problems with a polynomial-time Turing reduction to the graph isomorphism problem. If in fact the graph isomorphism problem is solvable in polynomial time, GI would equal PP (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
.
As is common for complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
es within the polynomial time hierarchy, a problem is called GI-hard if there is a polynomial-time Turing reduction from any problem in GI to that problem, i.e., a polynomial-time solution to a GI-hard problem would yield a polynomial-time solution to the graph isomorphism problem (and so all problems in GI). A problem
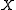is called completeComplete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
for GI, or GI-complete, if it is both GI-hard and a polynomial-time solution to the GI problem would yield a polynomial-time solution to
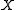.The graph isomorphism problem is contained in both NP and co-AM. GI is contained in and low
Low (complexity)
In computational complexity theory, a complexity class B is said to be low for a complexity class A if AB = A; that is, A with an oracle for B is equal to A. Such a statement implies that an abstract machine which solves problems in A achieves no additional power if it is given the ability to solve...
for Parity P, as well as contained in the potentially much smaller class SPP. That it lies in Parity P means that the graph isomorphism problem is no harder than determining whether a polynomial-time nondeterministic Turing machine has an even or odd number of accepting paths. GI is also contained in and low for ZPPNP. This essentially means that an efficient Las Vegas algorithm
Las Vegas algorithm
In computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. In other words, a Las Vegas algorithm does not gamble with the verity of the result; it gambles only with the resources...
with access to an NP oracle
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
can solve graph isomorphism so easily that it gains no power from being given the ability to do so in constant time.
Isomorphism of other objects
There are a number of classes of mathematical objects for which the problem of isomorphism is a GI-complete problem. A number of them are graphs endowed with additional properties or restrictions:- digraphsDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
- labelled graphs, with the proviso that an isomorphism is not required to preserve the labels, but only the equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
consisting of pairs of vertices with the same label - "polarized graphs" (made of a complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
Km and an empty graph Kn plus some edges connecting the two; their isomorphism must preserve the partition) - 2-colored graphs
- explicitly given finite structureStructure (mathematical logic)In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
s - multigraphMultigraphIn mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
s - hypergraphHypergraphIn mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s - finite automata
- Markov Decision ProcessesMarkov decision processMarkov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
- commutative class 3 nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
(i.e., xyz = 0 for every elements x, y, z) semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s - finite rank associative algebrasAlgebra over a fieldIn mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over a fixed algebraically closed field with zero squared radical and commutative factor over the radical - context-free grammarContext-free grammarIn formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
s - balanced incomplete block designs
- Recognizing combinatorial isomorphism of convex polytopeConvex polytopeA convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
s represented by vertex-facet incidences.
GI-complete classes of graphs
A class of graphs is called GI-complete if recognition of isomorphism for graphs from this subclass is a GI-complete problem. The following classes are GI-complete:- connected graphs
- graphs of diameter 2 and radius 1
- directed acyclic graphDirected acyclic graphIn mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
s - regular graphRegular graphIn graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
s. - bipartite graphBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s without non-trivial strongly regular subgraphsStrongly regular graphIn graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k... - bipartite Eulerian graphs
- bipartite regular graphs
- line graphLine graphIn graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
s - chordal graphChordal graphIn the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
s - regular self-complementary graphSelf-complementary graphA self-complementary graph is a graph which is isomorphic to its complement. The simplest non-trivial self-complementary graphs are the 4-vertex path graph and the 5-vertex cycle graph....
s - polytopal graphs of general, simpleSimple polytopeIn geometry, a d-dimensional simple polytope is a d-dimensional polytope each of whose vertices are adjacent to exactly d edges . The vertex figure of a simple d-polytope is a -simplex....
, and simplicialSimplicial polytopeIn geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
convex polytopeConvex polytopeA convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
s in arbitrary dimensions
Many classes of digraphs are also GI-complete.
Other GI-complete problems
There are other nontrivial GI-complete problems in addition to isomorphism problems.- The recognition of self-complementarity of a graph or digraph.
- A clique problemClique problemIn computer science, the clique problem refers to any of the problems related to finding particular complete subgraphs in a graph, i.e., sets of elements where each pair of elements is connected....
for a class of so-called M-graphs. It is shown that finding an isomorphism for n-vertex graphs is equivalent to finding an n-clique in an M-graph of size n2. This fact is interesting because the problem of finding an (n − ε)-clique in a M-graph of size n2 is NP-complete for arbitrarily small positive ε. - The problem of homeomorphism of 2-complexes.
GI-hard problems
- The problem of counting the number of isomorphisms between two graphs is polynomial-time equivalent to the problem of telling whether even one exists.
- The problem of deciding whether two convex polytopeConvex polytopeA convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
s given by either the V-description or H-description are projectively or affinely isomorphic. The latter means existence of a projective or affine map between the spaces that contain the two polytopes (not necessarily of the same dimension) which induces a bijection between the polytopes.
Program checking
BlumManuel Blum
Manuel Blum is a computer scientist who received the Turing Award in 1995 "In recognition of his contributions to the foundations of computational complexity theory and its application to cryptography and program checking".-Biography:Blum attended MIT, where he received his bachelor's degree and...
and Kannan have shown a program checker for graph isomorphism. Suppose P is a claimed polynomial-time procedure that checks if two graphs are isomorphic, but it is not trusted. To check if G and H are isomorphic:
- Ask P whether G and H are isomorphic.
- If the answer is "yes':
- Attempt to construct an isomorphism using P as subroutine. Mark a vertex u in G and v in H, and modify the graphs to make them distinctive (with a small local change). Ask P if the modified graphs are isomorphic. If no, change v to a different vertex. Continue searching.
- Either the isomorphism will be found (and can be verified), or P will contradict itself.
- If the answer if "no":
- Perform the following 100 times. Choose randomly G or H, and randomly permute its vertices. Ask P if the graph is isomorphic to G and H. (As in AM protocol for graph nonisomorphism).
- If any of the tests are failed, judge P as invalid program. Otherwise, answer "no".
- If the answer is "yes':
This procedure is polynomial-time and gives the correct answer if P is a correct program for graph isomorphism. If P is not a correct program, but answers correctly on G and H, the checker will either give the correct answer, or detect invalid behaviour of P.
If P is not a correct program, and answers incorrectly on G and H, the checker will detect invalid behaviour of P with high probability, or answer wrong with probability 2-100.
Notably, P is used only as a blackbox.
Applications
In cheminformaticsCheminformatics
Cheminformatics is the use of computer and informational techniques, applied to a range of problems in the field of chemistry. These in silico techniques are used in pharmaceutical companies in the process of drug discovery...
and in mathematical chemistry
Mathematical chemistry
Mathematical chemistry is the area of research engaged in novel applications of mathematics to chemistry; it concerns itself principally with the mathematical modeling of chemical phenomena...
, graph isomorphism testing is used to identify a chemical compound
Chemical compound
A chemical compound is a pure chemical substance consisting of two or more different chemical elements that can be separated into simpler substances by chemical reactions. Chemical compounds have a unique and defined chemical structure; they consist of a fixed ratio of atoms that are held together...
within a chemical database
Chemical database
A chemical database is a database specifically designed to store chemical information. This information is about chemical and crystal structures, spectra, reactions and syntheses, and thermophysical data.- Chemical structures :...
. Also, in organic mathematical chemistry graph isomorphism testing is useful for generation of molecular graph
Molecular graph
In chemical graph theory and in mathematical chemistry, a molecular graph or chemical graph is a representation of the structural formula of a chemical compound in terms of graph theory. A chemical graph is a labeled graph whose vertices correspond to the atoms of the compound and edges correspond...
s and for computer synthesis
Combinatorial chemistry
Combinatorial chemistry involves the rapid synthesis or the computer simulation of a large number of different but structurally related molecules or materials...
.
Chemical database search is an example of graphical data mining
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
, where the graph canonization
Graph canonization
In graph theory, a branch of mathematics, graph canonization is finding a canonical form of a graph G, which is a graph Canon isomorphic to G such that Canon = Canon if and only if H is isomorphic to G. The canonical form of a graph is an example of a complete graph invariant...
approach is often used. In particular, a number of identifier
Identifier
An identifier is a name that identifies either a unique object or a unique class of objects, where the "object" or class may be an idea, physical [countable] object , or physical [noncountable] substance...
s for chemical substance
Chemical substance
In chemistry, a chemical substance is a form of matter that has constant chemical composition and characteristic properties. It cannot be separated into components by physical separation methods, i.e. without breaking chemical bonds. They can be solids, liquids or gases.Chemical substances are...
s, such as SMILES and InChI, designed to provide a standard and human-readable way to encode molecular information and to facilitate the search for such information in databases and on the web, use canonization step in their computation, which is essentially the canonization of the graph which represents the molecule.
In electronic design automation
Electronic design automation
Electronic design automation is a category of software tools for designing electronic systems such as printed circuit boards and integrated circuits...
graph isomorphism is the basis of the Layout Versus Schematic
Layout versus schematic
The Layout Versus Schematic is the class of electronic design automation verification software that determines whether a particular integrated circuit layout corresponds to the original schematic or circuit diagram of the design.-Background:...
(LVS) circuit design step, which is a verification whether the electric circuits represented by a circuit schematic
Circuit diagram
A circuit diagram is a simplified conventional graphical representation of an electrical circuit...
and an integrated circuit layout
Integrated circuit layout
Integrated circuit layout, also known IC layout, IC mask layout, or mask design, is the representation of an integrated circuit in terms of planar geometric shapes which correspond to the patterns of metal, oxide, or semiconductor layers that make up the components of the integrated circuit.When...
are the same.
Surveys and monographs
- Ronald Read and Derek Corneil. "The graph isomorphism disease". Journal of Graph Theory 1977, 1, 339–363.
- Gati, G. "Further annotated bibliography on the isomorphism disease." – Journal of Graph Theory 1979, 3, 95–109.. (Translated from Zapiski Nauchnykh Seminarov Leningradskogo Otdeleniya Matematicheskogo Instituta im. V. A. Steklova AN SSSR (Records of Seminars of the Leningrad Department of Steklov Institute of Mathematics of the USSR Academy of Sciences), Vol. 118, pp. 83–158, 1982.). (A brief survey of open questions related to the isomorphism problem for graphs, rings and groups.). (From the book cover: The books focuses on the issue of the computational complexity of the problem and presents several recent results that provide a better understanding of the relative position of the problem in the class NP as well as in other complexity classes.). (This 24th edition of the Column discusses the state of the art for the open problems from the book Computers and Intractability and previous columns, in particular, for Graph Isomorphism.).
Software
- Graph Isomorphism, review of implementations, The Stony Brook Algorithm Repository.