
Strength of a graph (graph theory)
Encyclopedia
In the branch of mathematics
called graph theory
, the strength of an undirected graph
corresponds to the minimum ratio edges removed/components created in a decomposition of the graph in question. It is a method to compute partitions
of the set of vertices and detect zones of high concentration of edges.
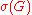 of an undirected simple graph G = (V, E) admits the three following definitions:
of an undirected simple graph G = (V, E) admits the three following definitions:
was discovered by Cunningham (1985). The algorithm with best complexity for computing exactly the strength is due to Trubin (1993), uses the flow decomposition of Goldberg and Rao (1998), in time .
.
necessarily balanced (i.e. of almost equal size).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
called graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the strength of an undirected graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
corresponds to the minimum ratio edges removed/components created in a decomposition of the graph in question. It is a method to compute partitions
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the set of vertices and detect zones of high concentration of edges.
Definitions
The strength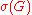 of an undirected simple graph G = (V, E) admits the three following definitions:
of an undirected simple graph G = (V, E) admits the three following definitions:- Let
 be the set of all partitionsPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
be the set of all partitionsPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of , and
, and  be the set of edges crossing over the sets of the partition
be the set of edges crossing over the sets of the partition  , then
, then 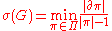 .
. - Also if
 is the set of all spanning trees of G, then
is the set of all spanning trees of G, then
-
-
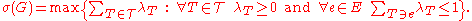
- And by linear programming duality,
-
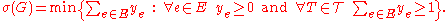
-
Complexity
Computing the strength of a graph can be done in polynomial time, and the first such algorithmwas discovered by Cunningham (1985). The algorithm with best complexity for computing exactly the strength is due to Trubin (1993), uses the flow decomposition of Goldberg and Rao (1998), in time
 .
.Properties
- If
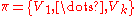 is one partition that maximizes, and for
is one partition that maximizes, and for 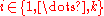 ,
, 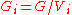 is the restriction of G to the set
is the restriction of G to the set 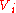 , then
, then  .
.
- The Tutte-Nash-Williams theorem:
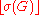 is the maximum number of edge-disjoint spanning trees that can be contained in G.
is the maximum number of edge-disjoint spanning trees that can be contained in G.
- Contrary to the graph partitionGraph partitionIn mathematics, the graph partition problem is defined on data represented in the form of a graph G= , with V vertices and E edges, such that it is possible to partition G into smaller components with specific properties. For instance, a k-way partition divides the vertex set into k smaller...
problem, the partitions output by computing the strength are not
necessarily balanced (i.e. of almost equal size).

