.gif)
Cheeger constant (graph theory)
Encyclopedia
In mathematics
, the Cheeger constant (also Cheeger number or isoperimetric number) of a graph
is a numerical measure of whether or not a graph has a "bottleneck". The Cheeger constant as a measure of "bottleneckedness" is of great interest in many areas: for example, constructing well-connected networks of computers, card shuffling, and low-dimensional topology
(in particular, the study of hyperbolic
3-manifold
s).
The Cheeger constant is named after the mathematician
Jeff Cheeger
.
be an undirected graph with vertex set 
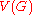and edge set 
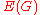. For a collection of vertices 
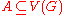, let 
denote the collection of all edges going from a vertex in 
to a vertex outside of 
:
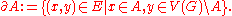
(Remember that edges are unordered, so the edge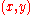
is the same as the edge 
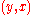.) Then the Cheeger constant of 
, denoted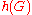 
, is defined by
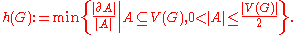
The Cheeger constant is strictly positive if and only if
is a connected graph
. Intuitively, if the Cheeger constant is small but positive, then there exists a "bottleneck", in the sense that there are two "large" sets of vertices with "few" links (edges) between them. The Cheeger constant is "large" if any possible division of the vertex set into two subsets has "many" links between those two subsets.
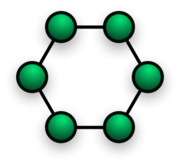In applications to theoretical computer science, one wishes to devise network configurations for which the Cheeger constant is high (at least, bounded away from zero) even when |V(G)| (the number of computers in the network) is large.
For example, consider a ring network
of N ≥ 3 computers, thought of as a graph GN. Number the computers 1, 2, ..., N clockwise around the ring. Mathematically, the vertex set is
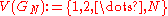
and the edge set is
Take A to be a collection of
of these computers in a connected chain:
Clearly,
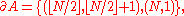
so
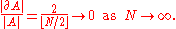
This example provides an upper bound for the Cheeger constant h(GN), which also tends to zero as N tends to infinity. Consequently, we would regard a ring network as highly "bottlenecked" for large N, and this is highly undesirable in practical terms. We would only need one of the computers on the ring to fail, and network performance would be greatly reduced. If two non-adjacent computers were to fail, the network would split into two disconnected components.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Cheeger constant (also Cheeger number or isoperimetric number) of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is a numerical measure of whether or not a graph has a "bottleneck". The Cheeger constant as a measure of "bottleneckedness" is of great interest in many areas: for example, constructing well-connected networks of computers, card shuffling, and low-dimensional topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
(in particular, the study of hyperbolic
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
3-manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s).
The Cheeger constant is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Jeff Cheeger
Jeff Cheeger
Jeff Cheeger , is a mathematician. Cheeger is professor at the Courant Institute of Mathematical Sciences at New York University in New York City. His main interests are differential geometry and its applications to topology and analysis.-Biography:He graduated from Harvard University with a B.A....
.
Definition
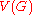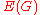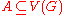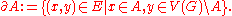
Let be an undirected graph with vertex set and edge set . For a collection of vertices , let denote the collection of all edges going from a vertex in to a vertex outside of :(Remember that edges are unordered, so the edge
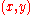is the same as the edge 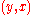.) Then the Cheeger constant of , denoted 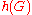, is defined by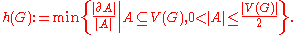The Cheeger constant is strictly positive if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
is a connected graphConnectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
. Intuitively, if the Cheeger constant is small but positive, then there exists a "bottleneck", in the sense that there are two "large" sets of vertices with "few" links (edges) between them. The Cheeger constant is "large" if any possible division of the vertex set into two subsets has "many" links between those two subsets.
Example: computer networking
For example, consider a ring network
Ring network
A ring network is a network topology in which each node connects to exactly two other nodes, forming a single continuous pathway for signals through each node - a ring...
of N ≥ 3 computers, thought of as a graph GN. Number the computers 1, 2, ..., N clockwise around the ring. Mathematically, the vertex set is
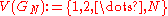
and the edge set is
Take A to be a collection of
of these computers in a connected chain:Clearly,
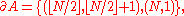
so
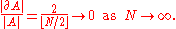
This example provides an upper bound for the Cheeger constant h(GN), which also tends to zero as N tends to infinity. Consequently, we would regard a ring network as highly "bottlenecked" for large N, and this is highly undesirable in practical terms. We would only need one of the computers on the ring to fail, and network performance would be greatly reduced. If two non-adjacent computers were to fail, the network would split into two disconnected components.
Cheeger Inequalities
The Cheeger constant is especially important in the context of expander graphs as it is a way to measure the edge expansion of a graph. The so-called Cheeger inequalities relate the Eigenvalue gap of a graph with its Cheeger constant.See also
- Algebraic connectivityAlgebraic connectivityThe algebraic connectivity of a graph G is the second-smallest eigenvalue of the Laplacian matrix of G. This eigenvalue is greater than 0 if and only if G is a connected graph. This is a corollary to the fact that the number of times 0 appears as an eigenvalue in the Laplacian is the number of...
- Cheeger boundCheeger boundIn mathematics, the Cheeger bound is a bound of the second largest eigenvalue of the transition matrix of a finite-state, discrete-time, reversible stationary Markov chain. It can be seen as a special case of Cheeger inequalities in expander graphs....
- Connectivity (graph theory)Connectivity (graph theory)In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
- Expander graphExpander graphIn combinatorics, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion as described below...