The Ars Magna is an important book on Algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

 written by Gerolamo Cardano

Gerolamo Cardano

Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...

. It was first published in 1545 under the title Artis Magnæ, Sive de Regulis Algebraicis Liber Unus (Book number one about The Great Art, or The Rules of Algebra). There was a second edition in Cardano's lifetime, published in 1570. It is considered one of the three greatest scientific treatises of the early Renaissance

Renaissance

The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...

, together with Copernicus' De revolutionibus orbium coelestium

De revolutionibus orbium coelestium

De revolutionibus orbium coelestium is the seminal work on the heliocentric theory of the Renaissance astronomer Nicolaus Copernicus...

and Vesalius

Vesalius

Andreas Vesalius was a Flemish anatomist, physician, and author of one of the most influential books on human anatomy, De humani corporis fabrica . Vesalius is often referred to as the founder of modern human anatomy. Vesalius is the Latinized form of Andries van Wesel...

' De humani corporis fabrica

De humani corporis fabrica

De humani corporis fabrica libri septem is a textbook of human anatomy written by Andreas Vesalius in 1543....

. The first editions of these three books were published within a two year span (1543–1545).

History

In 1535, Niccolò Fontana Tartaglia

Niccolò Fontana Tartaglia

Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...

 became famous for having solved cubics of the form x³ + ax = b (with a,b > 0). However, he chose to keep his method secret. In 1539, Cardano, then a lecturer in mathematics at the Piatti Foundation in Milan, published his first mathematical book, Pratica Arithmeticæ et mensurandi singularis (The Practice of Arithmetic and Simple Mensuration). That same year, he asked Tartaglia to explain to him his method for solving cubic equations. After some reluctance, Tartaglia did so, but he asked Cardano not to share the information until he published it. Cardano submerged himself in mathematics during the next several years working on how to extend Tartaglia's formula to other types of cubics. Furthermore, his student Lodovico Ferrari

Lodovico Ferrari

Lodovico Ferrari was an Italian mathematician.Born in Milan, Italy, grandfather, Bartholomew Ferrari was forced out of Milan to Bologna. He settled in Bologna, Italy and he began his career as the servant of Gerolamo Cardano. He was extremely bright, so Cardano started teaching him mathematics...

 found a way of solving quartic equations, but Ferrari's method depended upon Tartaglia's, since it involved the use of an auxiliary cubic equation. Then Cardano become aware of the fact that Scipione del Ferro

Scipione del Ferro

Scipione del Ferro was an Italian mathematician who first discovered a method to solve the depressed cubic equation.-Life:Scipione del Ferro was born in Bologna, in northern Italy, to Floriano and Filippa Ferro...

 had discovered Tartaglia's formula before Tartaglia himself, a discovery that prompted him to publish these results.

Contents

The book, which is divided into forty chapters, contains the first published solution to cubic and quartic equations. Cardano acknowledges that Tartaglia gave him the formula for solving a type of cubic equations and that the same formula had been discovered by Scipiano del Ferro. He also acknowledges that it was Ferrari who found a way of solving quartic equations.

Since at the time negative numbers were not generally acknowledged, knowing how to solve cubics of the form x³ + ax = b did not mean knowing how to solve cubics of the form x³ = ax + b (with a,b > 0), for instance. Besides, Cardano, also explains how to reduce equations of the form x³ + ax² + bx + c = 0 to cubic equations without a quadratic term, but, again, he has to consider several cases. In all, Cardano was driven to the study of thirteen different types of cubic equations (chapters XI–XXIII).

In Ars Magna the concept of multiple root appears for the first time (chapter I). The first example that Cardano provides of a polynomial equation with multiple roots is x³ = 12x + 16, of which −2 is a double root.

Ars Magna also contains the first occurrence of complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s (chapter XXXVII). Since (in modern notation) Cardano's formula for a root of the polynomial x³ + px + q  is
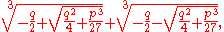
square roots of negative numbers appear naturally in this context. However, q²/4 + p³/27 never happens to be negative in the specific cases in which Cardano applies the formula. The problem mentioned by Cardano which leads to square roots of negative numbers is: find two numbers whose sum is equal to 10 and whose product is equal to 40. The answer is 5 + √−15 and 5 − √−15. Cardano called this "sophistic," because he saw no physical meaning to it, but boldly wrote "nevertheless we will operate" and formally calculated that their product does indeed equal 40. Cardano then says that this answer is “as subtle as it is useless”.

External links

• .pdf of Ars Magna (in Latin
  Latin
  Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
  
  )
• Cardano's biography