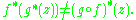Fibred category
Encyclopedia
Fibred categories are abstract entities in mathematics
used to provide a general framework for descent theory. They formalise the various situations in geometry
and algebra
in which inverse images (or pull-backs) of objects such as vector bundle
s can be defined. As an example, for each topological space there is the category of vector bundles on the space, and for every continuous map from a topological space X to another topological space Y is associated the pullback
functor
taking bundles on Y to bundles on X. Fibred categories formalise the system consisting of these categories and inverse image functors. Similar set-ups appear in various guises in mathematics, in particular in algebraic geometry
, which is the context in which fibred categories originally appeared. Fibrations also play an important role in categorical type theory
and theoretical computer science, particularly in models of dependent type
theory.
Fibred categories were introduced by Alexander Grothendieck
in Grothendieck (1959), and developed in more detail by himself and Jean Giraud
in Grothendieck (1971) in 1960/61, Giraud (1964) and Giraud (1971).
and geometry
where some types of objects are considered to exist on or above or over some underlying base space. The classical examples include vector bundles, principal bundle
s and sheaves
over topological spaces. Another example is given by "families" of algebraic varieties parametrised by another variety. Typical to these situations is that to a suitable type of a map
f: X → Y between base spaces, there is a corresponding inverse image (also called pull-back) operation f* taking the considered objects defined on Y to the same type of objects on X. This is indeed the case in the examples above: for example, the inverse image of a vector bundle E on Y is a vector bundle f*(E) on X.
Moreover, it is often the case that the considered "objects on a base space" form a category, or in other words have maps (morphisms) between them. In such cases the inverse image operation is often compatible with composition of these maps between objects, or in more technical terms is a functor
. Again, this is the case in examples listed above.
However, it is often the case that if g: Y → Z is another map, the inverse image functors are not strictly compatible with composed maps: if z is an object over Z (a vector bundle, say), it may well be that
Instead, these inverse images are only naturally
isomorphic
. This introduction of some "slack" in the system of inverse images causes some delicate issues to appear, and it is this set-up that fibred categories formalise.
The main application of fibred categories is in descent theory, concerned with a vast generalisation of "glueing" techniques used in topology. In order to support descent theory of sufficient generality to be applied in non-trivial situations in algebraic geometry the definition of fibred categories is quite general and abstract. However, the underlying intuition is quite straightforward when keeping in mind the basic examples discussed above.
issues related to "large" categories. The discussion can be made completely rigorous by, for example, restricting attention to small categories or by using universe
s.
between two categories
and S is an object of E, then the subcategory
of F consisting of those objects x for which φ(x)=S and those morphisms m satisfying φ(m)=idS, is called the fibre category (or fibre) over S, and is denoted FS. The morphisms of FS are called S-morphisms, and for x,y objects of FS, the set of S-morphisms is denoted by HomS(x,y). The image by φ of an object or a morphism in F is called its projection (by φ). If f is a morphism of E, then those morphisms of F that project to f are called f-morphisms, and the set of f-morphisms between objects x and y in F is denoted by Homf(x,y). A functor φ: F → E is also called an E-category, or said to make F into an E-category or a category over E. An E-functor from an E-category φ: F → E to an E-category ψ: G → E is a functor α: F → G such that ψ o α = φ. E-categories form in a natural manner a 2-category
, with 1-morphisms being E-functors, and 2-morphisms being natural transformations between E-functors whose components lie in some fibre.
A morphism m: x → y in F is called E-cartesian (or simply cartesian) if it satisfies the following condition:
A cartesian morphism m: x → y is called an inverse image of its projection f = φ(m); the object x is called an inverse image of y by f.
The cartesian morphisms of a fibre category FS are precisely the isomorphisms of FS. There can in general be more than one cartesian morphism projecting to a given morphism f: T → S, possibly having different sources; thus there can be more than one inverse image of a given object y in FS by f. However, it is a direct consequence of the definition that two such inverse images are isomorphic in FT.
An E-functor between two E-categories is called a cartesian functor if it takes cartesian morphisms to cartesian morphisms. Cartesian functors between two E-categories F,G form a category CartE(F,G), with natural transformations as morphisms. A special case is provided by considering E as an E-category via the identity functor: then a cartesian functor from E to an E-category F is called a cartesian section. Thus a cartesian section consists of a choice of one object xS in FS for each object S in E, and for each morphism f: T → S a choice of an inverse image mf: xT → xS. A cartesian section is thus a (strictly) compatible system of inverse images over objects of E. The category of cartesian sections of F is denoted by
In the important case where E has a terminal object
e (thus in particular when E is a topos
or the category E/S of arrows with target S in E) the functor
is fully faithful
(Lemma 5.7 of Giraud (1964)).
An E category φ: F → E is a fibred category (or a fibred E-category, or a category fibred over E) if each morphism f of E whose codomain is in the range of projection has at least one inverse image, and moreover the composition m o n of any two cartesian morphisms m,n in F is always cartesian. In other words, an E-category is a fibred category if inverse images always exist (for morphisms whose codomains are in the range of projection) and are transitive.
If E has a terminal object e and if F is fibred over E, then the functor ε from cartesian sections to Fe defined at the end of the previous section is an equivalence of categories
and moreover surjective on objects.
If F is a fibred E-category, it is always possible, for each morphism f: T → S in E and each object y in FS, to choose (by using the axiom of choice) precisely one inverse image m: x → y. The class of morphisms thus selected is called a cleavage and the selected morphisms are called the transport morphisms (of the cleavage). A fibred category together with a cleavage is called a cleaved category. A cleavage is called normalised if the transport morphisms include all identities in F; this means that the inverse images of identity morphisms are chosen to be identity morphisms. Evidently if a cleavage exists, it can be chosen to be normalised; we shall consider only normalised cleavages below.
The choice of a (normalised) cleavage for a fibred E-category F specifies, for each morphism f: T → S in E, a functor f*: FS → FT: on objects f* is simply the inverse image by the corresponding transport morphism, and on morphisms it is defined in a natural manner by the defining universal property of cartesian morphisms. The operation which associates to an object S of E the fibre category FS and to a morphism f the inverse image functor f* is almost a contravariant functor from E to the category of categories. However, in general it fails to commute strictly with composition of morphisms. Instead, if f: T → S and g: U → T are morphisms in E, then there is an isomorphism of functors
These isomorphisms satisfy the following two compatibilities:
It can be shown (see Grothendieck (1971) section 8) that, inversely, any collection of functors f*: FS → FT together with isomorphisms cf,g satisfying the compatibilities above, defines a cleaved category. These collections of inverse image functors provide a more intuitive view on fibred categories; and indeed, it was in terms of such compatible inverse image functors that fibred categories were introduced in Grothendieck (1959).
The paper by Gray referred to below makes analogies between these ideas and the notion of fibration
of spaces.
These ideas simplify in the case of groupoids, as shown in the paper of Brown referred to below, which obtains a useful family of exact sequences from a fibration of groupoids.
Unlike cleavages, not all fibred categories admit splittings. For an example, see below.
Similarly the split categories over E form a 2-category Scin(E) (from French catégorie scindée), where the category of morphisms between two split categories F and G is the full sub-category ScinE(F,G) of E-functors from F to G consisting of those functors that transform each transport morphism of F into a transport morphism of G. Each such morphism of split E-categories is also a morphism of E-fibred categories, i.e., ScinE(F,G) ⊂ CartE(F,G).
There is a natural forgetful 2-functor i: Scin(E) → Fib(E) that simply forgets the splitting.
associated to a fibred category (and in particular stack associated to a pre-stack).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
used to provide a general framework for descent theory. They formalise the various situations in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
in which inverse images (or pull-backs) of objects such as vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s can be defined. As an example, for each topological space there is the category of vector bundles on the space, and for every continuous map from a topological space X to another topological space Y is associated the pullback
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
taking bundles on Y to bundles on X. Fibred categories formalise the system consisting of these categories and inverse image functors. Similar set-ups appear in various guises in mathematics, in particular in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, which is the context in which fibred categories originally appeared. Fibrations also play an important role in categorical type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
and theoretical computer science, particularly in models of dependent type
Dependent type
In computer science and logic, a dependent type is a type that depends on a value. Dependent types play a central role in intuitionistic type theory and in the design of functional programming languages like ATS, Agda and Epigram....
theory.
Fibred categories were introduced by Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
in Grothendieck (1959), and developed in more detail by himself and Jean Giraud
Jean Giraud (mathematician)
Jean Giraud was a French mathematician, a student of Alexander Grothendieck and the author of the book "Cohomologie non abélienne" ....
in Grothendieck (1971) in 1960/61, Giraud (1964) and Giraud (1971).
Background and motivations
There are many examples in topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
where some types of objects are considered to exist on or above or over some underlying base space. The classical examples include vector bundles, principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s and sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
over topological spaces. Another example is given by "families" of algebraic varieties parametrised by another variety. Typical to these situations is that to a suitable type of a map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
f: X → Y between base spaces, there is a corresponding inverse image (also called pull-back) operation f* taking the considered objects defined on Y to the same type of objects on X. This is indeed the case in the examples above: for example, the inverse image of a vector bundle E on Y is a vector bundle f*(E) on X.
Moreover, it is often the case that the considered "objects on a base space" form a category, or in other words have maps (morphisms) between them. In such cases the inverse image operation is often compatible with composition of these maps between objects, or in more technical terms is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
. Again, this is the case in examples listed above.
However, it is often the case that if g: Y → Z is another map, the inverse image functors are not strictly compatible with composed maps: if z is an object over Z (a vector bundle, say), it may well be that
Instead, these inverse images are only naturally
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. This introduction of some "slack" in the system of inverse images causes some delicate issues to appear, and it is this set-up that fibred categories formalise.
The main application of fibred categories is in descent theory, concerned with a vast generalisation of "glueing" techniques used in topology. In order to support descent theory of sufficient generality to be applied in non-trivial situations in algebraic geometry the definition of fibred categories is quite general and abstract. However, the underlying intuition is quite straightforward when keeping in mind the basic examples discussed above.
Formal definitions
There are two essentially equivalent technical definitions of fibred categories, both of which will be described below. All discussion in this section ignores the set-theoreticalSet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
issues related to "large" categories. The discussion can be made completely rigorous by, for example, restricting attention to small categories or by using universe
Grothendieck universe
In mathematics, a Grothendieck universe is a set U with the following properties:# If x is an element of U and if y is an element of x, then y is also an element of U...
s.
Cartesian morphisms and functors
If φ: F → E is a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
between two categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and S is an object of E, then the subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of F consisting of those objects x for which φ(x)=S and those morphisms m satisfying φ(m)=idS, is called the fibre category (or fibre) over S, and is denoted FS. The morphisms of FS are called S-morphisms, and for x,y objects of FS, the set of S-morphisms is denoted by HomS(x,y). The image by φ of an object or a morphism in F is called its projection (by φ). If f is a morphism of E, then those morphisms of F that project to f are called f-morphisms, and the set of f-morphisms between objects x and y in F is denoted by Homf(x,y). A functor φ: F → E is also called an E-category, or said to make F into an E-category or a category over E. An E-functor from an E-category φ: F → E to an E-category ψ: G → E is a functor α: F → G such that ψ o α = φ. E-categories form in a natural manner a 2-category
2-category
In category theory, a 2-category is a category with "morphisms between morphisms"; that is, where each hom set itself carries the structure of a category...
, with 1-morphisms being E-functors, and 2-morphisms being natural transformations between E-functors whose components lie in some fibre.
A morphism m: x → y in F is called E-cartesian (or simply cartesian) if it satisfies the following condition:
- if f: T → S is the projection of m, and if n: z → y is an f-morphism, then there is precisely one T-morphism a: z → x such that n = m o a.
A cartesian morphism m: x → y is called an inverse image of its projection f = φ(m); the object x is called an inverse image of y by f.
The cartesian morphisms of a fibre category FS are precisely the isomorphisms of FS. There can in general be more than one cartesian morphism projecting to a given morphism f: T → S, possibly having different sources; thus there can be more than one inverse image of a given object y in FS by f. However, it is a direct consequence of the definition that two such inverse images are isomorphic in FT.
An E-functor between two E-categories is called a cartesian functor if it takes cartesian morphisms to cartesian morphisms. Cartesian functors between two E-categories F,G form a category CartE(F,G), with natural transformations as morphisms. A special case is provided by considering E as an E-category via the identity functor: then a cartesian functor from E to an E-category F is called a cartesian section. Thus a cartesian section consists of a choice of one object xS in FS for each object S in E, and for each morphism f: T → S a choice of an inverse image mf: xT → xS. A cartesian section is thus a (strictly) compatible system of inverse images over objects of E. The category of cartesian sections of F is denoted by
In the important case where E has a terminal object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
e (thus in particular when E is a topos
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
or the category E/S of arrows with target S in E) the functor
is fully faithful
Full and faithful functors
In category theory, a faithful functor is a functor which is injective when restricted to each set of morphisms that have a given source and target....
(Lemma 5.7 of Giraud (1964)).
Fibred categories and cleaved categories
The technically most flexible and economical definition of fibred categories is based on the concept of cartesian morphisms. It is equivalent to a definition in terms of cleavages, the latter definition being actually the original one presented in Grothendieck (1959); the definition in terms of cartesian morphisms was introduced in Grothendieck (1974) in 1960–1961.An E category φ: F → E is a fibred category (or a fibred E-category, or a category fibred over E) if each morphism f of E whose codomain is in the range of projection has at least one inverse image, and moreover the composition m o n of any two cartesian morphisms m,n in F is always cartesian. In other words, an E-category is a fibred category if inverse images always exist (for morphisms whose codomains are in the range of projection) and are transitive.
If E has a terminal object e and if F is fibred over E, then the functor ε from cartesian sections to Fe defined at the end of the previous section is an equivalence of categories
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
and moreover surjective on objects.
If F is a fibred E-category, it is always possible, for each morphism f: T → S in E and each object y in FS, to choose (by using the axiom of choice) precisely one inverse image m: x → y. The class of morphisms thus selected is called a cleavage and the selected morphisms are called the transport morphisms (of the cleavage). A fibred category together with a cleavage is called a cleaved category. A cleavage is called normalised if the transport morphisms include all identities in F; this means that the inverse images of identity morphisms are chosen to be identity morphisms. Evidently if a cleavage exists, it can be chosen to be normalised; we shall consider only normalised cleavages below.
The choice of a (normalised) cleavage for a fibred E-category F specifies, for each morphism f: T → S in E, a functor f*: FS → FT: on objects f* is simply the inverse image by the corresponding transport morphism, and on morphisms it is defined in a natural manner by the defining universal property of cartesian morphisms. The operation which associates to an object S of E the fibre category FS and to a morphism f the inverse image functor f* is almost a contravariant functor from E to the category of categories. However, in general it fails to commute strictly with composition of morphisms. Instead, if f: T → S and g: U → T are morphisms in E, then there is an isomorphism of functors
These isomorphisms satisfy the following two compatibilities:
-
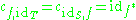
- for three consecutive morphisms
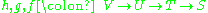and object 
the following holds: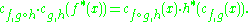 
It can be shown (see Grothendieck (1971) section 8) that, inversely, any collection of functors f*: FS → FT together with isomorphisms cf,g satisfying the compatibilities above, defines a cleaved category. These collections of inverse image functors provide a more intuitive view on fibred categories; and indeed, it was in terms of such compatible inverse image functors that fibred categories were introduced in Grothendieck (1959).
The paper by Gray referred to below makes analogies between these ideas and the notion of fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
of spaces.
These ideas simplify in the case of groupoids, as shown in the paper of Brown referred to below, which obtains a useful family of exact sequences from a fibration of groupoids.
Splittings and split fibred categories
A (normalised) cleavage such that the composition of two transport morphisms is always a transport morphisms is called a splitting, and a fibred category with a splitting is called a split (fibred) category. In terms of inverse image functors the condition of being a splitting means that the composition of inverse image functors corresponding to composable morphisms f,g in E equals the inverse image functor corresponding to f o g. In other words, the compatibility isomorphisms cf,g of the previous section are all identities for a split category. Thus split E-categories correspond exactly to true functors from E to the category of categories.Unlike cleavages, not all fibred categories admit splittings. For an example, see below.
Co-cartesian morphisms and co-fibred categories
One can invert the direction of arrows in the definitions above to arrive at corresponding concepts of co-cartesian morphisms, co-fibred categories and split co-fibred categories (or co-split categories). More precisely, if φ: F →E is a functor, then a morphism m: x → y in F is called co-cartesian if it is cartesian for the opposite functor φop: Fop → Eop. Then m is also called a direct image and y a direct image of x for f = φ(m). A co-fibred E-category is anE-category such that direct image exists for each morphism in E and that the composition of direct images is a direct image. A co-cleavage and a co-splitting are defined similarly, corresponding to direct image functors instead of inverse image functors.The 2-categories of fibred categories and split categories
The categories fibred over a fixed category E form a 2-category Fib(E), where the category of morphisms between two fibred categories F and G is defined to be the category CartE(F,G) of cartesian functors from F to G.Similarly the split categories over E form a 2-category Scin(E) (from French catégorie scindée), where the category of morphisms between two split categories F and G is the full sub-category ScinE(F,G) of E-functors from F to G consisting of those functors that transform each transport morphism of F into a transport morphism of G. Each such morphism of split E-categories is also a morphism of E-fibred categories, i.e., ScinE(F,G) ⊂ CartE(F,G).
There is a natural forgetful 2-functor i: Scin(E) → Fib(E) that simply forgets the splitting.
Existence of equivalent split categories
While not all fibred categories admit a splitting, each fibred category is in fact equivalent to a split category. Indeed, there are two canonical ways to construct an equivalent split category for a given fibred category F over E. More precisely, the forgetful 2-functor i: Scin(E) → Fib(E) admits a right 2-adjoint S and a left 2-adjoint L (Theorems 2.4.2 and 2.4.4 of Giraud 1971), and S(F) and L(F) are the two associated split categories. The adjunction functors S(F) → F and F → L(F) are both cartesian and equivalences (ibid.). However, while their composition S(F) → L(F) is an equivalence (of categories, and indeed of fibred categories), it is not in general a morphism of split categories. Thus the two constructions differ in general. The two preceding constructions of split categories are used in a critical way in the construction of the stackStack (descent theory)
In mathematics a stack is a concept used to formalise some of the main constructions of descent theory.Descent theory is concerned with generalisations of situations where geometrical objects can be "glued together" when they are isomorphic when restricted to intersections of the sets in an open...
associated to a fibred category (and in particular stack associated to a pre-stack).
Examples
- Categories of arrows: For any category E the category of arrows A(E) in E has as objects the morphisms in E, and as morphisms the commutative squares in E (more precisely, a morphism from (f: X → T) to (g: Y → S) consists of morphisms (a: X → Y) and (b: T → S) such that bf = ga). The functor which takes an arrow to its target makes A(E) into an E-category; for an object S of E the fibre ES is the category E/S of S-objects in E, i.e., arrows in E with target S. Cartesian morphisms in A(E) are precisely the cartesian squares in E, and thus A(E) is fibred over E precisely when fibre products exist in E.
- Fibre bundles: Fibre products exist in the category Top of topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and thus by the previous example A(Top) is fibred over Top. If Fib is the full subcategory of A(Top) consisting of arrows that are projection maps of fibre bundles, then FibS is the category of fibre bundles on S and Fib is fibred over Top. A a choice of a cleavage amounts to a choice of ordinary inverse image (or pull-back) functors for fibre bundles. - Vector bundles: In a manner similar to the previous examples the projections (p: V → S) of real (complex) vector bundles to their base spaces form a category VectR (VectC) over Top (morphisms of vector bundles respecting the vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
structure of the fibres). This Top-category is also fibred, and the inverse image functors (are the ordinary pull-back functors for vector bundles. These fibred categories are (non-full) subcategories of Fib. - Sheaves on topological spaces: The inverse image functors of sheavesSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
make the categories Sh(S) of sheaves on topological spaces S into a (cleaved) fibred category Sh over Top. This fibred category can be described as the full sub-category of A(Top) consisting of etale spaces of sheaves. As with vector bundles, the sheaves of groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and ringsRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
also form fibred categories of Top. - Sheaves on topoi: If E is a toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
and S is an object in E, the category ES of S-objects is also a topos, interpreted as the category of sheaves on S. If f: T → S is a morphism in E, the inverse image functor f* can be described as follows: for a sheaf F on ES and an object p: U → T in ET one has f*F(U) = HomT(U, f*F) equals HomS(f o p, F) = F(U). These inverse image make the categories ES into a split fibred category on E. This can be applied in particular to the "large" topos TOP of topological spaces. - Quasi-coherent sheaves on schemes: Quasi-coherent sheaves form a fibred category over the category of schemesScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. This is one of the motivating examples for the definition of fibred categories. - Fibred category admitting no splitting: A group G can be considered as a category with one object and the elements of G as the morphisms, composition of morphisms being given by the group law. A group homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
f: G → H can then be considered as a functor, which makes G into a H-category. It can be checked that in this set-up all morphisms in G are cartesian; hence G is fibred over H precisely when f is surjective. A splitting in this setup is a (set-theoretic) sectionSection (category theory)In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of f which commutes strictly with composition, or in other words a section of f which is also a homomorphism. But as is well-known in group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, this is not always possible (one can take the projection in a non-split group extensionGroup extensionIn mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
). - Co-fibred category of sheaves: The direct image functor of sheaves makes the categories of sheaves on topological spaces into a co-fibred category. The transitivity of the direct image shows that this is even naturally co-split.