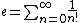Proof that e is irrational
Encyclopedia
In mathematics
, the series representation
of Euler's number e
can be used to prove that e is irrational
. Of the many representations of e
, this is the Taylor series
for the exponential function
evaluated at y = 1.
's proof by contradiction
. Initially e is assumed to be a rational number of the form a/b. We then analyze a blown-up difference x of the series representing e and its strictly smaller partial sum, which approximates the limiting value e. By choosing the magnifying factor to be the factorial
of b, the fraction a/b and the partial sum are turned into integers, hence x must be a positive integer. However, the fast convergence of the series representation implies that the magnified approximation error x is still strictly smaller than 1. From this contradiction we deduce that e is irrational.
. Then there exist positive integers a and b such that e = a/b.
Define the number
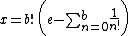
To see that if e is rational, then x is an integer, substitute e = a/b into this definition to obtain
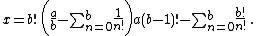
The first term is an integer, and every fraction in the sum is actually an integer because n ≤ b for each term. Therefore x is an integer.
We now prove that . First, to prove that x is strictly positive, we insert the above series representation of e into the definition of x and obtain
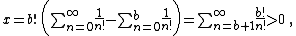
because all the terms with n ≤ b cancel and the remaining ones are strictly positive.
We now prove that x < 1. For all terms with we have the upper estimate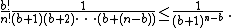
This inequality is strict for every n ≥ b + 2. Changing the index of summation to k = n – b and using the formula for the infinite geometric series, we obtain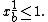
Since there is no integer strictly between 0 and 1, we have reached a contradiction, and so e must be irrational. Q.E.D.
The above proof can be found in Proofs from THE BOOK
, where the stronger result that eq is irrational for any non-zero rational q is also proved.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the series representation
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of Euler's number e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
can be used to prove that e is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. Of the many representations of e
Representations of e
The mathematical constant e can be represented in a variety of ways as a real number. Since e is an irrational number , it cannot be represented as a fraction, but it can be represented as a continued fraction...
, this is the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
evaluated at y = 1.
Summary of the proof
This is Joseph FourierJoseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
's proof by contradiction
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
. Initially e is assumed to be a rational number of the form a/b. We then analyze a blown-up difference x of the series representing e and its strictly smaller partial sum, which approximates the limiting value e. By choosing the magnifying factor to be the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of b, the fraction a/b and the partial sum are turned into integers, hence x must be a positive integer. However, the fast convergence of the series representation implies that the magnified approximation error x is still strictly smaller than 1. From this contradiction we deduce that e is irrational.
Proof
Towards a contradiction, suppose that e is a rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. Then there exist positive integers a and b such that e = a/b.
Define the number
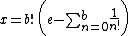
To see that if e is rational, then x is an integer, substitute e = a/b into this definition to obtain
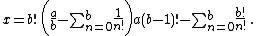
The first term is an integer, and every fraction in the sum is actually an integer because n ≤ b for each term. Therefore x is an integer.
We now prove that . First, to prove that x is strictly positive, we insert the above series representation of e into the definition of x and obtain
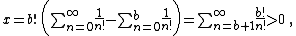
because all the terms with n ≤ b cancel and the remaining ones are strictly positive.
We now prove that x < 1. For all terms with we have the upper estimate
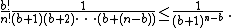
This inequality is strict for every n ≥ b + 2. Changing the index of summation to k = n – b and using the formula for the infinite geometric series, we obtain
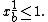
Since there is no integer strictly between 0 and 1, we have reached a contradiction, and so e must be irrational. Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
The above proof can be found in Proofs from THE BOOK
Proofs from THE BOOK
Proofs from THE BOOK is a book of mathematical proofs by Martin Aigner and Günter M. Ziegler. The book is dedicated to the mathematician Paul Erdős, who often referred to "The Book" in which God keeps the most elegant proof of each mathematical theorem...
, where the stronger result that eq is irrational for any non-zero rational q is also proved.
See also
- Characterizations of the exponential functionCharacterizations of the exponential functionIn mathematics, the exponential function can be characterized in many ways. The following characterizations are most common. This article discusses why each characterization makes sense, and why the characterizations are independent of and equivalent to each other...
- Transcendental numberTranscendental numberIn mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
, including a proof that e is transcendental - Lindemann–Weierstrass theoremLindemann–Weierstrass theoremIn mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...