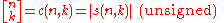In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, Stirling numbers arise in a variety of combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

 problems. They are named after James Stirling

James Stirling (mathematician)

James Stirling was a Scottish mathematician. The Stirling numbers and Stirling's approximation are named after him.-Biography:...

, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind

Stirling numbers of the first kind

In mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be...

 and the Stirling numbers of the second kind.

Notation

Several different notations for the Stirling numbers are in use. Stirling numbers of the first kind are written with a small s, and those of the second kind with a large S (Abramowitz and Stegun

Abramowitz and Stegun

Abramowitz and Stegun is the informal name of a mathematical reference work edited by Milton Abramowitz and Irene Stegun of the U.S. National Bureau of Standards...

 use an uppercase S and a blackletter

Blackletter

Blackletter, also known as Gothic script, Gothic minuscule, or Textura, was a script used throughout Western Europe from approximately 1150 to well into the 17th century. It continued to be used for the German language until the 20th century. Fraktur is a notable script of this type, and sometimes...

 S respectively). Common notations are:

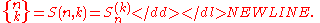
The notation of using brackets and braces, in analogy to the binomial coefficients, was introduced in 1935 by Jovan Karamata

Jovan Karamata

Jovan Karamata was one of the greatest Serbian mathematicians of the 20th century. He is remembered for contributions to analysis, in particular, the Tauberian theory and the theory of slowly varying functions...

 and promoted later by Donald Knuth

Donald Knuth

Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...

; it is referred to as Karamata notation. (The bracket notation conflicts with a common notation for the Gaussian coefficients.) The mathematical motivation for this type of notation, as well as additional Stirling number formulae, may be found on the page for Stirling numbers and exponential generating functions

Stirling numbers and exponential generating functions

The use of exponential generating functions to study the properties of Stirling numbers is a classical exercise in combinatorics and possibly the canonical example of how symbolic combinatorics, the method that encapsulates the fundamental theorem of combinatorial enumeration, is used...

.

Stirling numbers of the first kind

Unsigned Stirling numbers of the first kind


(with a lower-case "s") count the number of permutation

Permutation

In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...

s of n elements with k disjoint cycle

Cyclic permutation

A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...

s.

Stirling numbers of the first kind (without the qualifying adjective unsigned) are the coefficients in the expansion


where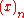 is the Pochhammer symbol

Pochhammer symbol

In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...

 for the falling factorial,


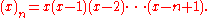
Note that (x)₀ = 1 because it is an empty product

Empty product

In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...

. Combinatorialists

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

 also sometimes use the notation $x^\{\backslash underline\{n\backslash !\}\}$ for the falling factorial, and $x^\{\backslash overline\{n\backslash !\}\}$ for the rising factorial.

(Confusingly, the Pochhammer symbol that many use for falling factorials is used in special functions for rising factorials.)

Stirling numbers of the second kind

Stirling numbers of the second kind count the number of ways to partition a set of n elements into k nonempty subsets. They are denoted by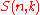 or . The sum


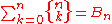
is the nth Bell number. Using falling factorials, we can also characterize the Stirling numbers of the second kind by


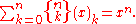
The Lah number, are sometimes being referred as Stirling numbers of the third kind. for example see.

Inversion relationships

The Stirling numbers of the first and second kind can be considered to be inverses of one another:


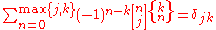
and


where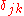 is the Kronecker delta. These two relationships may be understood to be matrix inverses. That is, let s be the lower triangular matrix of Stirling numbers of first kind, so that it has matrix elements


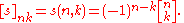
Then, the inverse of this matrix is S, the lower triangular matrix of Stirling numbers of second kind. Symbolically, one writes


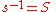
where the matrix elements of S are


Note that although s and S are infinite, this works for finite matrices by only considering Stirling numbers up to some number N.

A generalization of the inversion relationship gives the link with Lah numbers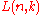


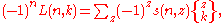
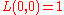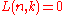with the conventions and if .

Symmetric formulae

Abramowitz and Stegun give the following symmetric formulae that relate the Stirling numbers of the first and second kind.


and

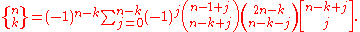
See also

• Bell polynomials
• Cycles and fixed points
• Lah number
  Lah number
  In mathematics, Lah numbers, discovered by Ivo Lah in 1955, are coefficients expressing rising factorials in terms of falling factorials.Unsigned Lah numbers have an interesting meaning in combinatorics: they count the number of ways a set of n elements can be partitioned into k nonempty linearly...
  
  
• Pochhammer symbol
  Pochhammer symbol
  In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
  
  
• Polynomial sequence
  Polynomial sequence
  In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
  
  
• Stirling transform
• Touchard polynomials

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.