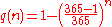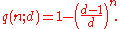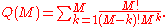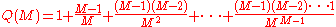Birthday paradox
Encyclopedia
In probability theory
, the birthday problem or birthday paradox
pertains to the probability
that, in a set of n randomly chosen people, some pair of them will have the same birthday
. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 366. However, 99% probability is reached with just 57 people, and 50% probability with 23 people. These conclusions are based on the assumption that each day of the year (except February 29) is equally probable for a birthday.
The mathematics behind this problem led to a well-known cryptographic attack called the birthday attack
, which uses this probabilistic model to reduce the complexity of cracking a hash function
.
In the example given earlier, a list of 23 people, comparing the birthday of the first person on the list to the others allows 22 chances for a matching birthday (The second person on the list to the others allows 21 chances for a matching birthday, third person has 20 chances, and so on. Hence 22+21+20+....+1 = 253), but comparing every person to all of the others allows 253 distinct chances (combination
s): in a group of 23 people there are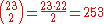 pairs.
pairs.
Presuming all birthdays are equally probable, the probability of a given birthday for a person chosen from the entire population at random is 1/365 (ignoring Leap Day, February 29). Although the pairings in a group of 23 people are not statistically equivalent to 253 pairs chosen independently, the birthday paradox becomes less surprising if a group is thought of in terms of the number of possible pairs, rather than as the number of individuals.
s, twin
s, seasonal or weekday variations, and assume that the 365 possible birthdays are equally likely. Real-life birthday distributions are not uniform since not all dates are equally likely.
If P(A) is the probability of at least two people in the room having the same birthday, it may be simpler to calculate P(A' ), the probability of there not being any two people having the same birthday. Then, because P(A) and P(A' ) are the only two possibilities and are also mutually exclusive, P(A' ) = 1 − P(A).
In deference to widely published solutions concluding that 23 is the number of people necessary to have a P(A) that is greater than 50%, the following calculation of P(A) will use 23 people as an example.
When events are independent of each other, the probability of all of the events occurring is equal to a product of the probabilities of each of the events occurring. Therefore, if P(A') can be described as 23 independent events, P(A' ) could be calculated as P(1) × P(2) × P(3) × ... × P(23).
The 23 independent events correspond to the 23 people, and can be defined in order. Each event can be defined as the corresponding person not sharing their birthday with any of the previously analyzed people. For Event 1, there are no previously analyzed people. Therefore, the probability, P(1), that person number 1 does not share his/her birthday with previously analyzed people is 1, or 100%. Ignoring leap years for this analysis, the probability of 1 can also be written as 365/365, for reasons that will become clear below.
For Event 2, the only previously analyzed people are Person 1. Assuming that birthdays are equally likely to happen on each of the 365 days of the year, the probability, P(2), that Person 2 has a different birthday than Person 1 is 364/365. This is because, if Person 2 was born on any of the other 364 days of the year, Persons 1 and 2 will not share the same birthday.
Similarly, if Person 3 is born on any of the 363 days of the year other than the birthdays of Persons 1 and 2, Person 3 will not share their birthday. This makes the probability P(3) = 363/365.
This analysis continues until Person 23 is reached, whose probability of not sharing their birthday with people analyzed before, P(23), is 343/365.
P(A' ) is equal to the product of these individual probabilities:
The terms of equation (1) can be collected to arrive at:
Evaluating equation (2) gives P(A' ) = 0.492703
Therefore, P(A) = 1 − 0.492703 = 0.507297 (50.7297%)
This process can be generalized to a group of n people, where p(n) is the probability of at least two of the n people sharing a birthday. It is easier to first calculate the probability p(n) that all n birthdays are different. According to the pigeonhole principle, p(n) is zero when n > 365. When n ≤ 365:
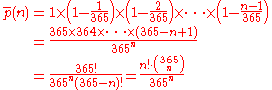
where ' ! ' is the factorial
operator.
The equation expresses the fact that for no persons to share a birthday, a second person cannot have the same birthday as the first (364/365), the third cannot have the same birthday as the first two (363/365), and in general the nth birthday cannot be the same as any of the n − 1 preceding birthdays.
The event
of at least two of the n persons having the same birthday is complementary
to all n birthdays being different. Therefore, its probability p(n) is
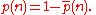
This probability surpasses 1/2 for n = 23 (with value about 50.7%). The following table shows the probability for some other values of n (this table ignores the existence of leap years, as described above):
expansion of the exponential function
(the constant e = 2.718281828, approximately)
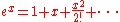
provides a first-order approximation for ex for x << 1:

The first expression derived for p(n) can be approximated as
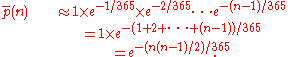
Therefore,
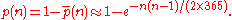
An even coarser approximation is given by
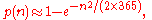
which, as the graph illustrates, is still fairly accurate.
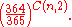
And if this is the probability of no one having the same birthday, then the probability of someone sharing a birthday is
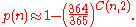
approximation for the binomial,
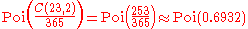
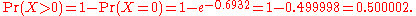
Again, this is over 50%.

This is a result of the good approximation that an event with 1 in k probability will have a 50% chance of occurring at least once if it is repeated k ln 2 times.
.
As stated above, the probability that no two birthdays coincide is
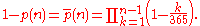
As in earlier paragraphs, interest lies in the smallest n such that p(n) > 1/2; or equivalently, the smallest n such that p(n) < 1/2.
Using the inequality 1 − x < e−x in the above expression we replace 1 − k/365 with e−k/365. This yields
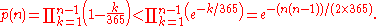
Therefore, the expression above is not only an approximation, but also an upper bound
of p(n). The inequality

implies p(n) < 1/2. Solving for n gives

Now, 730 ln 2 is approximately 505.997, which is barely below 506, the value of n2 − n attained when n = 23. Therefore, 23 people suffice.
Solving n2 − n = 2 · 365 · ln 2 for n gives, by the way, the approximate formula of Frank H. Mathis cited above.
This derivation only shows that at most 23 people are needed to ensure a birthday match with even chance; it leaves open the possibility that, say, n = 22 could also work.
The generic results can be derived using the same arguments given above.
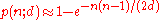

Conversely, if n(p;d) denotes the number of random integers drawn from [1,d] to obtain a probability p that at least two numbers are the same, then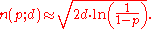
The birthday problem in this more generic sense applies to hash function
s: the expected number of N-bit
hashes that can be generated before getting a collision is not 2N, but rather only 2N/2. This is exploited by birthday attack
s on cryptographic hash function
s and is the reason why a small number of collisions in a hash table
are, for all practical purposes, inevitable.
The theory behind the birthday problem was used by Zoe Schnabel under the name of capture-recapture
statistics to estimate the size of fish population in lakes.
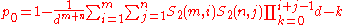
where d = 365 and S2 are Stirling numbers of the second kind
. Consequently, the desired probability is 1 − p0.
This variation of the birthday problem is interesting because there is not a unique solution for the total number of people m + n. For example, the usual 0.5 probability value is realized for both a 32-member group of 16 men and 16 women and a 49-member group of 43 women and 6 men.
Taking the above formula for d = 365 we have:
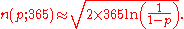
Note: some values falling outside the bounds have been colored to show that the approximation is not always exact.
and for general d by
In the standard case of d = 365 substituting n = 23 gives about 6.1%, which is less than 1 chance in 16. For a greater than 50% chance that one person in a roomful of n people has the same birthday as you, n would need to be at least 253. Note that this number is significantly higher than 365/2 = 182.5: the reason is that it is likely that there are some birthday matches among the other people in the room.
It is not a coincidence that ; a similar approximate pattern can be found using a number of possibilities different from 365, or a target probability different from 50%.
; a similar approximate pattern can be found using a number of possibilities different from 365, or a target probability different from 50%.
. The number of people required so that the probability that some pair will have a birthday separated by fewer than k days will be higher than 50% is:
Thus in a group of just seven random people, it is more likely than not that two of them will have a birthday within a week of each other.
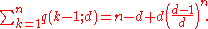
analyzed by Donald Knuth
in his book The Art of Computer Programming
. It may be shown that if one samples uniformly, with replacement, from a population of size M, the number of trials required for the first repeated sampling of some individual has expected value
 , where
, where
The function
has been studied by Srinivasa Ramanujan
and has asymptotic expansion
:
With M = 365 days in a year, the average number of people required to find a pair with the same birthday is , slightly more than the number required for a 50% chance. In the best case, two people will suffice; at worst, the maximum possible number of M + 1 = 366 people is needed; but on average
, slightly more than the number required for a 50% chance. In the best case, two people will suffice; at worst, the maximum possible number of M + 1 = 366 people is needed; but on average
, only 25 people are required.
An informal demonstration of the problem can be made from the list of Prime Ministers of Australia, in which Paul Keating
, the 24th Prime Minister, and Edmund Barton
, the first Prime Minister, share same birthday i.e. 18 January.
James K. Polk
and Warren G. Harding
, the 11th and 29th Presidents of the United States, were both born on November 2.
Sir John A. Macdonald
and Jean Chrétien
, the 1st and 20th Prime Ministers of Canada, were both born on January 11.
Of the 73 male actors to win the Academy Award for Best Actor
, there are six pairs of actors who share the same birthday.
Of the 67 actresses to win the Academy Award for Best Actress
, there are three pairs of actresses who share the same birthday.
Of the 61 directors to win the Academy Award for Best Director, there are five pairs of directors who share the same birthday.
Of the 52 people to serve as Prime Minister of the United Kingdom
, there are two pairs of men who share the same birthday.
, a variant of the knapsack problem
from operations research. Some weights are put on a balance scale
; each weight is an integer number of grams randomly chosen between one gram and one million grams (one metric ton). The question is whether one can usually (that is, with probability close to 1) transfer the weights between the left and right arms to balance the scale. (In case the sum of all the weights is an odd number of grams, a discrepancy of one gram is allowed.) If there are only two or three weights, the answer is very clearly no; although there are some combinations which work, the majority of randomly selected combinations of three weights do not. If there are very many weights, the answer is clearly yes. The question is, how many are just sufficient? That is, what is the number of weights such that it is equally likely for it to be possible to balance them as it is to be impossible?
Some people's intuition is that the answer is above 100,000. Most people's intuition is that it is in the thousands or tens of thousands, while others feel it should at least be in the hundreds. The correct answer is approximately 23.
The reason is that the correct comparison is to the number of partitions of the weights into left and right. There are 2N−1 different partitions for N weights, and the left sum minus the right sum can be thought of as a new random quantity for each partition. The distribution of the sum of weights is approximately Gaussian, with a peak at 1,000,000 N and width , so that when 2N−1 is approximately equal to
, so that when 2N−1 is approximately equal to  the transition occurs. 223−1 is about 4 million, while the width of the distribution is only 5 million.
the transition occurs. 223−1 is about 4 million, while the width of the distribution is only 5 million.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the birthday problem or birthday paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
pertains to the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that, in a set of n randomly chosen people, some pair of them will have the same birthday
Birthday
A birthday is a day or anniversary where a person celebrates his or her date of birth. Birthdays are celebrated in numerous cultures, often with a gift, party or rite of passage. Although the major religions celebrate the birth of their founders , Christmas – which is celebrated widely by...
. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 366. However, 99% probability is reached with just 57 people, and 50% probability with 23 people. These conclusions are based on the assumption that each day of the year (except February 29) is equally probable for a birthday.
The mathematics behind this problem led to a well-known cryptographic attack called the birthday attack
Birthday attack
A birthday attack is a type of cryptographic attack that exploits the mathematics behind the birthday problem in probability theory. This attack can be used to abuse communication between two or more parties...
, which uses this probabilistic model to reduce the complexity of cracking a hash function
Hash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
.
Understanding the problem
The birthday problem asks whether any of the people in a given group has a birthday matching any of the others — not one in particular. (See "Same birthday as you" below for an analysis of this much less surprising alternative problem.)In the example given earlier, a list of 23 people, comparing the birthday of the first person on the list to the others allows 22 chances for a matching birthday (The second person on the list to the others allows 21 chances for a matching birthday, third person has 20 chances, and so on. Hence 22+21+20+....+1 = 253), but comparing every person to all of the others allows 253 distinct chances (combination
Combination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
s): in a group of 23 people there are
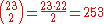 pairs.
pairs.Presuming all birthdays are equally probable, the probability of a given birthday for a person chosen from the entire population at random is 1/365 (ignoring Leap Day, February 29). Although the pairings in a group of 23 people are not statistically equivalent to 253 pairs chosen independently, the birthday paradox becomes less surprising if a group is thought of in terms of the number of possible pairs, rather than as the number of individuals.
Calculating the probability
The problem is to compute the approximate probability that in a room of n people, at least two have the same birthday. For simplicity, disregard variations in the distribution, such as leap yearLeap year
A leap year is a year containing one extra day in order to keep the calendar year synchronized with the astronomical or seasonal year...
s, twin
Twin
A twin is one of two offspring produced in the same pregnancy. Twins can either be monozygotic , meaning that they develop from one zygote that splits and forms two embryos, or dizygotic because they develop from two separate eggs that are fertilized by two separate sperm.In contrast, a fetus...
s, seasonal or weekday variations, and assume that the 365 possible birthdays are equally likely. Real-life birthday distributions are not uniform since not all dates are equally likely.
If P(A) is the probability of at least two people in the room having the same birthday, it may be simpler to calculate P(A
In deference to widely published solutions concluding that 23 is the number of people necessary to have a P(A) that is greater than 50%, the following calculation of P(A) will use 23 people as an example.
When events are independent of each other, the probability of all of the events occurring is equal to a product of the probabilities of each of the events occurring. Therefore, if P(A') can be described as 23 independent events, P(A
The 23 independent events correspond to the 23 people, and can be defined in order. Each event can be defined as the corresponding person not sharing their birthday with any of the previously analyzed people. For Event 1, there are no previously analyzed people. Therefore, the probability, P(1), that person number 1 does not share his/her birthday with previously analyzed people is 1, or 100%. Ignoring leap years for this analysis, the probability of 1 can also be written as 365/365, for reasons that will become clear below.
For Event 2, the only previously analyzed people are Person 1. Assuming that birthdays are equally likely to happen on each of the 365 days of the year, the probability, P(2), that Person 2 has a different birthday than Person 1 is 364/365. This is because, if Person 2 was born on any of the other 364 days of the year, Persons 1 and 2 will not share the same birthday.
Similarly, if Person 3 is born on any of the 363 days of the year other than the birthdays of Persons 1 and 2, Person 3 will not share their birthday. This makes the probability P(3) = 363/365.
This analysis continues until Person 23 is reached, whose probability of not sharing their birthday with people analyzed before, P(23), is 343/365.
P(A
- (1) P(A
' ) = 365/365 × 364/365 × 363/365 × 362/365 × ... × 343/365
The terms of equation (1) can be collected to arrive at:
- (2) P(A
' ) = (1/365)23 × (365 × 364 × 363 × ... × 343)
Evaluating equation (2) gives P(A
Therefore, P(A) = 1 − 0.492703 = 0.507297 (50.7297%)
This process can be generalized to a group of n people, where p(n) is the probability of at least two of the n people sharing a birthday. It is easier to first calculate the probability p(n) that all n birthdays are different. According to the pigeonhole principle, p(n) is zero when n > 365. When n ≤ 365:
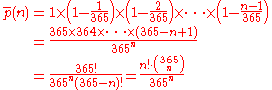
where ' ! ' is the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
operator.
The equation expresses the fact that for no persons to share a birthday, a second person cannot have the same birthday as the first (364/365), the third cannot have the same birthday as the first two (363/365), and in general the nth birthday cannot be the same as any of the n − 1 preceding birthdays.
The event
Event (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
of at least two of the n persons having the same birthday is complementary
Complementary event
In probability theory, the complement of any event A is the event [not A], i.e. the event that A does not occur. The event A and its complement [not A] are mutually exclusive and exhaustive. Generally, there is only one event B such that A and B are both mutually exclusive and...
to all n birthdays being different. Therefore, its probability p(n) is
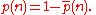
This probability surpasses 1/2 for n = 23 (with value about 50.7%). The following table shows the probability for some other values of n (this table ignores the existence of leap years, as described above):
| n | p(n) |
|---|---|
| 10 | 11.7% |
| 20 | 41.1% |
| 23 | 50.7% |
| 30 | 70.6% |
| 50 | 97.0% |
| 57 | 99.0% |
| 100 | 99.99997% |
| 200 | 99.9999999999999999999999999998% |
| 300 | (100 − (6×10−80))% |
| 350 | (100 − (3×10−129))% |
| 365 | (100 − (1.45×10−155))% |
| 366 | 100% |
Approximations
The Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
(the constant e = 2.718281828, approximately)
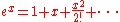
provides a first-order approximation for ex for x << 1:

The first expression derived for p(n) can be approximated as
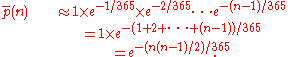
Therefore,
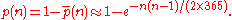
An even coarser approximation is given by
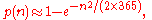
which, as the graph illustrates, is still fairly accurate.
A simple exponentiation
The probability of any two people not having the same birthday is 364/365. In a room containing n people, there are C(n, 2)=n(n-1)/2 pairs of people, i.e. C(n, 2) events. The probability of no two people sharing the same birthday can be approximated by assuming that these events are independent and hence by multiplying their probability together. In short 364/365 can be multiplied by itself C(n, 2) times, which gives us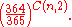
And if this is the probability of no one having the same birthday, then the probability of someone sharing a birthday is
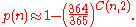
Poisson approximation
Using the PoissonPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
approximation for the binomial,
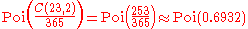
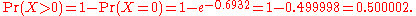
Again, this is over 50%.
Approximation of number of people
This can also be approximated using the following formula for the number of people necessary to have at least a 50% chance of matching:
This is a result of the good approximation that an event with 1 in k probability will have a 50% chance of occurring at least once if it is repeated k ln 2 times.
Probability table
| length of hex string |
#bits | hash space size (2#bits) |
Number of hashed elements such that (probability of at least one hash collision) = p | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p = 10−18 | p = 10−15 | p = 10−12 | p = 10−9 | p = 10−6 | p = 0.1% | p = 1% | p = 25% | p = 50% | p = 75% | |||
| 8 | 32 | 4.3 × 109 | 2 | 2 | 2 | 2.9 | 93 | 2.9 × 103 | 9.3 × 103 | 5.0 × 104 | 7.7 × 104 | 1.1 × 105 |
| 16 | 64 | 1.8 × 1019 | 6.1 | 1.9 × 102 | 6.1 × 103 | 1.9 × 105 | 6.1 × 106 | 1.9 × 108 | 6.1 × 108 | 3.3 × 109 | 5.1 × 109 | 7.2 × 109 |
| 32 | 128 | 3.4 × 1038 | 2.6 × 1010 | 8.2 × 1011 | 2.6 × 1013 | 8.2 × 1014 | 2.6 × 1016 | 8.3 × 1017 | 2.6 × 1018 | 1.4 × 1019 | 2.2 × 1019 | 3.1 × 1019 |
| 64 | 256 | 1.2 × 1077 | 4.8 × 1029 | 1.5 × 1031 | 4.8 × 1032 | 1.5 × 1034 | 4.8 × 1035 | 1.5 × 1037 | 4.8 × 1037 | 2.6 × 1038 | 4.0 × 1038 | 5.7 × 1038 |
| (96) | (384) | (3.9 × 10115) | 8.9 × 1048 | 2.8 × 1050 | 8.9 × 1051 | 2.8 × 1053 | 8.9 × 1054 | 2.8 × 1056 | 8.9 × 1056 | 4.8 × 1057 | 7.4 × 1057 | 1.0 × 1058 |
| 128 | 512 | 1.3 × 10154 | 1.6 × 1068 | 5.2 × 1069 | 1.6 × 1071 | 5.2 × 1072 | 1.6 × 1074 | 5.2 × 1075 | 1.6 × 1076 | 8.8 × 1076 | 1.4 × 1077 | 1.9 × 1077 |
- The white squares in this table show the number of hashes needed to achieve the given probability of collision (column) given a hashspace of a certain size in bits (row). (Using the birthday analogy: the "hash space size"(row) would be "365 days", the "probability of collision"(column) would be "50%", and the "required number of people" would be "26"(row-col intersection).) One could of course also use this chart to determine the minimum hash size required (given upper bounds on the hashes and probability of error), or the probability of collision (for fixed number of hashes and probability of error).
For comparison, 10−18 to 10−15 is the uncorrectable bit error rate of a typical hard disk http://arxiv.org/abs/cs/0701166. In theory, MD5MD5The MD5 Message-Digest Algorithm is a widely used cryptographic hash function that produces a 128-bit hash value. Specified in RFC 1321, MD5 has been employed in a wide variety of security applications, and is also commonly used to check data integrity...
, 128 bits, should stay within that range until about 820 billion documents, even if its possible outputs are many more.
An upper bound
The argument below is adapted from an argument of Paul HalmosPaul Halmos
Paul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
.
As stated above, the probability that no two birthdays coincide is
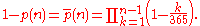
As in earlier paragraphs, interest lies in the smallest n such that p(n) > 1/2; or equivalently, the smallest n such that p(n) < 1/2.
Using the inequality 1 − x < e−x in the above expression we replace 1 − k/365 with e−k/365. This yields
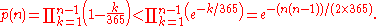
Therefore, the expression above is not only an approximation, but also an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
of p(n). The inequality

implies p(n) < 1/2. Solving for n gives

Now, 730 ln 2 is approximately 505.997, which is barely below 506, the value of n2 − n attained when n = 23. Therefore, 23 people suffice.
Solving n2 − n = 2 · 365 · ln 2 for n gives, by the way, the approximate formula of Frank H. Mathis cited above.
This derivation only shows that at most 23 people are needed to ensure a birthday match with even chance; it leaves open the possibility that, say, n = 22 could also work.
Cast as a collision problem
The birthday problem can be generalized as follows: given n random integers drawn from a discrete uniform distribution with range [1,d], what is the probability p(n;d) that at least two numbers are the same? (d=365 gives the usual birthday problem.)The generic results can be derived using the same arguments given above.

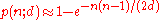

Conversely, if n(p;d) denotes the number of random integers drawn from [1,d] to obtain a probability p that at least two numbers are the same, then
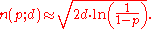
The birthday problem in this more generic sense applies to hash function
Hash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
s: the expected number of N-bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
hashes that can be generated before getting a collision is not 2N, but rather only 2N/2. This is exploited by birthday attack
Birthday attack
A birthday attack is a type of cryptographic attack that exploits the mathematics behind the birthday problem in probability theory. This attack can be used to abuse communication between two or more parties...
s on cryptographic hash function
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
s and is the reason why a small number of collisions in a hash table
Hash table
In computer science, a hash table or hash map is a data structure that uses a hash function to map identifying values, known as keys , to their associated values . Thus, a hash table implements an associative array...
are, for all practical purposes, inevitable.
The theory behind the birthday problem was used by Zoe Schnabel under the name of capture-recapture
Mark and recapture
Mark and recapture is a method commonly used in ecology to estimate population size. This method is most valuable when a researcher fails to detect all individuals present within a population of interest every time that researcher visits the study area...
statistics to estimate the size of fish population in lakes.
Generalization to multiple types
The basic problem considers all trials to be of one "type". The birthday problem has been generalized to consider an arbitrary number of types. In the simplest extension there are just two types, say m "men" and n "women", and the problem becomes characterizing the probability of a shared birthday between at least one man and one woman. (Shared birthdays between, say, two women do not count.) The probability of no (i.e. zero) shared birthdays here is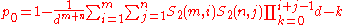
where d = 365 and S2 are Stirling numbers of the second kind
Stirling number
In mathematics, Stirling numbers arise in a variety of combinatorics problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second...
. Consequently, the desired probability is 1 − p0.
This variation of the birthday problem is interesting because there is not a unique solution for the total number of people m + n. For example, the usual 0.5 probability value is realized for both a 32-member group of 16 men and 16 women and a 49-member group of 43 women and 6 men.
Reverse problem
For a fixed probability p:- Find the greatest n for which the probability p(n) is smaller than the given p, or
- Find the smallest n for which the probability p(n) is greater than the given p.
Taking the above formula for d = 365 we have:
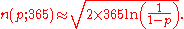
Sample calculations
| p | n | n↓ | p(n↓) | n↑ | p(n↑) |
|---|---|---|---|---|---|
| 0.01 | 0.14178√365 = 2.70864 | 2 | 0.00274 | 3 | 0.00820 |
| 0.05 | 0.32029√365 = 6.11916 | 6 | 0.04046 | 7 | 0.05624 |
| 0.1 | 0.45904√365 = 8.77002 | 8 | 0.07434 | 9 | 0.09462 |
| 0.2 | 0.66805√365 = 12.76302 | 12 | 0.16702 | 13 | 0.19441 |
| 0.3 | 0.84460√365 = 16.13607 | 16 | 0.28360 | 17 | 0.31501 |
| 0.5 | 1.17741√365 = 22.49439 | 22 | 0.47570 | 23 | 0.50730 |
| 0.7 | 1.55176√365 = 29.64625 | 29 | 0.68097 | 30 | 0.70632 |
| 0.8 | 1.79412√365 = 34.27666 | 34 | 0.79532 | 35 | 0.81438 |
| 0.9 | 2.14597√365 = 40.99862 | 40 | 0.89123 | 41 | 0.90315 |
| 0.95 | 2.44775√365 = 46.76414 | 46 | 0.94825 | 47 | 0.95477 |
| 0.99 | 3.03485√365 = 57.98081 | 57 | 0.99012 | 58 | 0.99166 |
Note: some values falling outside the bounds have been colored to show that the approximation is not always exact.
First match
A related question is, as people enter a room one at a time, which one is most likely to be the first to have the same birthday as someone already in the room? That is, for what n is p(n) − p(n − 1) maximum? The answer is 20—if there's a prize for first match, the best position in line is 20th.Same birthday as you
Note that in the birthday problem, neither of the two people is chosen in advance. By way of contrast, the probability q(n) that someone in a room of n other people has the same birthday as a particular person (for example, you), is given byand for general d by
In the standard case of d = 365 substituting n = 23 gives about 6.1%, which is less than 1 chance in 16. For a greater than 50% chance that one person in a roomful of n people has the same birthday as you, n would need to be at least 253. Note that this number is significantly higher than 365/2 = 182.5: the reason is that it is likely that there are some birthday matches among the other people in the room.
It is not a coincidence that
 ; a similar approximate pattern can be found using a number of possibilities different from 365, or a target probability different from 50%.
; a similar approximate pattern can be found using a number of possibilities different from 365, or a target probability different from 50%.Near matches
Another generalization is to ask how many people are needed in order to have a better than 50% chance that two people have a birthday within one day of each other, or within two, three, etc., days of each other. This is a more difficult problem and requires use of the inclusion-exclusion principleInclusion-exclusion principle
In combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
. The number of people required so that the probability that some pair will have a birthday separated by fewer than k days will be higher than 50% is:
| k | # people required |
|---|---|
| 1 | 23 |
| 2 | 14 |
| 3 | 11 |
| 4 | 9 |
| 5 | 8 |
| 6 | 8 |
| 7 | 7 |
| 8 | 7 |
Thus in a group of just seven random people, it is more likely than not that two of them will have a birthday within a week of each other.
Collision counting
The probability that the kth integer randomly chosen from [1, d] will repeat at least one previous choice equals q(k − 1; d) above. The expected total number of times a selection will repeat a previous selection as n such integers are chosen equals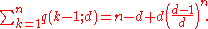
Average number of people
In an alternative formulation of the birthday problem, one asks the average number of people required to find a pair with the same birthday. The problem is relevant to several hashing algorithmsHash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
analyzed by Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
in his book The Art of Computer Programming
The Art of Computer Programming
The Art of Computer Programming is a comprehensive monograph written by Donald Knuth that covers many kinds of programming algorithms and their analysis....
. It may be shown that if one samples uniformly, with replacement, from a population of size M, the number of trials required for the first repeated sampling of some individual has expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
 , where
, whereThe function
has been studied by Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
and has asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
:
With M = 365 days in a year, the average number of people required to find a pair with the same birthday is
 , slightly more than the number required for a 50% chance. In the best case, two people will suffice; at worst, the maximum possible number of M + 1 = 366 people is needed; but on average
, slightly more than the number required for a 50% chance. In the best case, two people will suffice; at worst, the maximum possible number of M + 1 = 366 people is needed; but on averageAverage
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
, only 25 people are required.
An informal demonstration of the problem can be made from the list of Prime Ministers of Australia, in which Paul Keating
Paul Keating
Paul John Keating was the 24th Prime Minister of Australia, serving from 1991 to 1996. Keating was elected as the federal Labor member for Blaxland in 1969 and came to prominence as the reformist treasurer of the Hawke Labor government, which came to power at the 1983 election...
, the 24th Prime Minister, and Edmund Barton
Edmund Barton
Sir Edmund Barton, GCMG, KC , Australian politician and judge, was the first Prime Minister of Australia and a founding justice of the High Court of Australia....
, the first Prime Minister, share same birthday i.e. 18 January.
James K. Polk
James K. Polk
James Knox Polk was the 11th President of the United States . Polk was born in Mecklenburg County, North Carolina. He later lived in and represented Tennessee. A Democrat, Polk served as the 17th Speaker of the House of Representatives and the 12th Governor of Tennessee...
and Warren G. Harding
Warren G. Harding
Warren Gamaliel Harding was the 29th President of the United States . A Republican from Ohio, Harding was an influential self-made newspaper publisher. He served in the Ohio Senate , as the 28th Lieutenant Governor of Ohio and as a U.S. Senator...
, the 11th and 29th Presidents of the United States, were both born on November 2.
Sir John A. Macdonald
John A. Macdonald
Sir John Alexander Macdonald, GCB, KCMG, PC, PC , QC was the first Prime Minister of Canada. The dominant figure of Canadian Confederation, his political career spanned almost half a century...
and Jean Chrétien
Jean Chrétien
Joseph Jacques Jean Chrétien , known commonly as Jean Chrétien is a former Canadian politician who was the 20th Prime Minister of Canada. He served in the position for over ten years, from November 4, 1993 to December 12, 2003....
, the 1st and 20th Prime Ministers of Canada, were both born on January 11.
Of the 73 male actors to win the Academy Award for Best Actor
Academy Award for Best Actor
Performance by an Actor in a Leading Role is one of the Academy Awards of Merit presented annually by the Academy of Motion Picture Arts and Sciences to recognize an actor who has delivered an outstanding performance while working within the film industry...
, there are six pairs of actors who share the same birthday.
Of the 67 actresses to win the Academy Award for Best Actress
Academy Award for Best Actress
Performance by an Actress in a Leading Role is one of the Academy Awards of merit presented annually by the Academy of Motion Picture Arts and Sciences to recognize an actress who has delivered an outstanding performance while working within the film industry...
, there are three pairs of actresses who share the same birthday.
Of the 61 directors to win the Academy Award for Best Director, there are five pairs of directors who share the same birthday.
Of the 52 people to serve as Prime Minister of the United Kingdom
Prime Minister of the United Kingdom
The Prime Minister of the United Kingdom of Great Britain and Northern Ireland is the Head of Her Majesty's Government in the United Kingdom. The Prime Minister and Cabinet are collectively accountable for their policies and actions to the Sovereign, to Parliament, to their political party and...
, there are two pairs of men who share the same birthday.
Partition problem
A related problem is the partition problemPartition problem
In computer science, the partition problem is an NP-complete problem. The problem is to decide whether a given multiset of integers can be partitioned into two "halves" that have the same sum...
, a variant of the knapsack problem
Knapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
from operations research. Some weights are put on a balance scale
Weighing scale
A weighing scale is a measuring instrument for determining the weight or mass of an object. A spring scale measures weight by the distance a spring deflects under its load...
; each weight is an integer number of grams randomly chosen between one gram and one million grams (one metric ton). The question is whether one can usually (that is, with probability close to 1) transfer the weights between the left and right arms to balance the scale. (In case the sum of all the weights is an odd number of grams, a discrepancy of one gram is allowed.) If there are only two or three weights, the answer is very clearly no; although there are some combinations which work, the majority of randomly selected combinations of three weights do not. If there are very many weights, the answer is clearly yes. The question is, how many are just sufficient? That is, what is the number of weights such that it is equally likely for it to be possible to balance them as it is to be impossible?
Some people's intuition is that the answer is above 100,000. Most people's intuition is that it is in the thousands or tens of thousands, while others feel it should at least be in the hundreds. The correct answer is approximately 23.
The reason is that the correct comparison is to the number of partitions of the weights into left and right. There are 2N−1 different partitions for N weights, and the left sum minus the right sum can be thought of as a new random quantity for each partition. The distribution of the sum of weights is approximately Gaussian, with a peak at 1,000,000 N and width
 , so that when 2N−1 is approximately equal to
, so that when 2N−1 is approximately equal to  the transition occurs. 223−1 is about 4 million, while the width of the distribution is only 5 million.
the transition occurs. 223−1 is about 4 million, while the width of the distribution is only 5 million.External links
- Coincidences: the truth is out there Experimental test of the Birthday Paradox and other coincidences
- http://www.efgh.com/math/birthday.htm
- http://planetmath.org/encyclopedia/BirthdayProblem.html
- Maple vs. birthday paradox
- A humorous article explaining the paradox
- SOCR EduMaterials activities birthday experiment
- Understanding the Birthday Problem (Better Explained)