
Rational motion
Encyclopedia
In kinematics
, the motion of a rigid body
is defined as a continuous set of displacements. One-parameter motions can be defined
as a continuous displacement of moving object with respect to a fixed frame in Euclidean three-space (E3), where the displacement depends on one parameter, mostly identified as time.
Rational motions are defined by rational function
s (ratio of two polynomial functions) of time. They produce rational trajectories, and therefore they integrate well with the existing NURBS (Non-Uniform Rational B-Spline) based industry standard CAD/CAM systems. They are readily amenable to the applications of existing computer-aided geometric design
(CAGD) algorithms. By combining kinematics of rigid body motions with NURBS geometry of curves and surfaces, methods have been developed for computer-aided design
of rational motions.
These CAD methods for motion design find applications in animation
in computer graphics (key frame interpolation
), trajectory planning in robotics
(taught-position interpolation), spatial navigation in virtual reality
, computer-aided geometric design of motion via interactive interpolation, CNC tool path planning, and task specification in mechanism synthesis.
In recent years, it has been well established that rational Bezier
and rational B-spline
based curve representation schemes can be combined with dual quaternion
representation of spatial displacements to obtain rational Bezier and B-spline
motions. Ge and Ravani, developed a new framework for geometric constructions
of spatial motions by combining the concepts from kinematics and CAGD. Their work was built upon the seminal paper of Shoemake, in which he
used the concept of a quaternion
for rotation
interpolation. A detailed list of references on this topic can be found in and.

denote a unit dual quaternion. A homogeneous dual quaternion may be
written as a pair of quaternions, ; where
; where 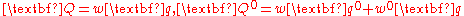 . This is obtained by
. This is obtained by
expanding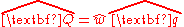 using
using
dual number
algebra (here,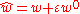 ).
).
In terms of dual quaternions and the homogeneous coordinates
of a point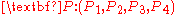 of the object, the transformation equation in terms of quaternions is given by (see for details)
of the object, the transformation equation in terms of quaternions is given by (see for details)
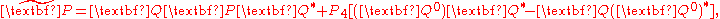
where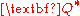 and
and 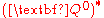 are
are
conjugates of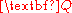 and
and 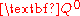 , respectively and
, respectively and
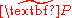 denotes homogeneous coordinates of the point
denotes homogeneous coordinates of the point
after the displacement.
Given a set of unit dual quaternions and dual weights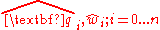 respectively, the
respectively, the
following represents a rational Bezier curve in the space of
dual quaternions.

where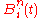 are the Bernstein polynomials. The Bezier dual quaternion curve given by above equation defines a rational Bezier motion of
are the Bernstein polynomials. The Bezier dual quaternion curve given by above equation defines a rational Bezier motion of
degree .
.
Similarly, a B-spline dual quaternion curve, which defines a NURBS
motion of degree 2p, is given by,
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
, the motion of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
is defined as a continuous set of displacements. One-parameter motions can be defined
as a continuous displacement of moving object with respect to a fixed frame in Euclidean three-space (E3), where the displacement depends on one parameter, mostly identified as time.
Rational motions are defined by rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s (ratio of two polynomial functions) of time. They produce rational trajectories, and therefore they integrate well with the existing NURBS (Non-Uniform Rational B-Spline) based industry standard CAD/CAM systems. They are readily amenable to the applications of existing computer-aided geometric design
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
(CAGD) algorithms. By combining kinematics of rigid body motions with NURBS geometry of curves and surfaces, methods have been developed for computer-aided design
Computer-aided design
Computer-aided design , also known as computer-aided design and drafting , is the use of computer technology for the process of design and design-documentation. Computer Aided Drafting describes the process of drafting with a computer...
of rational motions.
These CAD methods for motion design find applications in animation
Animation
Animation is the rapid display of a sequence of images of 2-D or 3-D artwork or model positions in order to create an illusion of movement. The effect is an optical illusion of motion due to the phenomenon of persistence of vision, and can be created and demonstrated in several ways...
in computer graphics (key frame interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
), trajectory planning in robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
(taught-position interpolation), spatial navigation in virtual reality
Virtual reality
Virtual reality , also known as virtuality, is a term that applies to computer-simulated environments that can simulate physical presence in places in the real world, as well as in imaginary worlds...
, computer-aided geometric design of motion via interactive interpolation, CNC tool path planning, and task specification in mechanism synthesis.
Background
There has been a great deal of research in applying the principles of computer-aided geometric design (CAGD) to the problem of computer-aided motion design.In recent years, it has been well established that rational Bezier
Bézier curve
A Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
and rational B-spline
Nonuniform rational B-spline
Non-uniform rational basis spline is a mathematical model commonly used in computer graphics for generating and representing curves and surfaces which offers great flexibility and precision for handling both analytic and freeform shapes.- History :Development of NURBS began in the 1950s by...
based curve representation schemes can be combined with dual quaternion
Dual quaternion
The set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual...
representation of spatial displacements to obtain rational Bezier and B-spline
motions. Ge and Ravani, developed a new framework for geometric constructions
of spatial motions by combining the concepts from kinematics and CAGD. Their work was built upon the seminal paper of Shoemake, in which he
used the concept of a quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
for rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
interpolation. A detailed list of references on this topic can be found in and.
Rational Bezier and B-spline motions
Let
denote a unit dual quaternion. A homogeneous dual quaternion may be
written as a pair of quaternions,
 ; where
; where 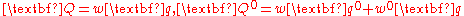 . This is obtained by
. This is obtained byexpanding
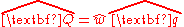 using
usingdual number
Dual number
In linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
algebra (here,
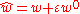 ).
).In terms of dual quaternions and the homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
of a point
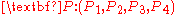 of the object, the transformation equation in terms of quaternions is given by (see for details)
of the object, the transformation equation in terms of quaternions is given by (see for details)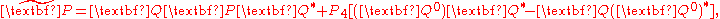
where
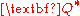 and
and 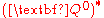 are
areconjugates of
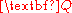 and
and 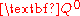 , respectively and
, respectively and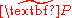 denotes homogeneous coordinates of the point
denotes homogeneous coordinates of the pointafter the displacement.
Given a set of unit dual quaternions and dual weights
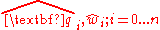 respectively, the
respectively, thefollowing represents a rational Bezier curve in the space of
dual quaternions.

where
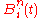 are the Bernstein polynomials. The Bezier dual quaternion curve given by above equation defines a rational Bezier motion of
are the Bernstein polynomials. The Bezier dual quaternion curve given by above equation defines a rational Bezier motion ofdegree
 .
.Similarly, a B-spline dual quaternion curve, which defines a NURBS
motion of degree 2p, is given by,
-
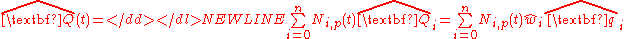
where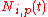 are the pth-degree B-spline basis functions.
are the pth-degree B-spline basis functions.
A representation for the rational Bezier motion and rational B-spline motion in the Cartesian space can be obtained by substituting either of the above two preceding expressions for in the equation for point transform. In what follows, we deal with the case of rational Bezier motion. The, the trajectory of a point undergoing rational Bezier motion is given by,
in the equation for point transform. In what follows, we deal with the case of rational Bezier motion. The, the trajectory of a point undergoing rational Bezier motion is given by,
-
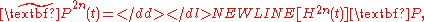
-

where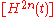 is the matrix
is the matrix
representation of the rational Bezier motion of degree
 in Cartesian space. The following matrices
in Cartesian space. The following matrices
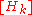 (also referred to as Bezier Control
(also referred to as Bezier Control
Matrices) define the affine control structure of the motion:
-
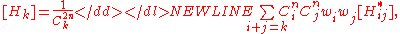
where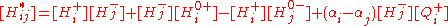 .
.
In the above equations, and
and 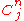
are binomial coefficients and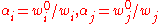 are the weight ratios and
are the weight ratios and
-

-

-

-

-

In above matrices,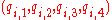
are four components of the real part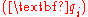 and
and
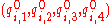 are four
are four
components of the dual part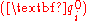 of the unit
of the unit
dual quaternion .
.
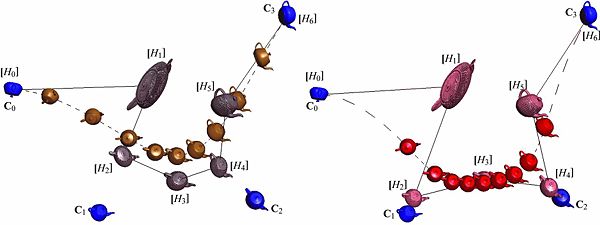
Example
External links
- Computational Design Kinematics Lab
- Robotics and Spatial Systems Laboratory (RASSL)
- Robotics and Automation Laboratory
See also
- QuaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
and Dual quaternionDual quaternionThe set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual... - NURBS
- Computer animationComputer animationComputer animation is the process used for generating animated images by using computer graphics. The more general term computer generated imagery encompasses both static scenes and dynamic images, while computer animation only refers to moving images....
- RoboticsRoboticsRobotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
- Robot kinematicsRobot kinematicsRobot kinematics is the study of the motion of robots. In a kinematic analysis the position, velocity and acceleration of all the links are calculated without considering the forces that cause this motion. The relationship between motion, and the associated forces and torques is studied in robot...
- Computational geometryComputational geometryComputational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
- CNC machining
- Mechanism designMechanism designMechanism design is a field in game theory studying solution concepts for a class of private information games...
-
-
-
-
-
-
-
-

