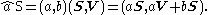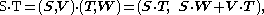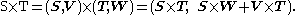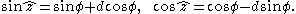Screw theory
Encyclopedia
Screw theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies.
The conceptual framework was developed by Sir Robert Stawell Ball
in 1876 for application in kinematics
and statics
of mechanism
s (rigid body mechanics).
The value of screw theory derives from the central role that the geometry of lines plays in three dimensional mechanics, where lines form the screw axes of spatial movement and the lines of action of forces. The pair of vectors that form the Plücker coordinates
of a line define a unit screw, and general screws are obtained by multiplication by a pair of real numbers and addition of vectors.
A remarkable result of screw theory is that geometric calculations for points using vectors have parallel geometric calculations for lines obtained by replacing vectors with screws. This is termed the transfer principle.
Screw theory notes that all rigid-body motion can be represented as rotation about an axis along with translation along the same axis; this axis need not be coincident with the object or particle undergoing displacement. In this framework, screw theory expresses displacements, velocities, forces, and torques in three dimensional space.
Recently screw theory has become an important tool in robot mechanics, mechanical design, computational geometry
and multibody dynamics.
This is in part because of the relationship between screws and dual quaternion
s which have been used to interpolate rigid-body motions. Based on screw theory, an efficient approach has also been developed for the type synthesis of parallel mechanisms (parallel manipulators or parallel robots)
Fundamental theorems include Poinsot's theorem (Louis Poinsot
, 1806) and Chasles' theorem (Michel Chasles
, 1832). Other prominent contributors include Julius Plücker
, W. K. Clifford
, F. M. Dimentberg, Kenneth H. Hunt
, J. R. Phillips.
that define the rotation and the three components of the translation vector.
The points in a body undergoing a constant screw motion trace helices in the fixed frame. If this screw motion has zero pitch then the trajectories trace circles, and the movement is a pure rotation. If the screw motion has infinite pitch then the trajectories are all straight lines in the same direction.
Now, introduce the ordered pair of real numbers â=(a, b) called dual scalars. Let the addition and subtraction of these numbers be componentwise, and define multiplication as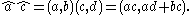
The multiplication of a screw S=(S, V) by the dual scalar â=(a, b) is computed componentwise to be,
Finally, introduce the dot and cross products of screws by the formulas:
and
The dot and cross products of screws satisfy the identities of vector algebra, and allow computations that directly parallel computations in the algebra of vectors.
Let the dual scalar ẑ=(φ, d) define a dual angle, then the infinite series definitions of sine and cosine yield the relations
In general, the function of a dual variable is defined to be f(ẑ)=(f(φ), df′(φ)), where f′(φ) is the derivative of f(φ).
These definitions allow the following results:
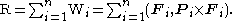
Notice that the case of two equal but opposite forces F and -F acting at points A and B respectively, yields the resultant R=(F-F, A×F - B× F) = (0, (A-B)×F). This shows that screws of the form M=(0, M) can be interpreted as pure moments.
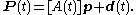
The velocity of P is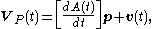
where v is velocity of the origin of the moving frame, that is dd/dt. Now substitute p= [AT](P-d) into this equation to obtain,
where [Ω]=[dA/dt][AT] is the angular velocity matrix and ω is the angular velocity vector.
The screw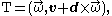
is the twist of the moving body. The vector V=v + d×ω is the velocity of the point in the body that corresponds with the origin of the fixed frame.
There are two important special cases: (i) when d is constant, that is v=0, then the twist is a pure rotation about the line L=(ω, d×ω), and (ii) when [Ω]=0, that is the body does not rotate but only slides in the direction v, then the twist is a pure slide given by L=(0, v).
Let the displacement of a body be defined by D=([A], d), where [A] is the rotation matrix and d is the translation vector. Consider the line in the body defined by the two points p and q, which has the Plücker coordinates
,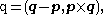
then in the fixed frame we have the transformed point coordinates P=[A]p+d and Q=[A]q+d, which yield.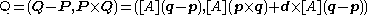
Thus, a spatial displacement defines a transformation for Plücker coordinates of lines given by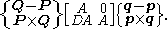
The matrix [D] is the skew symmetric matrix that performs the cross product operation, that is [D]y=d×y.
The 6×6 matrix [Â]=([A], [DA]) obtained from the spatial displacement D=([A], d) operates on a screw s=(s.v) to obtain: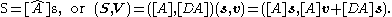
The dual matrix [Â]=([A], [DA]) has determinant 1 and is called a dual orthogonal matrix.
In screw notation velocity twists transform with a 6x6 transformation matrix
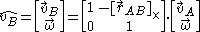
Where:
define a helical field called the force wrench. To move representation from point A to point B, once must account for the forces on the body such that:
In screw notation force wrenches transform with a 6x6 transformation matrix
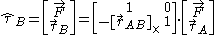
Where:
 , and a twist
, and a twist 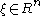 , the homogeneous transformation to a new location and orientation can be computed with the following formula:
, the homogeneous transformation to a new location and orientation can be computed with the following formula:
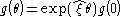
where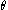 represents the parameters of the transformation.
represents the parameters of the transformation.
, given the axis of revolution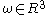 and a point
and a point 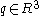 on that axis, the twist for the joint can be calculated with the following formula:
on that axis, the twist for the joint can be calculated with the following formula:
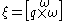
, given a vector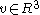 pointing in the direction of translation, the twist for the joint can be calculated with the following formula:
pointing in the direction of translation, the twist for the joint can be calculated with the following formula:
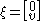
, the elemental concept of transformation is the reflection (mathematics)
. In planar transformations a translation is obtained by reflection in parallel lines, and rotation is obtained by reflection in a pair of intersecting lines. To produce a screw transformation from similar concepts one must use planes in space
: the parallel planes must be perpendicular to the screw axis
, which is the line of intersection of the intersecting planes that generate the rotation of the screw. Thus four reflections in planes effect a screw transformation. The tradition of inversive geometry borrows some of the ideas of projective geometry
and provides a language of transformation that does not depend on analytic geometry
.
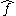 acting on a rigid body moving with a twist
acting on a rigid body moving with a twist
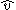 are reciprocal if the motion generated no power
are reciprocal if the motion generated no power
against the force:
The conceptual framework was developed by Sir Robert Stawell Ball
Robert Stawell Ball
Sir Robert Stawell Ball was an Irish astronomer. He worked for Lord Rosse from 1865 to 1867. In 1867 he became Professor of Applied Mathematics at the Royal College of Science in Dublin. In 1874 Ball was appointed Royal Astronomer of Ireland and Andrews Professor of Astronomy in the University...
in 1876 for application in kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
and statics
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
of mechanism
Mechanism (engineering)
A mechanism is a device designed to transform input forces and movement into a desired set of output forces and movement. Mechanisms generally consist of moving components such as gears and gear trains, belt and chain drives, cam and follower mechanisms, and linkages as well as friction devices...
s (rigid body mechanics).
The value of screw theory derives from the central role that the geometry of lines plays in three dimensional mechanics, where lines form the screw axes of spatial movement and the lines of action of forces. The pair of vectors that form the Plücker coordinates
Plücker coordinates
In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogenous coordinates to each line in projective 3-space, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines...
of a line define a unit screw, and general screws are obtained by multiplication by a pair of real numbers and addition of vectors.
A remarkable result of screw theory is that geometric calculations for points using vectors have parallel geometric calculations for lines obtained by replacing vectors with screws. This is termed the transfer principle.
Screw theory notes that all rigid-body motion can be represented as rotation about an axis along with translation along the same axis; this axis need not be coincident with the object or particle undergoing displacement. In this framework, screw theory expresses displacements, velocities, forces, and torques in three dimensional space.
Recently screw theory has become an important tool in robot mechanics, mechanical design, computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
and multibody dynamics.
This is in part because of the relationship between screws and dual quaternion
Dual quaternion
The set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual...
s which have been used to interpolate rigid-body motions. Based on screw theory, an efficient approach has also been developed for the type synthesis of parallel mechanisms (parallel manipulators or parallel robots)
Fundamental theorems include Poinsot's theorem (Louis Poinsot
Louis Poinsot
Louis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...
, 1806) and Chasles' theorem (Michel Chasles
Michel Chasles
Michel Floréal Chasles was a French mathematician.He was born at Épernon in France and studied at the École Polytechnique in Paris under Siméon Denis Poisson. In the War of the Sixth Coalition he was drafted to fight in the defence of Paris in 1814...
, 1832). Other prominent contributors include Julius Plücker
Julius Plücker
Julius Plücker was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves.- Early...
, W. K. Clifford
W. K. Clifford
W. K. Clifford may refer to:*William Kingdon Clifford, British mathematician and philosopher*Lucy Clifford Mrs W. K. Clifford, wife of the above, British novelist and journalist...
, F. M. Dimentberg, Kenneth H. Hunt
Kenneth H. Hunt
Kenneth Henderson Hunt was Foundation Professor of Engineering at Monash University in Melbourne, Australia and an expert in kinematics.Hunt was born in Seaford, East Sussex, in the United Kingdom, on 7 June 1920. He studied engineering at Balliol College, Oxford University and, during World War...
, J. R. Phillips.
Basic concepts
Here we describe screw, twist, and wrench in general terms, and save the mathematics for the following sections.Screw
A spatial displacement of a rigid body can be defined by a rotation about a line and a translation along the same line, called a screw displacement. This is known as Chasles' theorem. The six parameters that define a screw displacement are the four independent components of the Plucker vector that defines the screw axis, together with the rotation angle about and linear slide along this line, and form a pair of vectors called a screw. For comparison, the six parameters that define a spatial displacement can also be given by three Euler AnglesEuler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
that define the rotation and the three components of the translation vector.
The points in a body undergoing a constant screw motion trace helices in the fixed frame. If this screw motion has zero pitch then the trajectories trace circles, and the movement is a pure rotation. If the screw motion has infinite pitch then the trajectories are all straight lines in the same direction.
Twist
A twist represents the velocity of a rigid body as an angular velocity around an axis and a linear velocity along this axis. All points in the body have the same component of the velocity along the axis, however the greater the distance from the axis the greater the velocity in the plane perpendicular to this axis. Thus, the helicoidal field formed by the velocity vectors in a moving rigid body flattens out the further the points are radially from the twist axis.Wrench
The force and torque vectors that arise in applying Newton's laws to a rigid body can be assembled into a screw called a wrench. A force has a point of application and a line of action, therefore it defines the Plucker coordinates of a line in space and has zero pitch. A torque, on the other hand, is a pure moment that is not bound to a line in space and is an infinite pitch screw.Algebra of Screws
Let a screw be an ordered pair S=(S, V), where S and V are three dimensional real vectors. The sum and difference of these ordered pairs are computed componentwise. Screws are often called dual vectors.Now, introduce the ordered pair of real numbers â=(a, b) called dual scalars. Let the addition and subtraction of these numbers be componentwise, and define multiplication as
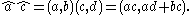
The multiplication of a screw S=(S, V) by the dual scalar â=(a, b) is computed componentwise to be,
Finally, introduce the dot and cross products of screws by the formulas:
and
The dot and cross products of screws satisfy the identities of vector algebra, and allow computations that directly parallel computations in the algebra of vectors.
Let the dual scalar ẑ=(φ, d) define a dual angle, then the infinite series definitions of sine and cosine yield the relations
In general, the function of a dual variable is defined to be f(ẑ)=(f(φ), df′(φ)), where f′(φ) is the derivative of f(φ).
These definitions allow the following results:
- Unit screws are Plucker coordinates of a line and satisfy the relation
-
-
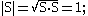
- Let ẑ=(φ, d) be the dual angle, where φ is the angle between the axes of S and T around their common normal, and d is the distance between these axes along the common normal, then
-
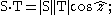
- Let N be the unit screw that defines the common normal to the axes of S and T, and ẑ=(φ, d) is the dual angle between these axes, then
-

-
Wrench
A common example of a screw is the wrench associated with a force acting on a rigid body. Let P be the point of application of the force F and let P be the vector locating this point in a fixed frame. The wrench W=(F, P×F) is a screw. The resultant force and moment obtained from all the forces Fi i=1,...,n, acting on a rigid body is simply the sum of the individual wrenches Wi, that is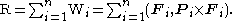
Notice that the case of two equal but opposite forces F and -F acting at points A and B respectively, yields the resultant R=(F-F, A×F - B× F) = (0, (A-B)×F). This shows that screws of the form M=(0, M) can be interpreted as pure moments.
Twist
In order to define the twist of a rigid body, we must consider its movement defined by the parameterized set of spatial displacements, D(t)=([A(f)],d(f)), where [A] is a rotation matrix and d is a translation vector. This causes a point p that is fixed in moving body to trace a curve P(t) in the fixed frame given by,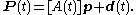
The velocity of P is
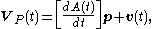
where v is velocity of the origin of the moving frame, that is dd/dt. Now substitute p= [AT](P-d) into this equation to obtain,

where [Ω]=[dA/dt][AT] is the angular velocity matrix and ω is the angular velocity vector.
The screw
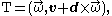
is the twist of the moving body. The vector V=v + d×ω is the velocity of the point in the body that corresponds with the origin of the fixed frame.
There are two important special cases: (i) when d is constant, that is v=0, then the twist is a pure rotation about the line L=(ω, d×ω), and (ii) when [Ω]=0, that is the body does not rotate but only slides in the direction v, then the twist is a pure slide given by L=(0, v).
Screws and spatial displacements
The coordinate transformations for screws are easily understood by beginning with the coordinate transformations of the Plücker vector of line, which in turn are obtained from the transformations of the coordinate of points on the line.Let the displacement of a body be defined by D=([A], d), where [A] is the rotation matrix and d is the translation vector. Consider the line in the body defined by the two points p and q, which has the Plücker coordinates
Plücker coordinates
In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogenous coordinates to each line in projective 3-space, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines...
,
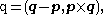
then in the fixed frame we have the transformed point coordinates P=[A]p+d and Q=[A]q+d, which yield.
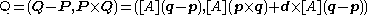
Thus, a spatial displacement defines a transformation for Plücker coordinates of lines given by
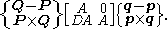
The matrix [D] is the skew symmetric matrix that performs the cross product operation, that is [D]y=d×y.
The 6×6 matrix [Â]=([A], [DA]) obtained from the spatial displacement D=([A], d) operates on a screw s=(s.v) to obtain:
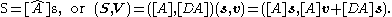
The dual matrix [Â]=([A], [DA]) has determinant 1 and is called a dual orthogonal matrix.
Twists
The velocities of each particle within a rigid body define a helical field called the velocity twist. To move representation from point A to point B, one must account for the rotation of the body such that:In screw notation velocity twists transform with a 6x6 transformation matrix
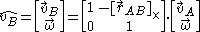
Where:
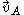 denotes the linear velocity at point A
denotes the linear velocity at point A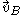 denotes the linear velocity at point B
denotes the linear velocity at point B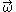 denotes the angular velocity of the rigid body
denotes the angular velocity of the rigid body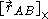 denotes the 3×3 cross product matrix
denotes the 3×3 cross product matrix
Wrenches
Similarly the equipolent moments expressed at each location within a rigid bodyRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
define a helical field called the force wrench. To move representation from point A to point B, once must account for the forces on the body such that:
In screw notation force wrenches transform with a 6x6 transformation matrix
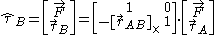
Where:
 denotes the equipollent (link: wikibooks.org ) moment at point A
denotes the equipollent (link: wikibooks.org ) moment at point A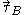 denotes the equipollent (link: wikibooks.org ) moment at point B
denotes the equipollent (link: wikibooks.org ) moment at point B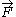 denotes the total force applied to the rigid body
denotes the total force applied to the rigid body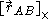 denotes the 3×3 cross product matrix
denotes the 3×3 cross product matrix
Twists as general displacements
Given an initial configuration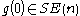 , and a twist
, and a twist 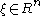 , the homogeneous transformation to a new location and orientation can be computed with the following formula:
, the homogeneous transformation to a new location and orientation can be computed with the following formula: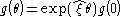
where
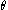 represents the parameters of the transformation.
represents the parameters of the transformation.Revolute Joints
For a revolute jointRevolute joint
A revolute joint is a one degree of freedom kinematic pair used in mechanisms. Revolute joints provide single-axis rotation function used in many places such as door hinges, folding mechanisms, and other uni-axial rotation devices. -See also:* Cylindrical joint* Kinematics* Degrees of freedom *...
, given the axis of revolution
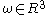 and a point
and a point 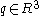 on that axis, the twist for the joint can be calculated with the following formula:
on that axis, the twist for the joint can be calculated with the following formula: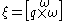
Prismatic Joints
For a prismatic jointPrismatic joint
A prismatic joint provides a linear sliding movement between two bodies, and is often called a slider, as in the slider-crank linkage. A prismatic joint is formed with a polygonal cross-section to resist rotation...
, given a vector
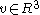 pointing in the direction of translation, the twist for the joint can be calculated with the following formula:
pointing in the direction of translation, the twist for the joint can be calculated with the following formula: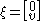
Screws by reflection
In transformation geometryTransformation geometry
In mathematics, transformation geometry is a name for a pedagogic theory for teaching Euclidean geometry, based on the Erlangen programme. Felix Klein, who pioneered this point of view, was himself interested in mathematical education. It took many years, though, for his "modern" point of view to...
, the elemental concept of transformation is the reflection (mathematics)
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
. In planar transformations a translation is obtained by reflection in parallel lines, and rotation is obtained by reflection in a pair of intersecting lines. To produce a screw transformation from similar concepts one must use planes in space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
: the parallel planes must be perpendicular to the screw axis
Screw axis
The screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
, which is the line of intersection of the intersecting planes that generate the rotation of the screw. Thus four reflections in planes effect a screw transformation. The tradition of inversive geometry borrows some of the ideas of projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
and provides a language of transformation that does not depend on analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
.
Reciprocity of twist and wrench
A wrench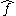 acting on a rigid body moving with a twist
acting on a rigid body moving with a twist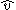 are reciprocal if the motion generated no power
are reciprocal if the motion generated no poweragainst the force:
-
See also
- Screw axisScrew axisThe screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
- Newton-Euler Equations uses screws to describe rigid body motions and loading.
External links
- Joe Rooney William Kingdon Clifford, Department of Design and Innovation, the Open University, London.
- Screw axis