Conversion between quaternions and Euler angles
Encyclopedia
Spatial rotations in three dimensions
can be parametrized
using both Euler angles
and unit quaternions
. This article explains how to convert between the two representations. Actually this simple use of "quaternions" was first presented by Euler
some seventy years earlier than Hamilton
to solve the problem of magic square
s. For this reason the dynamics community commonly refers to quaternions in this application as "Euler parameters".
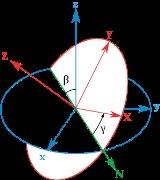
can be described as:
We can associate a quaternion
with a rotation around an axis by the following expression
where α is a simple rotation angle (the value in radians of the angle of rotation
) and cos(βx), cos(βy) and cos(βz) are the "direction cosines" locating the axis of rotation (Euler's Theorem).
The orthogonal matrix
(post-multiplying a column vector) corresponding to a clockwise/left-handed
rotation by the unit quaternion
is given by the inhomogeneous expression
or equivalently, by the homogeneous
expression
If
is not a unit quaternion then the homogeneous form is still a scalar multiple of a rotation matrix, while the inhomogeneous form is in general no longer an orthogonal matrix. This is why in numerical work the homogeneous form is to be preferred if distortion is to be avoided.
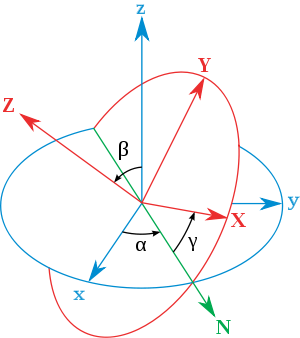
The orthogonal matrix
(post-multiplying a column vector) corresponding to a clockwise/left-handed
rotation with Euler angles
φ, θ, ψ, with x-y-z convention, is given by:
For Euler angles we get:
arctan and arcsin have a result between −π/2 and π/2
. With three rotations between −π/2 and π/2 you can't have all possible orientations. You need to replace the arctan by atan2
to generate all the orientations.
):
where the X-axis points forward, Y-axis to the right and Z-axis downward and in the example to follow the rotation occurs in the order yaw, pitch, roll (about body-fixed axes).
.
Code to handle the singularities is derived on this site: www.euclideanspace.com
Rotation representation (mathematics)
In geometry a rotation representation expresses a rotation as a mathematical transformation. In physics, this concept extends to classical mechanics where rotational kinematics is the science of describing with numbers the purely rotational motion of an object.According to Euler's rotation theorem...
can be parametrized
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
using both Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
and unit quaternions
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
. This article explains how to convert between the two representations. Actually this simple use of "quaternions" was first presented by Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
some seventy years earlier than Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
to solve the problem of magic square
Magic square
In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...
s. For this reason the dynamics community commonly refers to quaternions in this application as "Euler parameters".
Definition
A unit quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
can be described as:
We can associate a quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
with a rotation around an axis by the following expression
where α is a simple rotation angle (the value in radians of the angle of rotation
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
) and cos(βx), cos(βy) and cos(βz) are the "direction cosines" locating the axis of rotation (Euler's Theorem).
Rotation matrices
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(post-multiplying a column vector) corresponding to a clockwise/left-handed
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
rotation by the unit quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
is given by the inhomogeneous expressionor equivalently, by the homogeneous
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
expression
If
is not a unit quaternion then the homogeneous form is still a scalar multiple of a rotation matrix, while the inhomogeneous form is in general no longer an orthogonal matrix. This is why in numerical work the homogeneous form is to be preferred if distortion is to be avoided.The orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(post-multiplying a column vector) corresponding to a clockwise/left-handed
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
rotation with Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
φ, θ, ψ, with x-y-z convention, is given by:
Conversion
By combining the quaternion representations of the Euler rotations we getFor Euler angles we get:
arctan and arcsin have a result between −π/2 and π/2
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
. With three rotations between −π/2 and π/2 you can't have all possible orientations. You need to replace the arctan by atan2
Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
to generate all the orientations.
Relationship with Tait–Bryan angles
Similarly for Euler angles, we use the Tait–Bryan angles (in terms of flight dynamicsFlight dynamics
Flight dynamics is the science of air vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of mass, known as pitch, roll and yaw .Aerospace engineers develop control systems for...
):
- Roll –
: rotation about the X-axis - Pitch –
: rotation about the Y-axis - Yaw –
: rotation about the Z-axis
where the X-axis points forward, Y-axis to the right and Z-axis downward and in the example to follow the rotation occurs in the order yaw, pitch, roll (about body-fixed axes).
Singularities
One must be aware of singularities in the Euler angle parametrization when the pitch approaches ±90° (north/south pole). These cases must be handled specially. The common name for this situation is gimbal lockGimbal lock
Gimbal lock is the loss of one degree of freedom in a three-dimensional space that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space....
.
Code to handle the singularities is derived on this site: www.euclideanspace.com
See also
- Rotation operator (vector space)Rotation operator (vector space)This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
- Quaternions and spatial rotationQuaternions and spatial rotationUnit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
- Euler AnglesEuler anglesThe Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
- Rotation matrix
- Rotation representation (mathematics)Rotation representation (mathematics)In geometry a rotation representation expresses a rotation as a mathematical transformation. In physics, this concept extends to classical mechanics where rotational kinematics is the science of describing with numbers the purely rotational motion of an object.According to Euler's rotation theorem...