Orbital speed
Encyclopedia
The orbital speed of a body, generally a planet
, a natural satellite
, an artificial satellite
, or a multiple star
, is the speed at which it orbit
s around the barycenter
of a system, usually around a more mass
ive body. It can be used to refer to either the mean orbital speed, the average speed as it completes an orbit, or instantaneous orbital speed, the speed at a particular point in its orbit.
The orbital speed at any position in the orbit can be computed from the distance to the central body at that position, and the specific orbital energy
, which is independent of position: the kinetic energy
is the total energy minus the potential energy
.
, or equivalently, Kepler
's second law
. This states that as a body moves around its orbit during a fixed amount of time, the line from the barycenter to the body sweeps a constant area of the orbital plane, regardless of which part of its orbit the body traces during that period of time. This means that the body moves faster near its periapsis than near its apoapsis, because at the smaller distance it needs to trace a greater arc to cover the same area. This law is usually stated as "equal areas in equal time."
is close to that of a circular one, and the mean orbital speed can be approximated either from observations of the orbital period
and the semimajor axis of its orbit, or from knowledge of the mass
es of the two bodies and the semimajor axis.
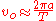
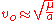
where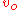
is the orbital velocity, 
is the length
of the semimajor axis,
is the orbital period, and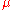 
is the standard gravitational parameter
. Note that this is only an approximation that holds true when the orbiting body is of considerably lesser mass than the central one, and eccentricity is close to zero.
Taking into account the mass of the orbiting body,
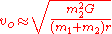
where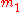
is now the mass of the body under consideration, 
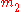is the mass of the body being orbited, 
is specifically the distance between the two bodies (which is the sum of the distances from each to the center of mass), and 
is the gravitational constant
. This is still a simplified version; it doesn't allow for elliptical
orbits, but it does at least allow for bodies of similar masses.
When one of the masses is almost negligible compared to the other mass as the case for Earth
and Sun
, one can approximate the previous formula to get:
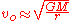
or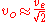
Where M is the (greater) mass around which this negligible mass or body is orbiting, and ve is the escape velocity
.
For an object in an eccentric orbit orbiting a much larger body, the length of the orbit decreases with eccentricity
, and is given at ellipse.
This can be used to obtain a more accurate estimate of the average orbital speed:
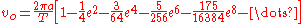
The mean orbital speed decreases with eccentricity.
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
, a natural satellite
Natural satellite
A natural satellite or moon is a celestial body that orbits a planet or smaller body, which is called its primary. The two terms are used synonymously for non-artificial satellites of planets, of dwarf planets, and of minor planets....
, an artificial satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
, or a multiple star
Multiple star
A multiple star consists of three or more stars which appear from the Earth to be close to one another in the sky. This may result from the stars being physically close and gravitationally bound to each other, in which case it is physical, or this closeness may be merely apparent, in which case...
, is the speed at which it orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s around the barycenter
Barycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
of a system, usually around a more mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
ive body. It can be used to refer to either the mean orbital speed, the average speed as it completes an orbit, or instantaneous orbital speed, the speed at a particular point in its orbit.
The orbital speed at any position in the orbit can be computed from the distance to the central body at that position, and the specific orbital energy
Specific orbital energy
In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
, which is independent of position: the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
is the total energy minus the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
.
Radial trajectories
In the case of radial motion:- If the energy is non-negative: The orbit is open. The motion is either directly towards or away from the other body, the motion never stops or reverses direction. See radial hyperbolic trajectory
- For the zero-energy case, see radial parabolic trajectory.
- If the energy is negative: The orbit is closed. The motion can be first away from the central body, up to r=μ/|ε| (apoapsis), then falling back. This is the limit case of an orbit which is part of an ellipse with eccentricity tending to 1, and the other end of the ellipse tending to the center of the central body. See radial elliptic trajectory, radial trajectories, free-fall timeFree-fall timeThe free-fall time is the characteristic time that would take a body to collapse under its own gravitational attraction, if no other forces existed to oppose the collapse...
.
Transverse orbital speed
The transverse orbital speed is inversely proportional to the distance to the central body because of the law of conservation of angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, or equivalently, Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
's second law
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
. This states that as a body moves around its orbit during a fixed amount of time, the line from the barycenter to the body sweeps a constant area of the orbital plane, regardless of which part of its orbit the body traces during that period of time. This means that the body moves faster near its periapsis than near its apoapsis, because at the smaller distance it needs to trace a greater arc to cover the same area. This law is usually stated as "equal areas in equal time."
Mean orbital speed
For orbits with small eccentricity, the length of the orbitis close to that of a circular one, and the mean orbital speed can be approximated either from observations of the orbital period
Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
and the semimajor axis of its orbit, or from knowledge of the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
es of the two bodies and the semimajor axis.
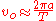
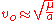
where
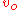is the orbital velocity, is the lengthLength
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
of the semimajor axis,
is the orbital period, and 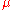is the standard gravitational parameterStandard gravitational parameter
In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
. Note that this is only an approximation that holds true when the orbiting body is of considerably lesser mass than the central one, and eccentricity is close to zero.
Taking into account the mass of the orbiting body,
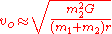
where
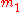is now the mass of the body under consideration, 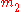is the mass of the body being orbited, is specifically the distance between the two bodies (which is the sum of the distances from each to the center of mass), and is the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
. This is still a simplified version; it doesn't allow for elliptical
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
orbits, but it does at least allow for bodies of similar masses.
When one of the masses is almost negligible compared to the other mass as the case for Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
and Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, one can approximate the previous formula to get:
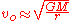
or
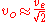
Where M is the (greater) mass around which this negligible mass or body is orbiting, and ve is the escape velocity
Escape velocity
In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...
.
For an object in an eccentric orbit orbiting a much larger body, the length of the orbit decreases with eccentricity
, and is given at ellipse.This can be used to obtain a more accurate estimate of the average orbital speed:
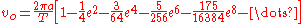
The mean orbital speed decreases with eccentricity.
See also
- Escape velocityEscape velocityIn physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...
- Delta-v budgetDelta-v budgetIn the astrodynamics and aerospace industry, a delta-v budget is the estimated delta-v requirements for the various propulsive tasks and orbital maneuvers over one or more phases of a space mission.Sample delta-v budget will enumerate various classes of maneuvers, delta-v per maneuver, number of...
- Hohmann transfer orbitHohmann transfer orbitIn orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits, typically both in the same plane....
- Bi-elliptic transferBi-elliptic transferIn astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer....