Delta-v
Overview
Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
a Δv or delta-v (literally "change in velocity") is a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
which takes units of speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
. It is a measure of the amount of "effort" that is needed to change from one trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
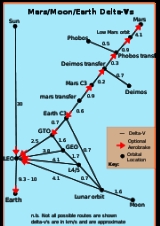
to another by making an orbital maneuver
Orbital maneuver
In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft.For spacecraft far from Earth—for example those in orbits around the Sun—an orbital maneuver is called a deep-space maneuver .-delta-v:...
.
Delta-v is produced by the use of propellant
Propellant
A propellant is a material that produces pressurized gas that:* can be directed through a nozzle, thereby producing thrust ;...
by reaction engines to produce a thrust that accelerates the vehicle.
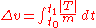
where
 is the instantaneous thrust
is the instantaneous thrustThrust
Thrust is a reaction force described quantitatively by Newton's second and third laws. When a system expels or accelerates mass in one direction the accelerated mass will cause a force of equal magnitude but opposite direction on that system....
 is the instantaneous mass
is the instantaneous massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
If there are no other external force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s than gravity, this is the integral of the magnitude of the g-force
G-force
The g-force associated with an object is its acceleration relative to free-fall. This acceleration experienced by an object is due to the vector sum of non-gravitational forces acting on an object free to move. The accelerations that are not produced by gravity are termed proper accelerations, and...
.
In the absence of external forces, and when thrust is applied in a constant direction this simplifies to:
which is simply the magnitude of the change in velocity
Delta-v (physics)
In general physics, delta-v is simply the change in velocity. The Greek letter delta is a standard mathematical symbol to represent change ....
.