
Orbit equation
Encyclopedia
In astrodynamics
an orbit
equation defines the path of orbiting body
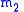 around central body
around central body
 relative to
relative to 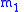 , without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance (such as gravity), has an orbit that is a conic section
, without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance (such as gravity), has an orbit that is a conic section
(i.e. circular orbit
, elliptic orbit
, parabolic trajectory
, hyperbolic trajectory
, or radial trajectory
) with the central body located at one of the two foci
, or the focus (Kepler's first law).
If the conic section intersects the central body, then the actual trajectory can only be the part above the surface, but for that part the orbit equation and many related formulas still apply, as long as it is a freefall (situation of weightlessness
).
In polar coordinates the orbit equation is: or
or 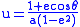
where we have the polar coordinates:
and the parameters:
Note that is the semi-latus rectum of the conic section. This ratio, together with , fully determines the geometry of the orbit. For a given orbit, the larger
, fully determines the geometry of the orbit. For a given orbit, the larger  , the faster the orbiting body moves in it: twice as fast if the attraction is four times as strong.
, the faster the orbiting body moves in it: twice as fast if the attraction is four times as strong.
The minimum value of r in the equation is
while, if , the maximum value is
, the maximum value is
If the maximum is less than the radius of the central body, then the conic section is an ellipse which is fully inside the central body and no part of it is a possible trajectory. If the maximum is more, but the minimum is less than the radius, part of the trajectory is possible:
If r becomes such that the orbiting body enters an atmosphere, then the standard assumptions no longer apply, as in atmospheric reentry
.
If the horizontal speed is , then the periapsis distance is . The energy at the surface of the Earth corresponds to that of an elliptic orbit with
, then the periapsis distance is . The energy at the surface of the Earth corresponds to that of an elliptic orbit with 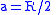 (with
(with  the radius of the Earth), which can not actually exist because it is an ellipse fully below the surface. The energy increase with increase of a is at a rate
the radius of the Earth), which can not actually exist because it is an ellipse fully below the surface. The energy increase with increase of a is at a rate 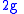 . The maximum height above the surface of the orbit is the length of the ellipse, minus
. The maximum height above the surface of the orbit is the length of the ellipse, minus  , minus the part "below" the center of the Earth, hence twice the increase of
, minus the part "below" the center of the Earth, hence twice the increase of  minus the periapsis distance. At the top the potential energy is
minus the periapsis distance. At the top the potential energy is  times this height, and the kinetic energy is . This adds up to the energy increase just mentioned. The width of the ellipse is 19 minutes times
times this height, and the kinetic energy is . This adds up to the energy increase just mentioned. The width of the ellipse is 19 minutes times  .
.
The part of the ellipse above the surface can be approximated by a part of a parabola, which is obtained in a model where gravity is assumed constant. This should be distinguished from the parabolic orbit in the sense of astrodynamics, where the velocity is the escape velocity
. See also trajectory
.
Note that in the sequence above, ,
,  and
and  increase monotonically, but
increase monotonically, but  first decreases from 1 to 0, then increases from 0 to infinity. The reversal is when the center of the Earth changes from apoapsis to periapsis (the other focus starts near the surface and passes the center of the Earth). We have
first decreases from 1 to 0, then increases from 0 to infinity. The reversal is when the center of the Earth changes from apoapsis to periapsis (the other focus starts near the surface and passes the center of the Earth). We have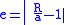
Extending this to orbits which are horizontal at another height, and orbits of which the extrapolation is horizontal below the surface of the Earth, we get a categorization of all orbits, except the radial trajectories, for which, by the way, the orbit equation can not be used. In this categorization ellipses are considered twice, so for ellipses with both sides above the surface one can restrict oneself to taking the side which is lower as the reference side, while for ellipses of which only one side is above the surface, taking that side.
Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
an orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
equation defines the path of orbiting body
Orbiting body
In astrodynamics, an orbiting body is a body that orbits a primary body .The orbiting body is properly referred to as the secondary body.It is less massive than the primary body ....
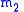 around central body
around central bodyCentral body
In astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
 relative to
relative to 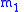 , without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance (such as gravity), has an orbit that is a conic section
, without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance (such as gravity), has an orbit that is a conic sectionConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
(i.e. circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
, elliptic orbit
Elliptic orbit
In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
, parabolic trajectory
Parabolic trajectory
In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1. When moving away from the source it is called an escape orbit, otherwise a capture orbit...
, hyperbolic trajectory
Hyperbolic trajectory
In astrodynamics or celestial mechanics a hyperbolic trajectory is a Kepler orbit with the eccentricity greater than 1. Under standard assumptions a body traveling along this trajectory will coast to infinity, arriving there with hyperbolic excess velocity relative to the central body. Similarly to...
, or radial trajectory
Radial trajectory
In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.- Classification :...
) with the central body located at one of the two foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
, or the focus (Kepler's first law).
If the conic section intersects the central body, then the actual trajectory can only be the part above the surface, but for that part the orbit equation and many related formulas still apply, as long as it is a freefall (situation of weightlessness
Weightlessness
Weightlessness is the condition that exists for an object or person when they experience little or no acceleration except the acceleration that defines their inertial trajectory, or the trajectory of pure free-fall...
).
In polar coordinates the orbit equation is:
 or
or 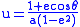
where we have the polar coordinates:
 is the distance between the orbiting body and the central bodyCentral bodyIn astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
is the distance between the orbiting body and the central bodyCentral bodyIn astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:... is the reciprocal distance (see the Binet's Equation http://scienceworld.wolfram.com/physics/BinetsEquation.html)
is the reciprocal distance (see the Binet's Equation http://scienceworld.wolfram.com/physics/BinetsEquation.html) is the direction of the orbiting body, called the true anomalyTrue anomalyIn celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
is the direction of the orbiting body, called the true anomalyTrue anomalyIn celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
and the parameters:
 is the specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
is the specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
of the orbiting body is the eccentricityEccentricity (mathematics)In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
is the eccentricityEccentricity (mathematics)In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
of the orbit, also called the orbital eccentricityOrbital eccentricityThe orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit... is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the orbit (taken negative for a hyperbola) is the constant which, divided by the distance squared, gives the magnitude of the acceleration; in the case of gravity this is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is the constant which, divided by the distance squared, gives the magnitude of the acceleration; in the case of gravity this is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
Note that is the semi-latus rectum of the conic section. This ratio, together with
 , fully determines the geometry of the orbit. For a given orbit, the larger
, fully determines the geometry of the orbit. For a given orbit, the larger  , the faster the orbiting body moves in it: twice as fast if the attraction is four times as strong.
, the faster the orbiting body moves in it: twice as fast if the attraction is four times as strong.The minimum value of r in the equation is

while, if
 , the maximum value is
, the maximum value is
If the maximum is less than the radius of the central body, then the conic section is an ellipse which is fully inside the central body and no part of it is a possible trajectory. If the maximum is more, but the minimum is less than the radius, part of the trajectory is possible:
- if the energy is non-negative (parabolic or hyperbolic orbit): the motion is either away from the central body, or towards it.
- if the energy is negative: the motion can be first away from the central body, up to
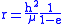
- after which the object falls back.
If r becomes such that the orbiting body enters an atmosphere, then the standard assumptions no longer apply, as in atmospheric reentry
Atmospheric reentry
Atmospheric entry is the movement of human-made or natural objects as they enter the atmosphere of a celestial body from outer space—in the case of Earth from an altitude above the Kármán Line,...
.
Low-energy trajectories
If the central body is the Earth, and the energy is only slightly larger than the potential energy at the surface of the Earth, then the orbit is elliptic with eccentricity close to 1 and one end of the ellipse just beyond the center of the Earth, and the other end just above the surface. Only a small part of the ellipse is applicable.If the horizontal speed is
 , then the periapsis distance is . The energy at the surface of the Earth corresponds to that of an elliptic orbit with
, then the periapsis distance is . The energy at the surface of the Earth corresponds to that of an elliptic orbit with 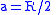 (with
(with  the radius of the Earth), which can not actually exist because it is an ellipse fully below the surface. The energy increase with increase of a is at a rate
the radius of the Earth), which can not actually exist because it is an ellipse fully below the surface. The energy increase with increase of a is at a rate 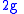 . The maximum height above the surface of the orbit is the length of the ellipse, minus
. The maximum height above the surface of the orbit is the length of the ellipse, minus  , minus the part "below" the center of the Earth, hence twice the increase of
, minus the part "below" the center of the Earth, hence twice the increase of  minus the periapsis distance. At the top the potential energy is
minus the periapsis distance. At the top the potential energy is  times this height, and the kinetic energy is . This adds up to the energy increase just mentioned. The width of the ellipse is 19 minutes times
times this height, and the kinetic energy is . This adds up to the energy increase just mentioned. The width of the ellipse is 19 minutes times  .
.The part of the ellipse above the surface can be approximated by a part of a parabola, which is obtained in a model where gravity is assumed constant. This should be distinguished from the parabolic orbit in the sense of astrodynamics, where the velocity is the escape velocity
Escape velocity
In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...
. See also trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
.
Categorization of orbits
Consider orbits which are at one point horizontal, near the surface of the Earth. For increasing speeds at this point the orbits are subsequently:- part of an ellipse with vertical major axis, with the center of the Earth as the far focus (throwing a stone, sub-orbital spaceflightSub-orbital spaceflightA sub-orbital space flight is a spaceflight in which the spacecraft reaches space, but its trajectory intersects the atmosphere or surface of the gravitating body from which it was launched, so that it does not complete one orbital revolution....
, ballistic missileBallistic missileA ballistic missile is a missile that follows a sub-orbital ballistic flightpath with the objective of delivering one or more warheads to a predetermined target. The missile is only guided during the relatively brief initial powered phase of flight and its course is subsequently governed by the...
) - a circle just above the surface of the Earth (Low Earth orbitLow Earth orbitA low Earth orbit is generally defined as an orbit within the locus extending from the Earth’s surface up to an altitude of 2,000 km...
) - an ellipse with vertical major axis, with the center of the Earth as the near focus
- a parabola
- a hyperbola
Note that in the sequence above,
 ,
,  and
and  increase monotonically, but
increase monotonically, but  first decreases from 1 to 0, then increases from 0 to infinity. The reversal is when the center of the Earth changes from apoapsis to periapsis (the other focus starts near the surface and passes the center of the Earth). We have
first decreases from 1 to 0, then increases from 0 to infinity. The reversal is when the center of the Earth changes from apoapsis to periapsis (the other focus starts near the surface and passes the center of the Earth). We have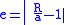
Extending this to orbits which are horizontal at another height, and orbits of which the extrapolation is horizontal below the surface of the Earth, we get a categorization of all orbits, except the radial trajectories, for which, by the way, the orbit equation can not be used. In this categorization ellipses are considered twice, so for ellipses with both sides above the surface one can restrict oneself to taking the side which is lower as the reference side, while for ellipses of which only one side is above the surface, taking that side.
See also
- Kepler's first law
- Circular orbitCircular orbitA circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
- Elliptic orbitElliptic orbitIn astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
- Parabolic trajectoryParabolic trajectoryIn astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1. When moving away from the source it is called an escape orbit, otherwise a capture orbit...
- Hyperbolic trajectoryHyperbolic trajectoryIn astrodynamics or celestial mechanics a hyperbolic trajectory is a Kepler orbit with the eccentricity greater than 1. Under standard assumptions a body traveling along this trajectory will coast to infinity, arriving there with hyperbolic excess velocity relative to the central body. Similarly to...
- Rocket equation

