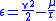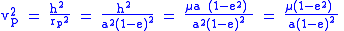Specific orbital energy
Encyclopedia
In the gravitational two-body problem
, the specific orbit
al energy (or vis-viva energy) of two orbiting bodies
(or vis-viva energy) of two orbiting bodies
is the constant sum of their mutual potential energy
( ) and their total kinetic energy
) and their total kinetic energy
(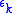 ), divided by the reduced mass
), divided by the reduced mass
. According to the orbital energy conservation equation (also referred to as vis-viva equation), it does not vary with time:

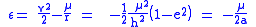
where
It is expressed in J/kg = m2s
−2 or
MJ/kg = km2s−2. For an elliptical orbit the specific orbital energy is the negative of the additional energy required to accelerate a mass of one kilogram to escape velocity
(parabolic orbit). For a hyperbolic orbit, it is equal to the excess energy compared to that of a parabolic orbit. In this case the specific orbital energy is also referred to as characteristic energy
.
at one of the orbit's apsides
, simplifies to:

where
Proof:
For a parabolic orbit this equation simplifies to
For a hyperbolic trajectory
this specific orbital energy is either given by

or the same as for an ellipse, depending on the convention for the sign of a.
In this case the specific orbital energy is also referred to as characteristic energy
(or ) and is equal to the excess specific energy compared to that for a parabolic orbit.
) and is equal to the excess specific energy compared to that for a parabolic orbit.
It is related to the hyperbolic excess velocity (the orbital velocity
(the orbital velocity
at infinity) by
It is relevant for interplanetary missions.
Thus, if orbital position vector ( ) and orbital velocity vector (
) and orbital velocity vector ( ) are known at one position, and
) are known at one position, and  is known, then the energy can be computed and from that, for any other position, the orbital speed.
is known, then the energy can be computed and from that, for any other position, the orbital speed.

where
In the case of circular orbits, this rate is one half of the gravity at the orbit. This corresponds to the fact that for such orbits the total energy is one half of the potential energy, because the kinetic energy is minus one half of the potential energy.

has an orbital period of 91.74 minutes, hence the semi-major axis is 6,738 km.
The energy is −29.6 MJ/kg: the potential energy is −59.2 MJ/kg, and the kinetic energy 29.6 MJ/kg. Compare with the potential energy at the surface, which is −62.6 MJ/kg. The extra potential energy is 3.4 MJ/kg, the total extra energy is 33.0 MJ/kg. The average speed is 7.7 km/s, the net delta-v
to reach this orbit is 8.1 km/s (the actual delta-v is typically 1.5–2 km/s more for atmospheric drag and gravity drag
).
The increase per meter would be 4.4 J/kg; this rate corresponds to one half of the local gravity of 8.8 m/s².
For an altitude of 100 km (radius is 6471 km):
The energy is −30.8 MJ/kg: the potential energy is −61.6 MJ/kg, and the kinetic energy 30.8 MJ/kg. Compare with the potential energy at the surface, which is −62.6 MJ/kg. The extra potential energy is 1.0 MJ/kg, the total extra energy is 31.8 MJ/kg.
The increase per meter would be 4.8 J/kg; this rate corresponds to one half of the local gravity of 9.5 m/s². The speed is 7.8 km/s, the net delta-v to reach this orbit is 8.0 km/s.
Taking into account the rotation of the Earth, the delta-v is up to 0.46 km/s less (starting at the equator and going east) or more (if going west).
, with respect to the Sun:
Hence:
Thus the hyperbolic excess velocity (the theoretical orbital velocity
at infinity) is given by 16.6 km/s
16.6 km/s
However, Voyager 1 does not have enough velocity to leave the Milky Way
. The computed speed applies far away from the Sun, but at such a position that the potential energy with respect to the Milky Way as a whole has changed negligibly, and only if there is no strong interaction with celestial bodies other than the Sun.
Then the time-rate of change of the specific energy of the rocket is : an amount
: an amount  for the kinetic energy and an amount
for the kinetic energy and an amount  for the potential energy.
for the potential energy.
The change of the specific energy of the rocket per unit change of delta-v is
which is |v| times the cosine of the angle between v and a.
Thus, when applying delta-v to increase specific orbital energy, this is done most efficiently if a is applied in the direction of v, and when |v| is large. If the angle between v and g is obtuse, for example in a launch and in a transfer to a higher orbit, this means applying the delta-v as early as possible and at full capacity. See also gravity drag
. When passing by a celestial body it means applying thrust when nearest to the body. When gradually making an elliptic orbit larger, it means applying thrust each time when near the periapsis.
When applying delta-v to decrease specific orbital energy, this is done most efficiently if a is applied in the direction opposite to that of v, and again when |v| is large. If the angle between v and g is acute, for example in a landing (on a celestial body without atmosphere) and in a transfer to a circular orbit around a celestial body when arriving from outside, this means applying the delta-v as late as possible. When passing by a planet it means applying thrust when nearest to the planet. When gradually making an elliptic orbit smaller, it means applying thrust each time when near the periapsis.
If a is in the direction of v:

Gravitational two-body problem
For further relevant mathematical developments see also Two-body problem, also Kepler orbit, and Kepler problem, and Equation of the center – Analytical expansions...
, the specific orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
al energy
 (or vis-viva energy) of two orbiting bodies
(or vis-viva energy) of two orbiting bodiesOrbiting body
In astrodynamics, an orbiting body is a body that orbits a primary body .The orbiting body is properly referred to as the secondary body.It is less massive than the primary body ....
is the constant sum of their mutual potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
(
 ) and their total kinetic energy
) and their total kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
(
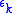 ), divided by the reduced mass
), divided by the reduced massReduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
. According to the orbital energy conservation equation (also referred to as vis-viva equation), it does not vary with time:

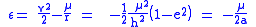
where
 is the relative orbital speedOrbital speedThe orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...
is the relative orbital speedOrbital speedThe orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...
; is the orbital distance between the bodies;
is the orbital distance between the bodies;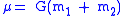 is the sum of the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is the sum of the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
s of the bodies; is the specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
is the specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
in the sense of relative angular momentum divided by the reduced mass; is the orbital eccentricity;
is the orbital eccentricity; is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
.
It is expressed in J/kg = m2s
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
−2 or
MJ/kg = km2s−2. For an elliptical orbit the specific orbital energy is the negative of the additional energy required to accelerate a mass of one kilogram to escape velocity
Escape velocity
In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...
(parabolic orbit). For a hyperbolic orbit, it is equal to the excess energy compared to that of a parabolic orbit. In this case the specific orbital energy is also referred to as characteristic energy
Characteristic energy
In astrodynamics a characteristic energy , a form of specific energy, is a measure of the energy required for an interplanetary mission that requires attaining an excess orbital velocity over an escape velocity required for additional orbital maneuvers...
.
Equation forms for different orbits
For an elliptical orbit, the specific orbital energy equation, when combined with conservation of specific angular momentumSpecific relative angular momentum
The specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
at one of the orbit's apsides
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
, simplifies to:

where
 is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
; is semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the orbit.
Proof:
-
- For an elliptical orbit with specific angular momentum h given by
-
- we use the general form of the specific orbital energy equation,
-
- with the relation that the relative velocity at periapsis is
-
- Thus our specific orbital energy equation becomes
-
- and finally with the last simplification we obtain:
For a parabolic orbit this equation simplifies to

For a hyperbolic trajectory
Hyperbolic trajectory
In astrodynamics or celestial mechanics a hyperbolic trajectory is a Kepler orbit with the eccentricity greater than 1. Under standard assumptions a body traveling along this trajectory will coast to infinity, arriving there with hyperbolic excess velocity relative to the central body. Similarly to...
this specific orbital energy is either given by

or the same as for an ellipse, depending on the convention for the sign of a.
In this case the specific orbital energy is also referred to as characteristic energy
Characteristic energy
In astrodynamics a characteristic energy , a form of specific energy, is a measure of the energy required for an interplanetary mission that requires attaining an excess orbital velocity over an escape velocity required for additional orbital maneuvers...
(or
 ) and is equal to the excess specific energy compared to that for a parabolic orbit.
) and is equal to the excess specific energy compared to that for a parabolic orbit.It is related to the hyperbolic excess velocity
 (the orbital velocity
(the orbital velocityOrbital velocity
Orbital velocity can refer to the following:* The orbital speed of a body in a gravitational field.* The velocity of particles due to wave motion, in particular in wind waves....
at infinity) by

It is relevant for interplanetary missions.
Thus, if orbital position vector (
 ) and orbital velocity vector (
) and orbital velocity vector ( ) are known at one position, and
) are known at one position, and  is known, then the energy can be computed and from that, for any other position, the orbital speed.
is known, then the energy can be computed and from that, for any other position, the orbital speed.Rate of change
For an elliptical orbit the rate of change of the specific orbital energy with respect to a change in the semi-major axis is
where
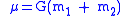 is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
; is semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the orbit.
In the case of circular orbits, this rate is one half of the gravity at the orbit. This corresponds to the fact that for such orbits the total energy is one half of the potential energy, because the kinetic energy is minus one half of the potential energy.
Additional energy
If the central body has radius R, then the additional energy of an elliptic orbit compared to being stationary at the surface is
- For the Earth and a just little more than
 this is
this is 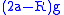 ; the quantity
; the quantity  is the height the ellipse extends above the surface, plus the periapsis distance (the distance the ellipse extends beyond the center of the Earth); the latter times g is the kinetic energy of the horizontal component of the velocity.
is the height the ellipse extends above the surface, plus the periapsis distance (the distance the ellipse extends beyond the center of the Earth); the latter times g is the kinetic energy of the horizontal component of the velocity.
ISS
The International Space StationInternational Space Station
The International Space Station is a habitable, artificial satellite in low Earth orbit. The ISS follows the Salyut, Almaz, Cosmos, Skylab, and Mir space stations, as the 11th space station launched, not including the Genesis I and II prototypes...
has an orbital period of 91.74 minutes, hence the semi-major axis is 6,738 km.
The energy is −29.6 MJ/kg: the potential energy is −59.2 MJ/kg, and the kinetic energy 29.6 MJ/kg. Compare with the potential energy at the surface, which is −62.6 MJ/kg. The extra potential energy is 3.4 MJ/kg, the total extra energy is 33.0 MJ/kg. The average speed is 7.7 km/s, the net delta-v
Delta-v
In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
to reach this orbit is 8.1 km/s (the actual delta-v is typically 1.5–2 km/s more for atmospheric drag and gravity drag
Gravity drag
In astrodynamics and rocketry, gravity drag is a measure of the loss in the net performance of a rocket while it is thrusting in a gravitational field...
).
The increase per meter would be 4.4 J/kg; this rate corresponds to one half of the local gravity of 8.8 m/s².
For an altitude of 100 km (radius is 6471 km):
The energy is −30.8 MJ/kg: the potential energy is −61.6 MJ/kg, and the kinetic energy 30.8 MJ/kg. Compare with the potential energy at the surface, which is −62.6 MJ/kg. The extra potential energy is 1.0 MJ/kg, the total extra energy is 31.8 MJ/kg.
The increase per meter would be 4.8 J/kg; this rate corresponds to one half of the local gravity of 9.5 m/s². The speed is 7.8 km/s, the net delta-v to reach this orbit is 8.0 km/s.
Taking into account the rotation of the Earth, the delta-v is up to 0.46 km/s less (starting at the equator and going east) or more (if going west).
Voyager 1
For Voyager 1Voyager 1
The Voyager 1 spacecraft is a 722-kilogram space probe launched by NASA in 1977, to study the outer Solar System and eventually interstellar space. Operating for as of today , the spacecraft receives routine commands and transmits data back to the Deep Space Network. At a distance of as of...
, with respect to the Sun:
 = 132,712,440,018 km3s−2 is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
= 132,712,440,018 km3s−2 is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
of the Sun- r = 17 billion1000000000 (number)1,000,000,000 is the natural number following 999,999,999 and preceding 1,000,000,001.In scientific notation, it is written as 109....
kilometers - v = 17.1 km/s
Hence:
-
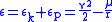 146 km2s−2 - 8 km2s−2 = 138 km2s−2
146 km2s−2 - 8 km2s−2 = 138 km2s−2
Thus the hyperbolic excess velocity (the theoretical orbital velocity
Orbital velocity
Orbital velocity can refer to the following:* The orbital speed of a body in a gravitational field.* The velocity of particles due to wave motion, in particular in wind waves....
at infinity) is given by
 16.6 km/s
16.6 km/sHowever, Voyager 1 does not have enough velocity to leave the Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
. The computed speed applies far away from the Sun, but at such a position that the potential energy with respect to the Milky Way as a whole has changed negligibly, and only if there is no strong interaction with celestial bodies other than the Sun.
Applying thrust
Assume:- a is the acceleration due to thrustThrustThrust is a reaction force described quantitatively by Newton's second and third laws. When a system expels or accelerates mass in one direction the accelerated mass will cause a force of equal magnitude but opposite direction on that system....
(the time-rate at which delta-vDelta-vIn astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
is spent) - g is the gravitational field strength
- v is the velocity of the rocket
Then the time-rate of change of the specific energy of the rocket is
 : an amount
: an amount  for the kinetic energy and an amount
for the kinetic energy and an amount  for the potential energy.
for the potential energy.The change of the specific energy of the rocket per unit change of delta-v is

which is |v| times the cosine of the angle between v and a.
Thus, when applying delta-v to increase specific orbital energy, this is done most efficiently if a is applied in the direction of v, and when |v| is large. If the angle between v and g is obtuse, for example in a launch and in a transfer to a higher orbit, this means applying the delta-v as early as possible and at full capacity. See also gravity drag
Gravity drag
In astrodynamics and rocketry, gravity drag is a measure of the loss in the net performance of a rocket while it is thrusting in a gravitational field...
. When passing by a celestial body it means applying thrust when nearest to the body. When gradually making an elliptic orbit larger, it means applying thrust each time when near the periapsis.
When applying delta-v to decrease specific orbital energy, this is done most efficiently if a is applied in the direction opposite to that of v, and again when |v| is large. If the angle between v and g is acute, for example in a landing (on a celestial body without atmosphere) and in a transfer to a circular orbit around a celestial body when arriving from outside, this means applying the delta-v as late as possible. When passing by a planet it means applying thrust when nearest to the planet. When gradually making an elliptic orbit smaller, it means applying thrust each time when near the periapsis.
If a is in the direction of v: