
Elliptic orbit
Encyclopedia

Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
or celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
an elliptic orbit is a Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
with the eccentricity
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
less than 1; this includes the special case of a circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 (thus excluding the circular orbit). In a wider sense it is a Kepler orbit with negative energy
Specific orbital energy
In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
. This includes the radial elliptic orbit, with eccentricity equal to 1.
In a gravitational two-body problem
Gravitational two-body problem
For further relevant mathematical developments see also Two-body problem, also Kepler orbit, and Kepler problem, and Equation of the center – Analytical expansions...
with negative energy both bodies follow similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
elliptic orbits with the same orbital period
Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
around their common barycenter
Barycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
. Also the relative position of one body with respect to the other follows an elliptic orbit.
Examples of elliptic orbits include: Hohmann transfer orbit
Hohmann transfer orbit
In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits, typically both in the same plane....
, Molniya orbit
Molniya orbit
Molniya orbit is a type of highly elliptical orbit with an inclination of 63.4 degrees, an argument of perigee of -90 degree and an orbital period of one half of a sidereal day...
and tundra orbit
Tundra orbit
Tundra orbit is a type of highly elliptical geosynchronous orbit with a high inclination and an orbital period of one sidereal day . A satellite placed in this orbit spends most of its time over a chosen area of the Earth, a phenomenon known as apogee dwell...
.
Velocity
Under standard assumptions the orbital speedOrbital speed
The orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...
(
 ) of a body traveling along elliptic orbit can be computed from the Vis-viva equation
) of a body traveling along elliptic orbit can be computed from the Vis-viva equationVis-viva equation
In astrodynamics, the vis viva equation, also referred to as orbital energy conservation equation, is one of the fundamental and useful equations that govern the motion of orbiting bodies....
as:
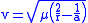
where:
 is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
, is the distance between the orbiting bodies.
is the distance between the orbiting bodies. is the length of the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is the length of the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
.
The velocity equation for a hyperbolic trajectory
Hyperbolic trajectory
In astrodynamics or celestial mechanics a hyperbolic trajectory is a Kepler orbit with the eccentricity greater than 1. Under standard assumptions a body traveling along this trajectory will coast to infinity, arriving there with hyperbolic excess velocity relative to the central body. Similarly to...
has either +
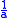 , or it is the same with the convention that in that case a is negative.
, or it is the same with the convention that in that case a is negative.Orbital period
Under standard assumptions the orbital periodOrbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
(
 ) of a body traveling along an elliptic orbit can be computed as:
) of a body traveling along an elliptic orbit can be computed as: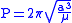
where:
 is standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
, is length of semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is length of semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
.
Conclusions:
- The orbital period is equal to that for a circular orbitCircular orbitA circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
with the orbit radius equal to the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
( ),
), - For a given semi-major axis the orbital period does not depend on the eccentricity (See also: Kepler's third law).
Energy
Under standard assumptions, specific orbital energySpecific orbital energy
In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
(
 ) of elliptic orbit is negative and the orbital energy conservation equation (the Vis-viva equation
) of elliptic orbit is negative and the orbital energy conservation equation (the Vis-viva equationVis-viva equation
In astrodynamics, the vis viva equation, also referred to as orbital energy conservation equation, is one of the fundamental and useful equations that govern the motion of orbiting bodies....
) for this orbit can take the form:
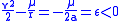
where:
 is orbital speedOrbital speedThe orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...
is orbital speedOrbital speedThe orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...
of orbiting body, is distance of orbiting body from central bodyCentral bodyIn astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
is distance of orbiting body from central bodyCentral bodyIn astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
, is length of semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is length of semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
, is standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
.
Conclusions:
- For a given semi-major axis the specific orbital energy is independent of the eccentricity.
Using the virial theorem we find:
- the time-average of the specific potential energy is equal to 2ε
- the time-average of r−1 is a−1
- the time-average of the specific kinetic energy is equal to –ε
Flight path angle
The flight path angle is the angle between the orbiting body's velocity vector (= the vector tangent to the instantaneous orbit) and the local horizontal. Under standard assumptions the flight path angle satisfies the equation:
satisfies the equation:
where:
 is the specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
is the specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
of the orbit, is orbital speedOrbital speedThe orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...
is orbital speedOrbital speedThe orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...
of orbiting body, is radial distance of orbiting body from central bodyCentral bodyIn astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
is radial distance of orbiting body from central bodyCentral bodyIn astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
, is the flight path angle
is the flight path angle
Orbital parameters
The state of an orbiting body at any given time is defined by the orbiting body's position and velocity with respect to the central body, which can be represented by the three-dimensional Cartesian coordinates (position of the orbiting body represented by x, y, and z) and the similar Cartesian components of the orbiting body's velocity. This set of six variables, together with time, are called the orbital state vectorsOrbital state vectors
In astrodynamics or celestial dynamics orbital state vectors are vectors of position and velocity that together with their time uniquely determine the state of an orbiting body....
. Given the masses of the two bodies they determine the full orbit. The two most general cases with these 6 degrees of freedom are the elliptic and the hyperbolic orbit. Special cases with less degrees of freedom are the circular and parabolic orbit.
Because at least six variables are absolutely required to completely represent an elliptic orbit with this set of parameters, then six variables are required to represent an orbit with any set of parameters. Another set of six parameters that are commonly used are the orbital elements
Orbital elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are generally considered in classical two-body systems, where a Kepler orbit is used...
.
Solar system
In the solar systemSolar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
, planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s, asteroid
Asteroid
Asteroids are a class of small Solar System bodies in orbit around the Sun. They have also been called planetoids, especially the larger ones...
s, most comet
Comet
A comet is an icy small Solar System body that, when close enough to the Sun, displays a visible coma and sometimes also a tail. These phenomena are both due to the effects of solar radiation and the solar wind upon the nucleus of the comet...
s and some pieces of space debris
Space debris
Space debris, also known as orbital debris, space junk, and space waste, is the collection of objects in orbit around Earth that were created by humans but no longer serve any useful purpose. These objects consist of everything from spent rocket stages and defunct satellites to erosion, explosion...
have approximately elliptical orbits around the Sun. Strictly speaking, both bodies revolve around the same focus of the ellipse, the one closer to the more massive body, but when one body is significantly more massive, as the sun vis-a-vis the earth, the focus may be contained within the larger massing body, and thus the smaller is said to revolve around it. The following chart of the perihelion and aphelion
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
of the planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s, dwarf planet
Dwarf planet
A dwarf planet, as defined by the International Astronomical Union , is a celestial body orbiting the Sun that is massive enough to be spherical as a result of its own gravity but has not cleared its neighboring region of planetesimals and is not a satellite...
s and Halley's Comet demonstrates the variation of the eccentricity of their elliptical orbits. For similar distances from the sun, wider bars denote greater eccentricity. Note the almost-zero eccentricity of Earth and Venus compared to the enormous eccentricity of Halley's Comet and Eris.
Radial elliptic trajectory
A radial trajectoryRadial trajectory
In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.- Classification :...
can be a double line segment, which is a degenerate ellipse with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1 this is not a parabolic orbit. Most properties and formulas of elliptic orbits apply. However, the orbit cannot be closed. It is an open orbit corresponding to the part of the degenerate ellipse from the moment the bodies touch each other and move away from each other until they touch each other again. In the case of point masses one full orbit is possible, starting and ending with a singularity. The velocities at the start and end are infinite in opposite directions, and the potential energy is equal to minus infinity.
The radial elliptic trajectory is the solution of a two-body problem with at some instant zero speed, as in the case of dropping an object (neglecting air resistance).
See also Free fall#Inverse-square law gravitational field.
History
Babylonian astronomers in the first millennium B.C.E. observed that the Sun's motion along the eclipticEcliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
was not uniform, though they were unaware of why this was; it is today known that this is due to the Earth moving in an elliptic orbit around the Sun, with the Earth moving faster when it is nearer to the Sun at perihelion and moving slower when it is farther away at aphelion.
In the 17th century, Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun at one focus, in his first law of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
. Later, Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
explained this as a corollary of his law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
.
See also
- Characteristic energyCharacteristic energyIn astrodynamics a characteristic energy , a form of specific energy, is a measure of the energy required for an interplanetary mission that requires attaining an excess orbital velocity over an escape velocity required for additional orbital maneuvers...
- EllipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
- List of orbits
- Orbital eccentricityOrbital eccentricityThe orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
- Orbital equation
- Parabolic trajectoryParabolic trajectoryIn astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1. When moving away from the source it is called an escape orbit, otherwise a capture orbit...
External links
- JAVA applet animating the orbit of a satellite in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.
- Apogee - Perigee Lunar photographic comparison
- Aphelion - Perihelion Solar photographic comparison
- http://www.castor2.ca/02_Armchair/02_Orbits/05_Tundra/index.html

