In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, an Hadamard space, named after Jacques Hadamard

Jacques Hadamard

Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...

, is a non-linear generalization of a Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

. It is defined to be a nonempty complete metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

 where, given any points x, y, there exists a point m such that for every point z,


The point m is then the midpoint of x and y: .

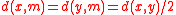In a Hilbert space, the above inequality is equality (with 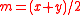), and in general an Hadamard space is said to be flat if the above inequality is equality. A flat Hadmard space is isomorphic to a closed convex subset of a Hilbert space. In particular, a normed space is an Hadamard space if and only if it is a Hilbert space.

The geometry of Hadamard spaces resemble that of Hilbert spaces, making it a natural setting for the study of rigidity theorems. In an Hadamard space, any two points can be joined by a unique geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

 between them; in particular, it is contractible

Contractible space

In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....

. Quite generally, if B is a bounded subset of a metric space, then the center of the closed ball of the minimum radius containing it is called the circumcenter of B. Every bounded subset of an Hadamard space is contained in the smallest closed ball (which is the same as the closure of its convex hull). If is the group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 of isometries

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

 of an Hadamard space leaving invariant B, then fixes the circumcenter of B. (Bruhat–Tits fixed point theorem)

The basic result for a non-positively curved manifold is the Cartan–Hadamard theorem

Cartan–Hadamard theorem

The Cartan–Hadamard theorem is a statement in Riemannian geometry concerning the structure of complete Riemannian manifolds of non-positive sectional curvature. The theorem states that the universal cover of such a manifold is diffeomorphic to a Euclidean space via the exponential map at any point...

. The analog holds for an Hadamard space: a complete, connected metric space which is locally isometric to an Hadamard space has an Hadamard space as its universal cover. Its variant applies for non-positively curved orbifold

Orbifold

In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...

s. (cf. Lurie.)

Examples of Hadamard spaces are Hilbert spaces, the Poincaré disc, trees (e.g., Bruhat–Tits building

Bruhat–Tits building

In mathematics, a building is a combinatorial and geometric structure which simultaneously generalizes certain aspects of flag manifolds, finite projective planes, and Riemannian symmetric spaces...

), Cayley graph

Cayley graph

In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...

s of discrete group

Discrete group

In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...

s, (p, q)-space with p, q ≥ 3 and 2pq ≥ p + q, and Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

s of nonpositive sectional curvature

Sectional curvature

In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...

 (e.g., symmetric space

Symmetric space

A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...

s). An Hadamard space is precisely a complete CAT(0) space

CAT(k) space

In mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...

.

See also

• Cartan–Tits fixed point theorem (this gives, for example, a conjugacy of maximal compact Lie subgroups of a real reductive group.)
• Metric topos