
Stokes boundary layer
Encyclopedia
In fluid dynamics
, the Stokes boundary layer, or oscillatory boundary layer, refers to the boundary layer
close to a solid wall in oscillatory
flow of a viscous
fluid
. Or, it refers to the similar case of an oscillating plate in a viscous fluid at rest, with the oscillation direction(s) parallel
to the plate.
For the case of laminar flow
at low Reynolds numbers over a smooth solid wall, George Gabriel Stokes
– after whom this boundary layer is called – derived an analytic solution, one of the few exact solutions for the Navier–Stokes equations.
In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments
, numerical simulations
or approximate methods
in order to obtain useful information on the flow.
The thickness
of the oscillatory boundary layer is called the Stokes boundary-layer thickness.
An important observation from Stokes' solution for the oscillating Stokes flow is, that vorticity oscillations are confined to a thin boundary layer and damp exponentially when moving away from the wall. This observation is also valid for the case of a turbulent boundary layer. Outside the Stokes boundary layer – which is often the bulk of the fluid volume – the vorticity oscillations may be neglected. To good approximation, the flow velocity oscillations are irrotational outside the boundary layer, and potential flow
theory can be applied to the oscillatory part of the motion. This significantly simplifies the solution of these flow problems, and is often applied in the irrotational flow regions of sound waves and water waves.
and parallel to the plane wall. The only non-zero velocity component is called u (SI
measure in meter/second
, or m/s) and is in the x-direction parallel to the oscillation direction. Moreover, since the flow is taken to be incompressible
, the velocity component u is only a function of time t (in seconds) and distance from the wall z (in meter). The Reynolds number is taken small enough for the flow to be laminar. Then the Navier–Stokes equations, without additional forcing, reduce to:
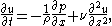
with:
and
Because the velocity u is not a function of position x along the plate, the pressure gradient ∂p/∂x is also independent of x (but the pressure p varies linear
ly with x). Moreover, the Navier–Stokes equation for the velocity component perpendicular to the wall reduces to ∂p/∂z = 0, so the pressure p and pressure gradient ∂p/∂x are also independent of the distance to the wall z. In conclusion, the pressure forcing ∂p/∂x can only be a function of time t.
The only non-zero component of the vorticity vector is the one in the direction perpendicular
to x and z, called ω (in s-1) and equal to:
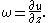
Taking the z-derivative of the above equation, ω has to satisfy
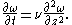
As usual for the vorticity dynamics, the pressure drops out of the vorticity equation.
, parallel to a plane rigid plate, will result in the fluid near the plate being dragged with the plate, due to the viscous shear stresses. Suppose the motion of the plate is
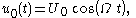
with
The plate, located at z = 0, forces the viscous fluid adjacent to have the same velocity u1( z, t ) resulting in the no-slip condition
:
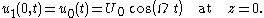
Far away from the plate, for z → ∞, the velocity u1 approaches zero. Consequently, the pressure gradient ∂p/∂x is zero at infinity and, since it is only a function of time t and not of z, has to be zero everywhere:
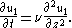
Such an equation is called a one-dimensional heat equation
or diffusion equation.
As a result, the solution for the flow velocity is
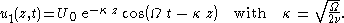
Here, κ is a kind of wavenumber
in the z-direction, associated with a length
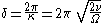
which is called the Stokes boundary-layer thickness. At a distance δ from the plate, the velocity amplitude has been reduced to e-2π ≈ 0.002 times its value U0 at the plate surface. Further, as can be seen from the phase changes Ω t - κ z in the solution u1, the velocity oscillations propagate as a damped wave
away from the wall, with wavelength
δ and phase speed Ω / κ.
The vorticity ω1 is equal to
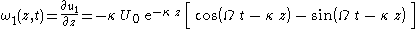
and, as u1, dampens exponentially in amplitude when moving away from the plate surface.
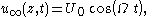
which satisfies the flow equations for the Stokes boundary layer, provided it is driven by a pressure gradient

Subtracting the solution u1( z, t ) from u∞( z, t ) gives the desired solution for an oscillating flow near a rigid wall at rest:
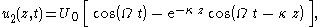
which is zero at the wall z = 0, corresponding with the no-slip condition for a wall at rest. Further the velocity u2 oscillates with amplitude U0 far away from the wall, z → ∞. This situation is often encountered in sound waves near a solid wall, or for the fluid motion near the sea bed in water waves.
The vorticity, for the oscillating flow near a wall at rest, is equal to the vorticity in case of an oscillating plate but of opposite sign: ω2 = - ω1.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Stokes boundary layer, or oscillatory boundary layer, refers to the boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
close to a solid wall in oscillatory
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
flow of a viscous
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
. Or, it refers to the similar case of an oscillating plate in a viscous fluid at rest, with the oscillation direction(s) parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to the plate.
For the case of laminar flow
Laminar flow
Laminar flow, sometimes known as streamline flow, occurs when a fluid flows in parallel layers, with no disruption between the layers. At low velocities the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross currents...
at low Reynolds numbers over a smooth solid wall, George Gabriel Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
– after whom this boundary layer is called – derived an analytic solution, one of the few exact solutions for the Navier–Stokes equations.
In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments
Flow measurement
Flow measurement is the quantification of bulk fluid movement. Flow can be measured in a variety of ways.Positive-displacement flow meters acumulate a fixed volume of fluid and then count the number of times the volume is filled to measure flow...
, numerical simulations
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
or approximate methods
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
in order to obtain useful information on the flow.
The thickness
Boundary-layer thickness
This page describes some parameters used to measure the properties of boundary layers. Consider a stationary body with a turbulent flow moving around it, like the semi-infinite flat plate with air flowing over the top of the plate...
of the oscillatory boundary layer is called the Stokes boundary-layer thickness.
An important observation from Stokes' solution for the oscillating Stokes flow is, that vorticity oscillations are confined to a thin boundary layer and damp exponentially when moving away from the wall. This observation is also valid for the case of a turbulent boundary layer. Outside the Stokes boundary layer – which is often the bulk of the fluid volume – the vorticity oscillations may be neglected. To good approximation, the flow velocity oscillations are irrotational outside the boundary layer, and potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
theory can be applied to the oscillatory part of the motion. This significantly simplifies the solution of these flow problems, and is often applied in the irrotational flow regions of sound waves and water waves.
Stokes boundary layer for laminar flow near a wall
The oscillating flow is assumed to be uni-directionalUni-directional
Unidirectional refers to an object that moves in only one direction at one time.It can refer to:*In communications theory, it is referred to as simplex communication or using ITU standards it refers to half-duplex signaling behavior....
and parallel to the plane wall. The only non-zero velocity component is called u (SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
measure in meter/second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
, or m/s) and is in the x-direction parallel to the oscillation direction. Moreover, since the flow is taken to be incompressible
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
, the velocity component u is only a function of time t (in seconds) and distance from the wall z (in meter). The Reynolds number is taken small enough for the flow to be laminar. Then the Navier–Stokes equations, without additional forcing, reduce to:
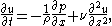
with:
- ρ the mass density of the fluid (kgKilogramThe kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
/m3), taken to be a constantConstant (mathematics)In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
, - p the fluid pressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
(SI: PaPascal (unit)The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
), - ν the kinematic viscosity of the fluid (m2/s), also taken constant.
and
- u the velocity of the fluid along the plate (m/s)
- x the position along the plate (m)
- z the distance from the plate (m)
- t the time (s)
Because the velocity u is not a function of position x along the plate, the pressure gradient ∂p/∂x is also independent of x (but the pressure p varies linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
ly with x). Moreover, the Navier–Stokes equation for the velocity component perpendicular to the wall reduces to ∂p/∂z = 0, so the pressure p and pressure gradient ∂p/∂x are also independent of the distance to the wall z. In conclusion, the pressure forcing ∂p/∂x can only be a function of time t.
The only non-zero component of the vorticity vector is the one in the direction perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to x and z, called ω (in s-1) and equal to:
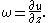
Taking the z-derivative of the above equation, ω has to satisfy
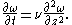
As usual for the vorticity dynamics, the pressure drops out of the vorticity equation.
Oscillation of a plane rigid plate
Harmonic motionHarmonic motion
Harmonic motion can mean:*The motion of a Harmonic oscillator , which can be:**Simple harmonic motion**Complex harmonic motion*Keplers laws of planetary motion...
, parallel to a plane rigid plate, will result in the fluid near the plate being dragged with the plate, due to the viscous shear stresses. Suppose the motion of the plate is
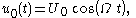
with
- U0 the velocity amplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the plate motion (in m/s), and - Ω the angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the motion (in radRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
/s).
The plate, located at z = 0, forces the viscous fluid adjacent to have the same velocity u1( z, t ) resulting in the no-slip condition
No-slip condition
In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.The fluid velocity at all fluid–solid boundaries is equal to that of the solid boundary...
:
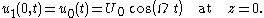
Far away from the plate, for z → ∞, the velocity u1 approaches zero. Consequently, the pressure gradient ∂p/∂x is zero at infinity and, since it is only a function of time t and not of z, has to be zero everywhere:
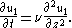
Such an equation is called a one-dimensional heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
or diffusion equation.
| Details on the derivation of the solution |
|---|
| This equation can be solved for harmonic motion using complex number Complex number A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part... s and separation of variables Separation of variables In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation.... : 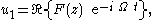 with i2 = -1 and ℜ{•} denoting the real part of the quantity between brackets. Then from the flow equation, F(z) is required to satisfy: 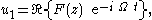 with the boundary conditions: 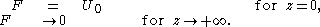 The solution for F(z) becomes: 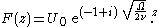 |
As a result, the solution for the flow velocity is
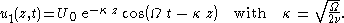
Here, κ is a kind of wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
in the z-direction, associated with a length
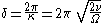
which is called the Stokes boundary-layer thickness. At a distance δ from the plate, the velocity amplitude has been reduced to e-2π ≈ 0.002 times its value U0 at the plate surface. Further, as can be seen from the phase changes Ω t - κ z in the solution u1, the velocity oscillations propagate as a damped wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
away from the wall, with wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
δ and phase speed Ω / κ.
The vorticity ω1 is equal to
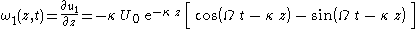
and, as u1, dampens exponentially in amplitude when moving away from the plate surface.
Flow due to an oscillating pressure gradient near a plane rigid plate
The case for an oscillating far-field flow, with the plate held at rest, can easily be constructed from the previous solution for an oscillating plate by using linear superposition of solutions. Consider a uniform velocity oscillation u∞: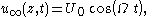
which satisfies the flow equations for the Stokes boundary layer, provided it is driven by a pressure gradient

Subtracting the solution u1( z, t ) from u∞( z, t ) gives the desired solution for an oscillating flow near a rigid wall at rest:
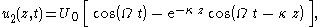
which is zero at the wall z = 0, corresponding with the no-slip condition for a wall at rest. Further the velocity u2 oscillates with amplitude U0 far away from the wall, z → ∞. This situation is often encountered in sound waves near a solid wall, or for the fluid motion near the sea bed in water waves.
The vorticity, for the oscillating flow near a wall at rest, is equal to the vorticity in case of an oscillating plate but of opposite sign: ω2 = - ω1.

