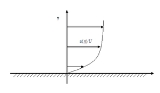
Blasius boundary layer
Encyclopedia
In physics
and fluid mechanics
, a Blasius boundary layer (named after Paul Richard Heinrich Blasius
) describes the steady two-dimensional boundary layer
that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow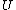 .
.
 The solution to the Navier–Stokes equation for this flow begins with an order-of-magnitude analysis to determine what terms are important. Within the boundary layer the usual balance between viscosity and convective inertia is struck, resulting in the scaling argument
The solution to the Navier–Stokes equation for this flow begins with an order-of-magnitude analysis to determine what terms are important. Within the boundary layer the usual balance between viscosity and convective inertia is struck, resulting in the scaling argument
 ,
,
where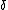 is the boundary-layer thickness and
is the boundary-layer thickness and  is the kinematic viscosity
is the kinematic viscosity
.
However the semi-infinite plate has no natural length scale and so the steady, incompressible, two-dimensional boundary-layer equations for continuity and momentum are
and so the steady, incompressible, two-dimensional boundary-layer equations for continuity and momentum are
Continuity: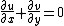
x-Momentum:
(note that the x-independence of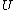 has been accounted for in the boundary-layer
has been accounted for in the boundary-layer
equations)
admit a similarity solution. In the system of partial differential equations written above it is assumed that a fixed solid body wall is parallel to the x-direction
whereas the y-direction is normal with respect to the fixed wall. and
and  denote here the x- and y-components of the fluid velocity vector.
denote here the x- and y-components of the fluid velocity vector.
Furthermore, from the scaling argument it is apparent that the boundary layer grows with the downstream coordinate , e.g.
, e.g.
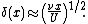
This suggests adopting the similarity variable

and writing
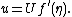
It proves convenient to work with the stream function
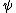 , in which case
, in which case

and on differentiating, to find the velocities, and substituting into the boundary-layer equation we obtain the Blasius equation
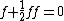
subject to
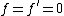 on
on 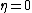 and
and
 as
as 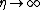 . This non-linear ODE can be solved numerically, with the shooting method
. This non-linear ODE can be solved numerically, with the shooting method
proving an effective choice.
The shear stress on the plate

can then be computed. The numerical solution gives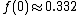 .
.
 from some uniform velocity field
from some uniform velocity field 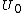 . We then estimate the outer flow to be of the form:
. We then estimate the outer flow to be of the form:
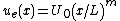
Where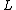 is a characteristic length and m is a dimensionless constant. In the Blasius solution, m = 0 corresponding to an angle of attack of zero radians. Thus we can write:
is a characteristic length and m is a dimensionless constant. In the Blasius solution, m = 0 corresponding to an angle of attack of zero radians. Thus we can write:
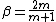
As in the Blasius solution, we use a similarity variable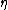 to solve the Navier-Stokes Equations.
to solve the Navier-Stokes Equations.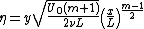
It becomes easier to describe this in terms of its stream function which we write as
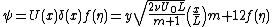
Thus the initial differential equation which was written as follows:
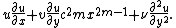
Can now be expressed in terms of the non-linear ODE known as the Falkner–Skan equation (named after V. M. Falkner and Sylvia W. Skan).
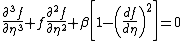
(note that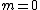 produces the Blasius equation). See Wilcox 2007.
produces the Blasius equation). See Wilcox 2007.
In 1937 Douglas Hartree
revealed that physical solutions exist only in the range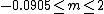 . Here, m<0 corresponds to an adverse pressure gradient (often resulting in boundary layer separation) while m > 0 represents a favorable pressure gradient.
. Here, m<0 corresponds to an adverse pressure gradient (often resulting in boundary layer separation) while m > 0 represents a favorable pressure gradient.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, a Blasius boundary layer (named after Paul Richard Heinrich Blasius
Paul Richard Heinrich Blasius
Paul Richard Heinrich Blasius was a German fluid dynamics engineer.He was one of the first students of Prandtl who provided a mathematical basis for boundary-layer drag but also showed as early as 1911 that the resistance to flow through smooth pipes could be expressed in terms of the Reynolds...
) describes the steady two-dimensional boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow
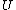 .
.
 ,
,where
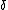 is the boundary-layer thickness and
is the boundary-layer thickness and  is the kinematic viscosity
is the kinematic viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
.
However the semi-infinite plate has no natural length scale
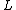 and so the steady, incompressible, two-dimensional boundary-layer equations for continuity and momentum are
and so the steady, incompressible, two-dimensional boundary-layer equations for continuity and momentum areContinuity:
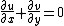
x-Momentum:

(note that the x-independence of
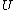 has been accounted for in the boundary-layer
has been accounted for in the boundary-layerBoundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
equations)
admit a similarity solution. In the system of partial differential equations written above it is assumed that a fixed solid body wall is parallel to the x-direction
whereas the y-direction is normal with respect to the fixed wall.
 and
and  denote here the x- and y-components of the fluid velocity vector.
denote here the x- and y-components of the fluid velocity vector.Furthermore, from the scaling argument it is apparent that the boundary layer grows with the downstream coordinate
 , e.g.
, e.g.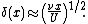
This suggests adopting the similarity variable

and writing
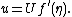
It proves convenient to work with the stream function
Stream function
The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
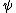 , in which case
, in which case
and on differentiating, to find the velocities, and substituting into the boundary-layer equation we obtain the Blasius equation
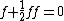
subject to
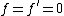 on
on 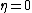 and
and as
as 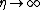 . This non-linear ODE can be solved numerically, with the shooting method
. This non-linear ODE can be solved numerically, with the shooting methodShooting method
In numerical analysis, the shooting method is a method for solving a boundary value problem by reducing it to the solution of an initial value problem...
proving an effective choice.
The shear stress on the plate

can then be computed. The numerical solution gives
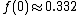 .
.Falkner–Skan boundary layer
We can generalize the Blasius boundary layer by considering a wedge at an angle of attack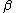 from some uniform velocity field
from some uniform velocity field 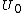 . We then estimate the outer flow to be of the form:
. We then estimate the outer flow to be of the form: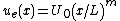
Where
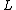 is a characteristic length and m is a dimensionless constant. In the Blasius solution, m = 0 corresponding to an angle of attack of zero radians. Thus we can write:
is a characteristic length and m is a dimensionless constant. In the Blasius solution, m = 0 corresponding to an angle of attack of zero radians. Thus we can write: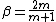
As in the Blasius solution, we use a similarity variable
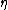 to solve the Navier-Stokes Equations.
to solve the Navier-Stokes Equations.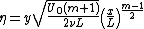
It becomes easier to describe this in terms of its stream function which we write as
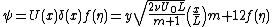
Thus the initial differential equation which was written as follows:
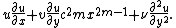
Can now be expressed in terms of the non-linear ODE known as the Falkner–Skan equation (named after V. M. Falkner and Sylvia W. Skan).
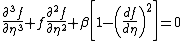
(note that
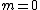 produces the Blasius equation). See Wilcox 2007.
produces the Blasius equation). See Wilcox 2007.In 1937 Douglas Hartree
Douglas Hartree
Douglas Rayner Hartree PhD, FRS was an English mathematician and physicist most famous for the development of numerical analysis and its application to the Hartree-Fock equations of atomic physics and the construction of the meccano differential analyser.-Early life:Douglas Hartree was born in...
revealed that physical solutions exist only in the range
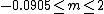 . Here, m<0 corresponds to an adverse pressure gradient (often resulting in boundary layer separation) while m > 0 represents a favorable pressure gradient.
. Here, m<0 corresponds to an adverse pressure gradient (often resulting in boundary layer separation) while m > 0 represents a favorable pressure gradient.

