Borel hierarchy
Encyclopedia
In mathematical logic
, the Borel hierarchy is a stratification of the Borel algebra
generated by the open subsets of a Polish space
; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number
called the rank of the Borel set. The Borel hierarchy is of particular interest in descriptive set theory
.
One common use of the Borel hierarchy is to prove facts about the Borel sets using transfinite induction
on rank. Properties of sets of small finite ranks are important in measure theory and analysis
.
A short proof that the Borel algebra is well defined proceeds by showing that the entire powerset of the space is closed under complements and countable unions, and thus the Borel algebra is the intersection of all families of subsets of the space that have these closure properties. This proof does not give a simple procedure for determining whether a set is Borel. A motivation for the Borel hierarchy is to provide a more explicit characterization of the Borel sets.
, 
, and 
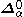for every countable ordinal 
greater than zero. Each of these classes consists of subsets of X. The classes are defined inductively from the following rules:
The motivation for the hierarchy is to follow the way in which a Borel set could be constructed from open sets using complementation and countable unions.
A Borel set is said to have finite rank if it is in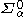
for some finite ordinal α; otherwise it has infinite rank.
The hierarchy can be shown to have the following properties:
and recursion theory
. The lightface Borel hierarchy extends the arithmetical hierarchy
of subsets of an effective Polish space
. It is closely related to the hyperarithmetical hierarchy.
The lightface Borel hierarchy can be defined on any effective Polish space. It consists of classes
, 
and 
for each nonzero countable ordinal 
less than the Church-Kleene ordinal
. Each class consists of subsets of the space. The classes, and codes for elements of the classes, are inductively defined as follows:
A code for a lightface Borel set gives complete information about how to recover the set from sets of smaller rank. This contrasts with the boldface hierarchy, where no such effectivity is required. Each lightface Borel set has infinitely many distinct codes. Other coding systems are possible; the crucial idea is that a code must effectively distinguish between effectively open sets, complements of sets represented by previous codes, and computable enumerations of sequences of codes.
It can be shown that for each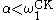
there are sets in 
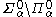, and thus the hierarchy does not collapse. No new sets would be added at stage 
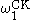, however.
A famous theorem due to Spector and Kleene states that a set is in the lightface Borel hierarchy if and only if it is at level
of the analytical hierarchy
. These sets are also called hyperarithmetic.
The code for a lightface Borel set A can be used to inductively define a tree whose nodes are labeled by codes. The root of the tree is labeled by the code for A. If a node is labeled by a code of the form (1,c) then it has a child node whose code is c. If a node is labeled by a code of the form (2,e) then it has one child for each code enumerated by the program with index e. If a node is labeled with a code of the form (0,e) then it has no children. This tree describes how A is built from sets of smaller rank. The ordinals used in the construction of A ensure that this tree has no infinite path, because any infinite path through the tree would have to include infinitely many codes starting with 2, and thus would give an infinite decreasing sequence of ordinals. Conversely, if an arbitrary subtree of
has its nodes labeled by codes in a consistent way, and the tree has no infinite paths, then the code at the root of the tree is a code for a lightface Borel set. The rank of this set is bounded by the order type of the tree in the Kleene–Brouwer order
. Because the tree is arithmetically definable, this rank must be less than
. This is the origin of the Church-Kleene ordinal in the definition of the lightface hierarchy.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the Borel hierarchy is a stratification of the Borel algebra
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
generated by the open subsets of a Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
called the rank of the Borel set. The Borel hierarchy is of particular interest in descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
.
One common use of the Borel hierarchy is to prove facts about the Borel sets using transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
on rank. Properties of sets of small finite ranks are important in measure theory and analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
Borel sets
The Borel algebra in an arbitrary topological space is the smallest collection of subsets of the space that contains the open sets and is closed under countable unions and complementation. It can be shown that the Borel algebra is closed under countable intersections as well.A short proof that the Borel algebra is well defined proceeds by showing that the entire powerset of the space is closed under complements and countable unions, and thus the Borel algebra is the intersection of all families of subsets of the space that have these closure properties. This proof does not give a simple procedure for determining whether a set is Borel. A motivation for the Borel hierarchy is to provide a more explicit characterization of the Borel sets.
Boldface hierarchy
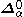The Borel hierarchy or boldface Borel hierarchy on a space X consists of classes, , and for every countable ordinal greater than zero. Each of these classes consists of subsets of X. The classes are defined inductively from the following rules:
- A set is
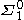if and only if it is open. - A set is
if and only if its complement is 
. - A set
is 
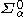for 
if and only if there is a sequence of sets 
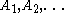such that each 
is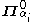 
for some 
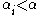and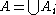 
. - A set is
if and only if it is both 
and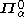 
.
The motivation for the hierarchy is to follow the way in which a Borel set could be constructed from open sets using complementation and countable unions.
A Borel set is said to have finite rank if it is in
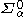for some finite ordinal α; otherwise it has infinite rank.The hierarchy can be shown to have the following properties:
-
. Moreover, a set is in this union if and only if it is Borel. - For every α,
. Thus, once a set is in 
or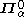 
, that set will be in all classes in the hierarchy corresponding to ordinals greater than α - If
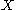is an uncountable Polish space, it can be shown that 
is not contained in 
for any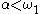 
, and thus the hierarchy does not collapse.
Borel sets of small rank
The classes of small rank are known by alternate names in classical descriptive set theory.- The
sets are the open sets. The 
sets are the closed sets. - The
sets are countable unions of closed sets, and are called Fσ setsF-sigma setIn mathematics, an Fσ set is a countable union of closed sets. The notation originated in France with F for fermé and σ for somme ....
. The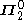
sets are the dual class, and can be written as a countable intersection of open sets. These sets are called Gδ setsG-delta setIn the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
.
Lightface hierarchy
The lightface Borel hierarchy is an effective version of the boldface Borel hierarchy. It is important in effective descriptive set theoryEffective descriptive set theory
Effective descriptive set theory is the branch of descriptive set theory dealing with sets of reals having lightface definitions; that is, definitions that do not require an arbitrary real parameter. Thus effective descriptive set theory combines descriptive set theory with recursion theory....
and recursion theory
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
. The lightface Borel hierarchy extends the arithmetical hierarchy
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
of subsets of an effective Polish space
Effective Polish space
In mathematical logic, an effective Polish space is a complete separable metric space that has a computable presentation. Such spaces are studied in effective descriptive set theory and in constructive analysis.- Definition :...
. It is closely related to the hyperarithmetical hierarchy.
The lightface Borel hierarchy can be defined on any effective Polish space. It consists of classes
, and for each nonzero countable ordinal less than the Church-Kleene ordinalRecursive ordinal
In mathematics, specifically set theory, an ordinal \alpha is said to be recursive if there is a recursive binary relation R that well-orders a subset of the natural numbers and the order type of that ordering is \alpha....
. Each class consists of subsets of the space. The classes, and codes for elements of the classes, are inductively defined as follows:
- A set is
if and only if it is effectively open, that is, an open set which is the union of a computably enumerable sequence of basic open sets. A code for such a set is a pair (0,e), where e is the index of a program enumerating the sequence of basic open sets. - A set is
if and only if its complement is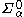 
. A code for one of these sets is a pair (1,c) where c is a code for the complementary set. - A set is
if there is a computably enumerable sequence of codes for a sequence 
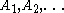of sets such that each 
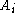is 
for some 
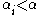and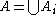 
. A code for a 
set is a pair (2,e), where e is an index of a program enumerating the codes of the sequence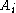 
.
A code for a lightface Borel set gives complete information about how to recover the set from sets of smaller rank. This contrasts with the boldface hierarchy, where no such effectivity is required. Each lightface Borel set has infinitely many distinct codes. Other coding systems are possible; the crucial idea is that a code must effectively distinguish between effectively open sets, complements of sets represented by previous codes, and computable enumerations of sequences of codes.
It can be shown that for each
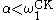there are sets in 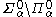, and thus the hierarchy does not collapse. No new sets would be added at stage 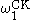, however.A famous theorem due to Spector and Kleene states that a set is in the lightface Borel hierarchy if and only if it is at level
of the analytical hierarchyAnalytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
. These sets are also called hyperarithmetic.
The code for a lightface Borel set A can be used to inductively define a tree whose nodes are labeled by codes. The root of the tree is labeled by the code for A. If a node is labeled by a code of the form (1,c) then it has a child node whose code is c. If a node is labeled by a code of the form (2,e) then it has one child for each code enumerated by the program with index e. If a node is labeled with a code of the form (0,e) then it has no children. This tree describes how A is built from sets of smaller rank. The ordinals used in the construction of A ensure that this tree has no infinite path, because any infinite path through the tree would have to include infinitely many codes starting with 2, and thus would give an infinite decreasing sequence of ordinals. Conversely, if an arbitrary subtree of
has its nodes labeled by codes in a consistent way, and the tree has no infinite paths, then the code at the root of the tree is a code for a lightface Borel set. The rank of this set is bounded by the order type of the tree in the Kleene–Brouwer orderKleene–Brouwer order
In descriptive set theory, the Kleene–Brouwer order is a linear order on finite sequences of some linearly ordered set In descriptive set theory, the Kleene–Brouwer order is a linear order on finite sequences of some linearly ordered set In descriptive set theory, the Kleene–Brouwer order is a...
. Because the tree is arithmetically definable, this rank must be less than
. This is the origin of the Church-Kleene ordinal in the definition of the lightface hierarchy.