
Quartic reciprocity
Encyclopedia
Quartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic
number theory
that state conditions under which the congruence
x4 ≡ p (mod q) is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the congruence x4 ≡ p (mod q) to that of x4 ≡ q (mod p).
made the first conjectures about biquadratic reciprocity. Gauss
published two monographs on biquadratic reciprocity. In the first one (1828) he proved Euler's conjecture about the biquadratic character of 2. In the second one (1832) he stated the biquadratic reciprocity law for the Gaussian integers and proved the supplementary formulas. He said that a third monograph would be forthcoming with the proof of the general theorem, but it never appeared. Jacobi presented proofs in his Königsberg lectures of 1836–37. The first published proofs were by Eisenstein.
Since then a number of other proofs of the classical (Gaussian) version have been found, as well as alternate statements. Lemmermeyer states that there has been an explosion of interest in the rational reciprocity laws since the 1970's.
As is often the case in number theory, it is easiest to work modulo prime numbers, so in this section all moduli p, q, etc., are assumed to positive, odd primes.
, states that −1 is a quadratic nonresidue (mod q), so that for any integer x, one of x and −x is a quadratic residue and the other one is a nonresidue. Thus, if r ≡ a2 (mod q) is a quadratic residue, then if a ≡ b2 is a residue, r ≡ a2 ≡ b4 (mod q) is a biquadratic residue, and if a is a nonresidue, −a is a residue, −a ≡ b2, and again, r ≡ (−a)2 ≡ b4 (mod q) is a biquadratic residue.
Therefore, the only interesting case is when the modulus p ≡ 1 (mod 4).
Gauss proved that if p ≡ 1 (mod 4) then the nonzero residue classes (mod p) can be divided into four sets, each containing (p−1)/4 numbers. Let e be a quadratic nonresidue. The first set is the quartic residues; the second one is e times the numbers in the first set, the third is e2 times the numbers in the first set, and the fourth one is e3 times the numbers in the first set. Another way to describe this division is to let g be a primitive root
(mod p); then the first set is all the numbers whose indices with respect to this root are ≡ 0 (mod 4), the second set is all those whose indices are ≡ 1 (mod 4), etc. In the vocabulary of group theory
, the first set is a subgroup of index
4 (of the multiplicative group Z/pZ×), and the other three are its cosets.
The first set is the biquadratic residues, the third set is the quadratic residues that are not quartic residues, and the second and fourth sets are the quadratic nonresidues. Gauss proved that −1 is a biquadratic residue if p ≡ 1 (mod 8) and a quadratic, but not biquadratic, residue, when p ≡ 5 (mod 8).
2 is a quadratic residue mod p if and only if p ≡ ±1 (mod 8). Since p is also ≡ 1 (mod 4), this means p ≡ 1 (mod 8). Every such prime is the sum of a square and twice a square.
Gauss proved
Let q = a2 + 2b2 ≡ 1 (mod 8) be a prime number. Then
Every prime p ≡ 1 (mod 4) is the sum of two squares. If p = a2 + b2 where a is odd and b is even, Gauss proved that
2 belongs to the first (respectively second, third, or fourth) class defined above if and only if b ≡ 0 (resp. 2, 4, or 6) (mod 8). The first case of this is one of Euler's conjectures:
states that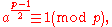 so if p ≡ 1 (mod 4),
so if p ≡ 1 (mod 4), 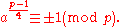
Define the rational quartic residue symbol for prime p ≡ 1 (mod 4) and quadratic residue a (mod p) as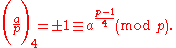 It is easy to prove that a is a biquadratic residue (mod p) if and only if
It is easy to prove that a is a biquadratic residue (mod p) if and only if 
Dirichlet simplified Gauss's proof of the biquadratic character of 2 (his proof only requires quadratic reciprocity for the integers) and put the result in the following form:
Let p = a2 + b2 ≡ 1 (mod 4) be prime, and let i ≡ b/a (mod p). Then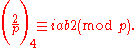 (Note that i2 ≡ −1 (mod p).)
(Note that i2 ≡ −1 (mod p).)
In fact, let p = a2 + b2 = c2 + 2d2 = e2 − 2f2 ≡ 1 (mod 8) be prime, and assume a is odd. Then where
where  is the ordinary Legendre symbol
is the ordinary Legendre symbol
.
Going beyond the character of 2, let the prime p = a2 + b2 where b is even, and let q be a prime such that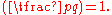 Quadratic reciprocity says that
Quadratic reciprocity says that  where
where 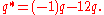 Let σ2 ≡ p (mod q). Then
Let σ2 ≡ p (mod q). Then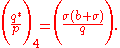 This implies that
This implies that

The first few examples are: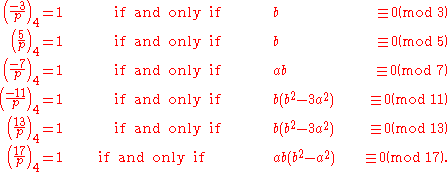
Euler had conjectured the rules for 2, −3 and 5, but did not prove any of them.
Dirichlet also proved that if p ≡ 1 (mod 4) is prime and then
then
This has been extended from 17 to 17, 73, 97, and 193 by Brown and Lehmer.
They all assume that p = a2 + b2 and q = c2 + d2 are primes where b and d are even, and that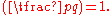
Gosset's version is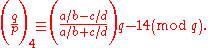
Letting i2 ≡ −1 (mod p) and j2 ≡ −1 (mod q), Frölich's law is
Burde stated his in the form:
Note that
 . Then e2 = p f2 + q g2 has non-trivial integer solutions, and
. Then e2 = p f2 + q g2 has non-trivial integer solutions, and
Let p ≡ q ≡ 1 (mod 4) be primes and assume p = r2 + q s2. Then
Let p = 1 + 4x2 be prime, let a be any odd number that divides x, and let Then a* is a biquadratic residue (mod p).
Then a* is a biquadratic residue (mod p).
Let p = a2 + 4b2 = c2 + 2d2 ≡ 1 (mod 8) be prime. Then all the divisors of c4 − p a2 are biquadratic residues (mod p). The same is true for all the divisors of d4 − p b2.
These numbers are now called the ring
of Gaussian integers, denoted by Z[i]. Note that i is a fourth root of 1.
In a footnote he adds
The numbers built up from a cube root of unity are now called the ring of Eisenstein integers. The "other imaginary quantities" needed for the "theory of residues of higher powers" are the rings of integers
of the cyclotomic number field
s; the Gaussian and Eisenstein integers are the simplest examples of these.
The units are the numbers that divide 1. They are 1, i, −1, and −i. They are similar to 1 and −1 in the ordinary integers, in that they divide every number. The units are the powers of i.
Given a number λ = a + bi, its conjugate is a − bi and its associates are the four numbers
The norm of λ = a + bi is the number Nλ = a2 + b2. If λ and μ are two Gaussian integers, Nλμ = Nλ Nμ; in other words, the norm is multiplicative. The norm of zero is zero, the norm of any other number is a positive integer. ε is a unit if and only if Nε = 1.
Gauss proves that Z[i] is a unique factorization domain
and shows that the primes fall into three classes:
Thus, inert primes are 3, 7, 11, 19, ... and a factorization of the split primes is
The associates and conjugate of a prime are also primes.
Note that the norm of an inert prime q is Nq = q2 ≡ 1 (mod 4); thus the norm of all primes other than 1 + i and its associates is ≡ 1 (mod 4).
Gauss calls a number in Z[i] odd if its norm is an odd integer. Thus all primes except 1 + i and its associates are odd. The product of two odd numbers is odd and the conjugate and associates of an odd number are odd.
In order to state the unique factorization theorem, it is necessary to have a way of distinguishing one of the associates of a number. Gauss defines an odd number to be primary if it is ≡ 1 (mod (1 + i)3). It is straightforward to show that every odd number has exactly one primary associate. An odd number λ = a + bi is primary if a + b ≡ a − b ≡ 1 (mod 4); i.e., a ≡ 1 and b ≡ 0, or a ≡ 3 and b ≡ 2 (mod 4). The product of two primary numbers is primary and the conjugate of a primary number is also primary.
The unique factorization theorem for Z[i] is: if λ ≠ 0, then
where 0 ≤ μ ≤ 3, ν ≥ 0, the πis are primary primes and the αis ≥ 1, and this representation is unique, up to the order of the factors.
The notions of congruence
and greatest common divisor
are defined the same way in Z[i] as they are for the ordinary integers Z. Because the units divide all numbers, a congruence (mod λ) is also true modulo any associate of λ, and any associate of a GCD is also a GCD.
: if α is not divisible by an odd prime π, then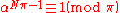
Since Nπ ≡ 1 (mod 4),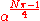 makes sense, and
makes sense, and 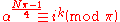 for a unique unit ik.
for a unique unit ik.
This unit is called the quartic or biquadratic residue character of α (mod π) and is denoted by
It has formal properties similar to those of the Legendre symbol
.
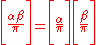
 where the bar denotes complex conjugation.
where the bar denotes complex conjugation.
The biquadratic character can be extended to odd composite numbers in the "denominator" in the same way the Legendre symbol is generalized into the Jacobi symbol
. As in that case, if the "denominator" is composite, the symbol can equal one without the conguence being solvable: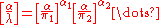 where
where 
Let π and θ be distinct primary primes of Z[i]. Then
Just as the quadratic reciprocity law for the Legendre symbol is also true for the Jacobi symbol, the requirement that the numbers be prime is not needed; it suffices that they be odd relatively prime nonunits. Probably the most well-known statement is:
Let π and θ be primary relatively prime nonunits. Then
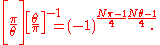
There are supplementary theorems for the units and the half-even prime 1 + i.
if π = a + bi is a primary prime, then
and thus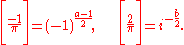
Also, if π = a + bi is a primary prime, and b ≠ 0 then
 (if b = 0 the symbol is 0).
(if b = 0 the symbol is 0).
Jacobi defined π = a + bi to be primary if a ≡ 1 (mod 4). With this normalization, the law takes the form
Let α = a + bi and β = c + di where a ≡ c ≡ 1 (mod 4) and b and d are even be relatively prime nonunits. Then

The following version was found in Gauss's unpublished manuscripts.
Let α = a + 2bi and β = c + 2di where a and c are odd be relatively prime nonunits. Then
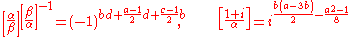
The law can be stated without using the concept of primary:
If λ is odd, let ε(λ) be the unique unit congruent to λ (mod (1 + i)3); i.e., ε(λ) = ik ≡ λ (mod 2 + 2i), where 0 ≤ k ≤ 3. Then for odd and relatively prime α and β, neither one a unit,
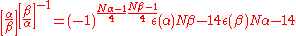
For odd λ, let Then if λ and μ are relatively prime nonunits, Eisenstein proved
Then if λ and μ are relatively prime nonunits, Eisenstein proved

These are in Gauss's Werke, Vol II, pp. 65–92 and 93–148
German translations are in pp. 511–533 and 534–586 of the following, which also has the Disquisitiones Arithmeticae
and Gauss's other papers on number theory.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
that state conditions under which the congruence
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
x4 ≡ p (mod q) is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the congruence x4 ≡ p (mod q) to that of x4 ≡ q (mod p).
History
EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
made the first conjectures about biquadratic reciprocity. Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
published two monographs on biquadratic reciprocity. In the first one (1828) he proved Euler's conjecture about the biquadratic character of 2. In the second one (1832) he stated the biquadratic reciprocity law for the Gaussian integers and proved the supplementary formulas. He said that a third monograph would be forthcoming with the proof of the general theorem, but it never appeared. Jacobi presented proofs in his Königsberg lectures of 1836–37. The first published proofs were by Eisenstein.
Since then a number of other proofs of the classical (Gaussian) version have been found, as well as alternate statements. Lemmermeyer states that there has been an explosion of interest in the rational reciprocity laws since the 1970's.
Integers
A quartic or biquadratic residue (mod p) is any number congruent to the fourth power of an integer (mod p). If x4 ≡ a (mod p) does not have an integer solution, a is a quartic or biquadratic nonresidue (mod p).As is often the case in number theory, it is easiest to work modulo prime numbers, so in this section all moduli p, q, etc., are assumed to positive, odd primes.
Gauss
The first thing to notice when working within the ring Z of integers is that if the prime number q is ≡ 3 (mod 4) then every quadratic residue (mod q) is also a biquadratic residue (mod q). The first supplement of quadratic reciprocityQuadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
, states that −1 is a quadratic nonresidue (mod q), so that for any integer x, one of x and −x is a quadratic residue and the other one is a nonresidue. Thus, if r ≡ a2 (mod q) is a quadratic residue, then if a ≡ b2 is a residue, r ≡ a2 ≡ b4 (mod q) is a biquadratic residue, and if a is a nonresidue, −a is a residue, −a ≡ b2, and again, r ≡ (−a)2 ≡ b4 (mod q) is a biquadratic residue.
Therefore, the only interesting case is when the modulus p ≡ 1 (mod 4).
Gauss proved that if p ≡ 1 (mod 4) then the nonzero residue classes (mod p) can be divided into four sets, each containing (p−1)/4 numbers. Let e be a quadratic nonresidue. The first set is the quartic residues; the second one is e times the numbers in the first set, the third is e2 times the numbers in the first set, and the fourth one is e3 times the numbers in the first set. Another way to describe this division is to let g be a primitive root
Primitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
(mod p); then the first set is all the numbers whose indices with respect to this root are ≡ 0 (mod 4), the second set is all those whose indices are ≡ 1 (mod 4), etc. In the vocabulary of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the first set is a subgroup of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
4 (of the multiplicative group Z/pZ×), and the other three are its cosets.
The first set is the biquadratic residues, the third set is the quadratic residues that are not quartic residues, and the second and fourth sets are the quadratic nonresidues. Gauss proved that −1 is a biquadratic residue if p ≡ 1 (mod 8) and a quadratic, but not biquadratic, residue, when p ≡ 5 (mod 8).
2 is a quadratic residue mod p if and only if p ≡ ±1 (mod 8). Since p is also ≡ 1 (mod 4), this means p ≡ 1 (mod 8). Every such prime is the sum of a square and twice a square.
Gauss proved
Let q = a2 + 2b2 ≡ 1 (mod 8) be a prime number. Then
- 2 is a biquadratic residue (mod q) if and only if a ≡ ±1 (mod 8), and
- 2 is a quadratic, but not a biquadratic, residue (mod q) if and only if a ≡ ±3 (mod 8).
Every prime p ≡ 1 (mod 4) is the sum of two squares. If p = a2 + b2 where a is odd and b is even, Gauss proved that
2 belongs to the first (respectively second, third, or fourth) class defined above if and only if b ≡ 0 (resp. 2, 4, or 6) (mod 8). The first case of this is one of Euler's conjectures:
- 2 is a biquadratic residue of a prime p ≡ 1 (mod 4) if and only if p = a2 + 64b2.
Dirichlet
For an odd prime number p and a quadratic residue a (mod p), Euler's criterionEuler's criterion
In mathematics, Euler's criterion is used in determining in number theory whether a given integer is a quadratic residue modulo a prime.-Definition:Euler's criterion states:Let p be an odd prime and a an integer coprime to p. Then...
states that
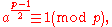 so if p ≡ 1 (mod 4),
so if p ≡ 1 (mod 4), 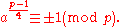
Define the rational quartic residue symbol for prime p ≡ 1 (mod 4) and quadratic residue a (mod p) as
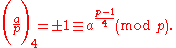 It is easy to prove that a is a biquadratic residue (mod p) if and only if
It is easy to prove that a is a biquadratic residue (mod p) if and only if 
Dirichlet simplified Gauss's proof of the biquadratic character of 2 (his proof only requires quadratic reciprocity for the integers) and put the result in the following form:
Let p = a2 + b2 ≡ 1 (mod 4) be prime, and let i ≡ b/a (mod p). Then
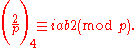 (Note that i2 ≡ −1 (mod p).)
(Note that i2 ≡ −1 (mod p).)In fact, let p = a2 + b2 = c2 + 2d2 = e2 − 2f2 ≡ 1 (mod 8) be prime, and assume a is odd. Then
 where
where  is the ordinary Legendre symbol
is the ordinary Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
.
Going beyond the character of 2, let the prime p = a2 + b2 where b is even, and let q be a prime such that
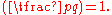 Quadratic reciprocity says that
Quadratic reciprocity says that  where
where 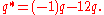 Let σ2 ≡ p (mod q). Then
Let σ2 ≡ p (mod q). Then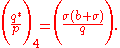 This implies that
This implies that
The first few examples are:
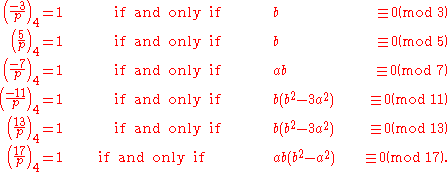
Euler had conjectured the rules for 2, −3 and 5, but did not prove any of them.
Dirichlet also proved that if p ≡ 1 (mod 4) is prime and
 then
then
This has been extended from 17 to 17, 73, 97, and 193 by Brown and Lehmer.
Burde
There are a number of equivalent ways of stating Burde's rational biquadratic reciprocity law.They all assume that p = a2 + b2 and q = c2 + d2 are primes where b and d are even, and that
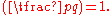
Gosset's version is
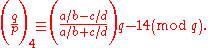
Letting i2 ≡ −1 (mod p) and j2 ≡ −1 (mod q), Frölich's law is

Burde stated his in the form:

Note that

Miscellany
Let p ≡ q ≡ 1 (mod 4) be primes and assume . Then e2 = p f2 + q g2 has non-trivial integer solutions, and
. Then e2 = p f2 + q g2 has non-trivial integer solutions, and
Let p ≡ q ≡ 1 (mod 4) be primes and assume p = r2 + q s2. Then

Let p = 1 + 4x2 be prime, let a be any odd number that divides x, and let
 Then a* is a biquadratic residue (mod p).
Then a* is a biquadratic residue (mod p).Let p = a2 + 4b2 = c2 + 2d2 ≡ 1 (mod 8) be prime. Then all the divisors of c4 − p a2 are biquadratic residues (mod p). The same is true for all the divisors of d4 − p b2.
Background
In his second monograph on biquadratic reciprocity Gauss displays some examples and makes conjectures that imply the theorems listed above for the biquadratic character of small primes. He makes some general remarks, and admits there is no obvious general rule at work. He goes on to sayThe theorems on biquadratic residues gleam with the greatest simplilcity and genuine beauty only when the field of arithmetic is extended to imaginary numbers, so that without restriction, the numbers of the form a + bi constitute the object of study ... we call such numbers integral complex numbers. [bold in the original]
These numbers are now called the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of Gaussian integers, denoted by Z[i]. Note that i is a fourth root of 1.
In a footnote he adds
The theory of cubic residues must be based in a similar way on a consideration of numbers of the form a + bh where h is an imaginary root of the equation h3 = 1 ... and similarly the theory of residues of higher powers leads to the introduction of other imaginary quantities.
The numbers built up from a cube root of unity are now called the ring of Eisenstein integers. The "other imaginary quantities" needed for the "theory of residues of higher powers" are the rings of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of the cyclotomic number field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
s; the Gaussian and Eisenstein integers are the simplest examples of these.
Facts and terminology
Gauss develops the arithmetic theory of the "integral complex numbers" and shows that it is quite similar to the arithmetic of ordinary integers. This is where the terms unit, associate, norm, and primary were introduced into mathematics.The units are the numbers that divide 1. They are 1, i, −1, and −i. They are similar to 1 and −1 in the ordinary integers, in that they divide every number. The units are the powers of i.
Given a number λ = a + bi, its conjugate is a − bi and its associates are the four numbers
- λ = +a + bi
- iλ = −b + ai
- −λ = −a − bi
- −iλ = +b − ai
The norm of λ = a + bi is the number Nλ = a2 + b2. If λ and μ are two Gaussian integers, Nλμ = Nλ Nμ; in other words, the norm is multiplicative. The norm of zero is zero, the norm of any other number is a positive integer. ε is a unit if and only if Nε = 1.
Gauss proves that Z[i] is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
and shows that the primes fall into three classes:
- 2 is a special case: 2 = i3 (1 + i)2. It is the only prime in Z divisible by the square of a prime in Z[i]. In algebraic number theory, 2 is said to ramify in Z[i].
- Positive primes in Z ≡ 3 (mod 4) are also primes in Z[i]. In algebraic number theory, these primes are said to remain inert in Z[i].
- Positive primes in Z ≡ 1 (mod 4) are the product of two conjugate primes in Z[i]. In algebraic number theory, these primes are said to split in Z[i].
Thus, inert primes are 3, 7, 11, 19, ... and a factorization of the split primes is
- 5 = (2 + i) × (2 − i),
- 13 = (2 + 3i) × (2 − 3i),
- 17 = (4 + i) × (4 − i),
- 29 = (2 + 5i) × (2 − 5i), ...
The associates and conjugate of a prime are also primes.
Note that the norm of an inert prime q is Nq = q2 ≡ 1 (mod 4); thus the norm of all primes other than 1 + i and its associates is ≡ 1 (mod 4).
Gauss calls a number in Z[i] odd if its norm is an odd integer. Thus all primes except 1 + i and its associates are odd. The product of two odd numbers is odd and the conjugate and associates of an odd number are odd.
In order to state the unique factorization theorem, it is necessary to have a way of distinguishing one of the associates of a number. Gauss defines an odd number to be primary if it is ≡ 1 (mod (1 + i)3). It is straightforward to show that every odd number has exactly one primary associate. An odd number λ = a + bi is primary if a + b ≡ a − b ≡ 1 (mod 4); i.e., a ≡ 1 and b ≡ 0, or a ≡ 3 and b ≡ 2 (mod 4). The product of two primary numbers is primary and the conjugate of a primary number is also primary.
The unique factorization theorem for Z[i] is: if λ ≠ 0, then

where 0 ≤ μ ≤ 3, ν ≥ 0, the πis are primary primes and the αis ≥ 1, and this representation is unique, up to the order of the factors.
The notions of congruence
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
and greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
are defined the same way in Z[i] as they are for the ordinary integers Z. Because the units divide all numbers, a congruence (mod λ) is also true modulo any associate of λ, and any associate of a GCD is also a GCD.
Quartic residue character
Gauss proves the analogue of Fermat's theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
: if α is not divisible by an odd prime π, then
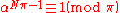
Since Nπ ≡ 1 (mod 4),
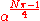 makes sense, and
makes sense, and 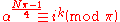 for a unique unit ik.
for a unique unit ik.This unit is called the quartic or biquadratic residue character of α (mod π) and is denoted by

It has formal properties similar to those of the Legendre symbol
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
.
- The congruence
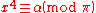 is solvable in Z[i] if and only if
is solvable in Z[i] if and only if 

 where the bar denotes complex conjugation.
where the bar denotes complex conjugation.- if π and θ are associates,

- if α ≡ β (mod π),
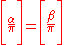
The biquadratic character can be extended to odd composite numbers in the "denominator" in the same way the Legendre symbol is generalized into the Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
. As in that case, if the "denominator" is composite, the symbol can equal one without the conguence being solvable:
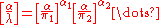 where
where 
- If a and b are ordinary integers, a ≠ 0, |b| > 1, gcd(a, b) = 1, then
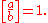
Statements of the theorem
Gauss stated the law of biquadratic reciprocity in this form:Let π and θ be distinct primary primes of Z[i]. Then
- if either π or θ or both are ≡ 1 (mod 4), then
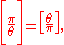 but
but
- if both π and θ are ≡ 3 + 2i (mod 4), then
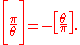
Just as the quadratic reciprocity law for the Legendre symbol is also true for the Jacobi symbol, the requirement that the numbers be prime is not needed; it suffices that they be odd relatively prime nonunits. Probably the most well-known statement is:
Let π and θ be primary relatively prime nonunits. Then
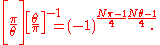
There are supplementary theorems for the units and the half-even prime 1 + i.
if π = a + bi is a primary prime, then

and thus
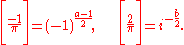
Also, if π = a + bi is a primary prime, and b ≠ 0 then
 (if b = 0 the symbol is 0).
(if b = 0 the symbol is 0).Jacobi defined π = a + bi to be primary if a ≡ 1 (mod 4). With this normalization, the law takes the form
Let α = a + bi and β = c + di where a ≡ c ≡ 1 (mod 4) and b and d are even be relatively prime nonunits. Then

The following version was found in Gauss's unpublished manuscripts.
Let α = a + 2bi and β = c + 2di where a and c are odd be relatively prime nonunits. Then
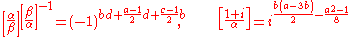
The law can be stated without using the concept of primary:
If λ is odd, let ε(λ) be the unique unit congruent to λ (mod (1 + i)3); i.e., ε(λ) = ik ≡ λ (mod 2 + 2i), where 0 ≤ k ≤ 3. Then for odd and relatively prime α and β, neither one a unit,
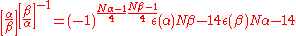
For odd λ, let
 Then if λ and μ are relatively prime nonunits, Eisenstein proved
Then if λ and μ are relatively prime nonunits, Eisenstein proved
Literature
The references to the original papers of Euler, Dirichlet, and Eisenstein were copied from the bibliographies in Lemmermeyer and Cox, and were not used in the preparation of this article.Euler
This was actually written 1748–1750, but was only published posthumously; It is in Vol V, pp. 182–283 ofGauss
The two monographs Gauss published on biquadratic reciprocity have consecutively-numbered sections: the first contains §§ 1–23 and the second §§ 24–76. Footnotes referencing these are of the form "Gauss, BQ, § n". Footnotes referencing the Disquisitiones Arithmeticae are of the form "Gauss, DA, Art. n".These are in Gauss's Werke, Vol II, pp. 65–92 and 93–148
German translations are in pp. 511–533 and 534–586 of the following, which also has the Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
and Gauss's other papers on number theory.

