Seifert surface
Encyclopedia
In mathematics
, a Seifert surface (named after German
mathematician
Herbert Seifert
) is a surface
whose boundary is a given knot
or link
.
Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface. Seifert surfaces are also interesting in their own right, and the subject of considerable research.
Specifically, let L be a tame oriented knot or link in Euclidean 3-space
(or in the 3-sphere
). A Seifert surface is a compact
, connected
, oriented surface
S embedded in 3-space whose boundary is L such that the orientation on L is just the induced orientation from S, and every connected component of S has non-empty boundary.
Note that any compact, connected, oriented surface with nonempty boundary in Euclidean 3-space is the Seifert surface associated to its boundary link. A single knot or link can have many different inequivalent Seifert surfaces. A Seifert surface must be oriented. It is possible to associate unoriented (and not necessarily orientable) surfaces to knots as well.
The standard Möbius strip
has the unknot
for a boundary but is not considered to be a Seifert surface for the unknot because it is not orientable.
The "checkerboard" coloring of the usual minimal crossing projection of the trefoil knot
gives a Mobius strip with three half twists. As with the previous example, this is not a Seifert surface as it is not orientable. Applying Seifert's algorithm to this diagram, as expected, does produce a Seifert surface; in this case, it is a punctured torus of genus g=1, and the Seifert matrix is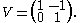
that any link always has an associated Seifert surface. This theorem was first published by Frankl and Pontrjagin in 1930. A different proof was published in 1934 by Herbert Seifert
and relies on what is now called the Seifert algorithm. The algorithm
produces a Seifert surface
, given a projection of the knot or link in question.
Suppose that link has m components (m=1 for a knot), the diagram has d crossing points, and resolving the crossings (preserving the orientation of the knot) yields f circles. Then the surface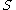
is constructed from f disjoint disks by attaching d bands. The homology group 
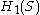is free abelian on 2g generators, where
is the genus
of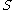
. The intersection form
Q on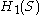
is skew-symmetric, and there is a basis of 2g cycles
with
the direct sum of g copies of
.
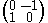The 2g
2g integer Seifert matrix
the linking number
in Euclidean 3-space (or in the 3-sphere
) of ai and the pushoff of aj out of the surface, with
*
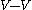where V*=(v(j,i)) the transpose matrix. Every integer 2g
2g matrix 
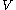with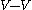 
*
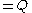arises as the Seifert matrix of a knot with genus g Seifert surface.
The Alexander polynomial
is computed from the Seifert matrix by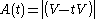
*), which is a polynomial in the indeterminate 
of degree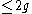 
. The Alexander polynomial is independent of the choice of Seifert surface 
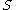, and is an invariant of the knot or link.
The signature of a knot
is the signature of the symmetric Seifert matrix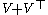
. It is again an invariant of the knot or link.
, to be replaced by a Seifert surface S of genus g+1 and Seifert matrix
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Seifert surface (named after German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Herbert Seifert
Herbert Seifert
Herbert Karl Johannes Seifert was a German mathematician known for his work in topology....
) is a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
whose boundary is a given knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
or link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
.
Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface. Seifert surfaces are also interesting in their own right, and the subject of considerable research.
Specifically, let L be a tame oriented knot or link in Euclidean 3-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(or in the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
). A Seifert surface is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, oriented surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
S embedded in 3-space whose boundary is L such that the orientation on L is just the induced orientation from S, and every connected component of S has non-empty boundary.
Note that any compact, connected, oriented surface with nonempty boundary in Euclidean 3-space is the Seifert surface associated to its boundary link. A single knot or link can have many different inequivalent Seifert surfaces. A Seifert surface must be oriented. It is possible to associate unoriented (and not necessarily orientable) surfaces to knots as well.
Examples
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
has the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
for a boundary but is not considered to be a Seifert surface for the unknot because it is not orientable.
The "checkerboard" coloring of the usual minimal crossing projection of the trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
gives a Mobius strip with three half twists. As with the previous example, this is not a Seifert surface as it is not orientable. Applying Seifert's algorithm to this diagram, as expected, does produce a Seifert surface; in this case, it is a punctured torus of genus g=1, and the Seifert matrix is
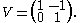
Existence and Seifert matrix
It is a theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
that any link always has an associated Seifert surface. This theorem was first published by Frankl and Pontrjagin in 1930. A different proof was published in 1934 by Herbert Seifert
Herbert Seifert
Herbert Karl Johannes Seifert was a German mathematician known for his work in topology....
and relies on what is now called the Seifert algorithm. The algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
produces a Seifert surface
, given a projection of the knot or link in question.Suppose that link has m components (m=1 for a knot), the diagram has d crossing points, and resolving the crossings (preserving the orientation of the knot) yields f circles. Then the surface
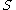is constructed from f disjoint disks by attaching d bands. The homology group 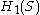is free abelian on 2g generators, where- g = (2 + d − f − m)/2
is the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
of
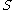. The intersection formIntersection form
Intersection form may refer to:*Intersection theory *intersection form...
Q on
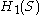is skew-symmetric, and there is a basis of 2g cycles- a1,a2,...,a2g
with
- Q=(Q(ai,aj))
the direct sum of g copies of
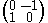.The 2g
2g integer Seifert matrix- V=(v(i,j)) has
the linking numberLinking number
In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other...
in Euclidean 3-space (or in the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
) of ai and the pushoff of aj out of the surface, with
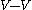*where V*=(v(j,i)) the transpose matrix. Every integer 2g
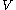2g matrix with 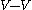* 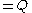arises as the Seifert matrix of a knot with genus g Seifert surface.The Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
is computed from the Seifert matrix by
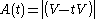*), which is a polynomial in the indeterminate of degree 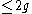. The Alexander polynomial is independent of the choice of Seifert surface 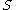, and is an invariant of the knot or link.The signature of a knot
Signature of a knot
The signature of a knot is a topological invariant in knot theory. It may be computed from the Seifert surface.Given a knot K in the 3-sphere, it has a Seifert surface S whose boundary is K...
is the signature of the symmetric Seifert matrix
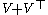. It is again an invariant of the knot or link.Genus of a knot
Seifert surfaces are not at all unique: a Seifert surface S of genus g and Seifert matrix V can be modified by a surgerySurgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
, to be replaced by a Seifert surface S of genus g+1 and Seifert matrix
- V'=V
.
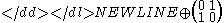The genus of a knot K is the knot invariantKnot invariantIn the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
defined by the minimal genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
g of a Seifert surface for K.
For instance:- An unknotUnknotThe unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
—which is, by definition, the boundary of a discDisk (mathematics)In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
—has genus zero. Moreover, the unknot is the only knot with genus zero. - The trefoil knotTrefoil knotIn topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
has genus one, as does the figure-eight knotFigure-eight knot (mathematics)In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
. - The genus of a (p,q)-torus knotTorus knotIn knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
is (p − 1)(q − 1)/2 - The degree of the Alexander polynomialAlexander polynomialIn mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
is a lower bound on twice the genus of the knot.
A fundamental property of the genus is that it is additive with respect to the knot sum: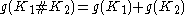
External links
- The SeifertView programme of Jack van WijkJack van WijkJarke J. van Wijk is a Dutch computer scientist, a professor in the Department of Mathematics and Computer Science at the Eindhoven University of Technology, and an expert in information visualization.-Biography:...
visualizes the Seifert surfaces of knots constructed using Seifert's algorithm.
- An unknot