
Étale fundamental group
Encyclopedia
The étale fundamental group is an analogue in algebraic geometry
, for schemes
, of the usual fundamental group
of topological spaces.
, the fundamental group

of a path connected
topological space X is defined to be the group
of loops based at a point modulo homotopy
. When one wants to obtain something similar in the algebraic
category
, this definition encounters problems.
One cannot simply attempt to use the same definition, since the notion of a path does not make sense in general if one is working in positive characteristic
. More to the point, the topology on a scheme
fails to capture much of the structure of the scheme. Simply choosing the "loop" to be an algebraic curve
is not appropriate either, since in the most familiar case (over the complex number
s) such a "loop" has two real
dimension
s rather than one.
In the classification of covering spaces, it is shown that the fundamental group is exactly the group of deck transformations of the universal covering space. This is more promising: finite étale morphism
s are the appropriate generalization of covering spaces
. Unfortunately, the universal covering space is often an infinite covering of the original space, which is unlikely to yield anything manageable in the algebraic category. Finite coverings, on the other hand are tractable, so one can define the algebraic fundamental group as an inverse limit
of automorphism
groups.
Let be a scheme, let
be a scheme, let  be a geometric point of
be a geometric point of 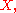 and let
and let  be the category of pairs
be the category of pairs 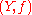 such that
such that 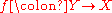 is a finite étale morphism ("finite étale schemes over
is a finite étale morphism ("finite étale schemes over  "). Morphisms
"). Morphisms 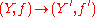 in this category are morphisms
in this category are morphisms  as schemes over
as schemes over  This category has a natural functor given
This category has a natural functor given  , namely the functor
, namely the functor

geometrically this is the fiber of over
over 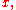 and abstractly it is the covariant Yoneda functor "co-represented" by
and abstractly it is the covariant Yoneda functor "co-represented" by  The quotation marks are because
The quotation marks are because  is not in fact a finite étale morphism, so that
is not in fact a finite étale morphism, so that  is not actually representable (in general). However, it is pro-representable, in fact by "Galois covers" of
is not actually representable (in general). However, it is pro-representable, in fact by "Galois covers" of 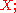 this means that we have a projective system
this means that we have a projective system 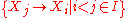 indexed by a directed set
indexed by a directed set
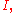 where the
where the  are of course finite étale schemes over
are of course finite étale schemes over 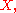
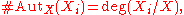 and
and .
.
Note that for two such the map
the map  induces a group homomorphism
induces a group homomorphism

which produces a projective system of automorphism groups from the projective system . We then make the following definition: the étale fundamental group
. We then make the following definition: the étale fundamental group 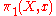 of
of  at
at  is the inverse limit
is the inverse limit
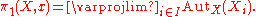
k. Essentially by definition, the fundamental group of k can be shown to be isomorphic to the absolute Galois group
Gal (ksep / k). More precisely, the choice of a geometric point of Spec (k) is equivalent to giving a separably closed extension field K, and the fundamental group with respect to that base point identifies with the Galois group Gal (K / k). This interpretation of the Galois group is known as Grothendieck's Galois theory
.
More generally, for any geometrically connected variety X over a field k (i.e., X is such that Xsep := X ×k ksep is connected) there is an exact sequence
of profinite groups
attached to X. The algebraic fundamental group, as it is typically called in this case, is the profinite completion of π1(X). This is a consequence of the Riemann existence theorem, which says that all finite etale coverings of X(C) stem from ones of X. In particular, as the fundamental group of smooth curves over C (i.e., open Riemann surfaces) is well-understood, this determines the algebraic fundamental group. More generally, the fundamental group of a proper scheme over any algebraically closed field of characteristic zero is known, because an extension of algebraically closed fields induces isomorphic fundamental groups.
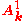 is not topologically finitely generated. The tame fundamental group of some scheme U is a quotient of the usual fundamental group of U which takes into account only covers that are tamely ramified along D, where X is some compactification and D is the complement of U in X. For example, the tame fundamental group of the affine line is zero.
is not topologically finitely generated. The tame fundamental group of some scheme U is a quotient of the usual fundamental group of U which takes into account only covers that are tamely ramified along D, where X is some compactification and D is the complement of U in X. For example, the tame fundamental group of the affine line is zero.
point of view, the fundamental group is a functor
The inverse Galois problem
asks what groups can arise as fundamental groups (or Galois groups of field extensions). Anabelian geometry
, for example Grothendieck's section conjecture, seeks to identify classes of varieties which are determined by their fundamental groups.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, for schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
, of the usual fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of topological spaces.
Topological analogue
In algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the fundamental group

of a path connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
topological space X is defined to be the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of loops based at a point modulo homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
. When one wants to obtain something similar in the algebraic
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, this definition encounters problems.
One cannot simply attempt to use the same definition, since the notion of a path does not make sense in general if one is working in positive characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
. More to the point, the topology on a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
fails to capture much of the structure of the scheme. Simply choosing the "loop" to be an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
is not appropriate either, since in the most familiar case (over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s) such a "loop" has two real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s rather than one.
Covering spaces
This discussion follows Milne.In the classification of covering spaces, it is shown that the fundamental group is exactly the group of deck transformations of the universal covering space. This is more promising: finite étale morphism
Étale morphism
In algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
s are the appropriate generalization of covering spaces
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
. Unfortunately, the universal covering space is often an infinite covering of the original space, which is unlikely to yield anything manageable in the algebraic category. Finite coverings, on the other hand are tractable, so one can define the algebraic fundamental group as an inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
groups.
Let
 be a scheme, let
be a scheme, let  be a geometric point of
be a geometric point of 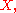 and let
and let  be the category of pairs
be the category of pairs 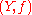 such that
such that 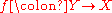 is a finite étale morphism ("finite étale schemes over
is a finite étale morphism ("finite étale schemes over  "). Morphisms
"). Morphisms 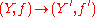 in this category are morphisms
in this category are morphisms  as schemes over
as schemes over  This category has a natural functor given
This category has a natural functor given  , namely the functor
, namely the functor
geometrically this is the fiber of
 over
over 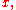 and abstractly it is the covariant Yoneda functor "co-represented" by
and abstractly it is the covariant Yoneda functor "co-represented" by  The quotation marks are because
The quotation marks are because  is not in fact a finite étale morphism, so that
is not in fact a finite étale morphism, so that  is not actually representable (in general). However, it is pro-representable, in fact by "Galois covers" of
is not actually representable (in general). However, it is pro-representable, in fact by "Galois covers" of 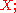 this means that we have a projective system
this means that we have a projective system 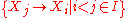 indexed by a directed set
indexed by a directed setDirected set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
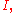 where the
where the  are of course finite étale schemes over
are of course finite étale schemes over 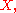
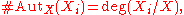 and
and .
.Note that for two such
 the map
the map  induces a group homomorphism
induces a group homomorphism
which produces a projective system of automorphism groups from the projective system
 . We then make the following definition: the étale fundamental group
. We then make the following definition: the étale fundamental group 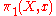 of
of  at
at  is the inverse limit
is the inverse limit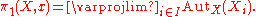
Examples and theorems
The most basic example of a fundamental group is π1(Spec k), the fundamental group of a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k. Essentially by definition, the fundamental group of k can be shown to be isomorphic to the absolute Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
Gal (ksep / k). More precisely, the choice of a geometric point of Spec (k) is equivalent to giving a separably closed extension field K, and the fundamental group with respect to that base point identifies with the Galois group Gal (K / k). This interpretation of the Galois group is known as Grothendieck's Galois theory
Grothendieck's Galois theory
In mathematics, Grothendieck's Galois theory is a highly abstract approach to the Galois theory of fields, developed around 1960 to provide a way to study the fundamental group of algebraic topology in the setting of algebraic geometry...
.
More generally, for any geometrically connected variety X over a field k (i.e., X is such that Xsep := X ×k ksep is connected) there is an exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
of profinite groups
- 1 → π1(Xsep) → π1(X) → Gal(ksep / k) → 1.
Schemes over a field of characteristic zero
For a scheme X that is of finite type over C, the complex numbers, there is a close relation between the etale (also called algebraic) fundamental group of X and the usual, topological, fundamental group of X(C), the complex analytic spaceComplex analytic space
In mathematics, a complex analytic space is a generalization of a complex manifold which allows the presence of singularities. Complex analytic spaces are locally ringed spaces which are locally isomorphic to local model spaces, where a local model space is an open subset of the vanishing locus of...
attached to X. The algebraic fundamental group, as it is typically called in this case, is the profinite completion of π1(X). This is a consequence of the Riemann existence theorem, which says that all finite etale coverings of X(C) stem from ones of X. In particular, as the fundamental group of smooth curves over C (i.e., open Riemann surfaces) is well-understood, this determines the algebraic fundamental group. More generally, the fundamental group of a proper scheme over any algebraically closed field of characteristic zero is known, because an extension of algebraically closed fields induces isomorphic fundamental groups.
Schemes over a field of positive characteristic and the tame fundamental group
For an algebraically closed field k of positive characteristic, the results are different, since Artin-Schreier coverings exist in this situation. For example, the fundamental group of the affine line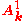 is not topologically finitely generated. The tame fundamental group of some scheme U is a quotient of the usual fundamental group of U which takes into account only covers that are tamely ramified along D, where X is some compactification and D is the complement of U in X. For example, the tame fundamental group of the affine line is zero.
is not topologically finitely generated. The tame fundamental group of some scheme U is a quotient of the usual fundamental group of U which takes into account only covers that are tamely ramified along D, where X is some compactification and D is the complement of U in X. For example, the tame fundamental group of the affine line is zero.Further topics
From a categoricCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
point of view, the fundamental group is a functor
- {Algebraic Varieties} → {Profinite groups}.
The inverse Galois problem
Inverse Galois problem
In Galois theory, the inverse Galois problem concerns whether or not every finite group appears as the Galois group of some Galois extension of the rational numbers Q. This problem, first posed in the 19th century, is unsolved....
asks what groups can arise as fundamental groups (or Galois groups of field extensions). Anabelian geometry
Anabelian geometry
Anabelian geometry is a proposed theory in mathematics, describing the way the algebraic fundamental group G of an algebraic variety V, or some related geometric object, determines how V can be mapped into another geometric object W, under the assumption that G is very far from being an abelian...
, for example Grothendieck's section conjecture, seeks to identify classes of varieties which are determined by their fundamental groups.
See also
- étale morphismÉtale morphismIn algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
- Topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
- Fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
- Classification of covering spaces
- Fundamental group schemeFundamental group schemeIn mathematics, the fundamental group scheme is a group scheme canonically associated to a scheme over a Dedekind scheme . It is a generalisation of the étale fundamental group...
- étale homotopy theory

