
Étale morphism
Encyclopedia
In algebraic geometry
, a field of mathematics
, an étale morphism (etal) is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem
, but because open sets in the Zariski topology
are so large, they are not necessarily local isomorphisms. Despite this, étale maps retain many of the properties of local analytic isomorphisms, and are useful in defining the algebraic fundamental group and the étale topology
.
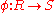 be a ring homomorphism
be a ring homomorphism
. This makes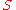 an
an  -algebra. Choose a monic polynomial
-algebra. Choose a monic polynomial  in
in 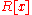 and a polynomial
and a polynomial 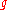 in
in 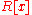 such that the derivative
such that the derivative
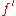 of
of  is a unit in the localization
is a unit in the localization
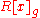 . We say that
. We say that  is standard étale if
is standard étale if  and
and 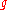 can be chosen so that
can be chosen so that 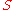 is isomorphic as an
is isomorphic as an  -algebra to
-algebra to 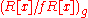 . Geometrically, this represents
. Geometrically, this represents  as an open subset of a covering space.
as an open subset of a covering space.
Let be a morphism of schemes. We say that
be a morphism of schemes. We say that  is étale if it has any of the following equivalent properties:
is étale if it has any of the following equivalent properties:
Assume that is locally noetherian and f is locally of finite type. For
is locally noetherian and f is locally of finite type. For  in
in  , let
, let 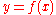 and let
and let  be the induced map on completed
be the induced map on completed
local rings. Then the following are equivalent:
If in addition all the maps on residue fields are isomorphisms, or if
are isomorphisms, or if 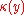 is separably closed, then
is separably closed, then  is étale if and only if for every
is étale if and only if for every  in
in  , the induced map on completed local rings is an isomorphism.
, the induced map on completed local rings is an isomorphism.
Morphisms induced by finite separable field extensions are étale.
Any ring homomorphism of the form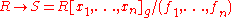 , where
, where  is noetherian, all the
is noetherian, all the 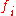 are polynomials, and where the Jacobian determinant
are polynomials, and where the Jacobian determinant 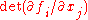 is a unit in
is a unit in 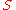 , is étale.
, is étale.
Expanding upon the previous example, suppose that we have a morphism of smooth complex algebraic varieties. Since
of smooth complex algebraic varieties. Since  is given by equations, we can interpret it as a map of complex manifolds. Whenever the Jacobian of
is given by equations, we can interpret it as a map of complex manifolds. Whenever the Jacobian of  is nonzero,
is nonzero,  is a local isomorphism of complex manifolds by the implicit function theorem
is a local isomorphism of complex manifolds by the implicit function theorem
. By the previous example, having non-zero Jacobian is the same as being étale.
Let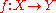 be a dominant morphism of finite type with X, Y locally noetherian, irreducible and Y normal. If f is unramified, then it is étale.
be a dominant morphism of finite type with X, Y locally noetherian, irreducible and Y normal. If f is unramified, then it is étale.
For a field K, any K-algebra A is necessarily flat. Therefore, A is an etale algebra if and only if it is unramified, which is also equivalent to
where is the separable closure of the field K and the right hand side is a finite direct sum, all of whose summands are
is the separable closure of the field K and the right hand side is a finite direct sum, all of whose summands are  . This characterization of etale K-algebras is a stepping stone in reinterpreting classical Galois theory
. This characterization of etale K-algebras is a stepping stone in reinterpreting classical Galois theory
(see Grothendieck's Galois theory
).
are the algebraic counterpart of local diffeomorphisms. More precisely, a morphism between smooth varieties is étale at a point iff the differential between the corresponding tangent space
s is an isomorphism. This is in turn precisely the condition needed to ensure that a map between manifold
s is a local diffeomorphism, i.e. for any point y ∈ Y, there is an open neighborhood U of x such that the restriction of f to U is a diffeomorphism. This conclusion does not hold in algebraic geometry, because the topology is too coarse. For example, consider the projection f of the parabola
to the y-axis. This morphism is étale at every point except the origin (0, 0), because the differential is given by 2x, which does not vanish at these points.
However, there is no (Zariski-
)local inverse of f, just because the square root
is not an algebraic map, not being given by polynomials. However, there is a remedy for this situation, using the étale topology. The precise statement is as follows: if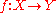 is étale and quasi-compact, then for any point y lying in f(X), there is an étale morphism V → Y containing y in its image (V can be thought of as an étale open neighborhood of y), such that when we base change f to V, then
is étale and quasi-compact, then for any point y lying in f(X), there is an étale morphism V → Y containing y in its image (V can be thought of as an étale open neighborhood of y), such that when we base change f to V, then  (the first member would be the pre-image of V by f if V were a Zariski open neighborhood) is a finite disjoint union of open subsets isomorphic to V. In other words, étale-locally in Y, the morphism f is a topological finite cover.
(the first member would be the pre-image of V by f if V were a Zariski open neighborhood) is a finite disjoint union of open subsets isomorphic to V. In other words, étale-locally in Y, the morphism f is a topological finite cover.
For a smooth morphism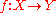 of relative dimension n, étale-locally in X and in Y, f is an open immersion into an affine space
of relative dimension n, étale-locally in X and in Y, f is an open immersion into an affine space  . This is the étale analogue version of the structure theorem on submersions.
. This is the étale analogue version of the structure theorem on submersions.
, which means "slack", as in "slack tide", or, figuratively, calm, immobile, something left to settle.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a field of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an étale morphism (etal) is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
, but because open sets in the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
are so large, they are not necessarily local isomorphisms. Despite this, étale maps retain many of the properties of local analytic isomorphisms, and are useful in defining the algebraic fundamental group and the étale topology
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
.
Definition
Let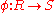 be a ring homomorphism
be a ring homomorphismRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
. This makes
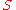 an
an  -algebra. Choose a monic polynomial
-algebra. Choose a monic polynomial  in
in 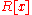 and a polynomial
and a polynomial 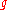 in
in 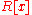 such that the derivative
such that the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
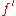 of
of  is a unit in the localization
is a unit in the localizationLocalization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
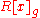 . We say that
. We say that  is standard étale if
is standard étale if  and
and 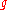 can be chosen so that
can be chosen so that 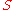 is isomorphic as an
is isomorphic as an  -algebra to
-algebra to 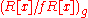 . Geometrically, this represents
. Geometrically, this represents  as an open subset of a covering space.
as an open subset of a covering space.Let
 be a morphism of schemes. We say that
be a morphism of schemes. We say that  is étale if it has any of the following equivalent properties:
is étale if it has any of the following equivalent properties:
-
 is flatFlat morphismIn mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,is a flat map for all P in X...
is flatFlat morphismIn mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,is a flat map for all P in X...
and unramified. -
 is a smooth morphism and unramified.
is a smooth morphism and unramified. -
 is flat, locally of finite presentation, and for every
is flat, locally of finite presentation, and for every 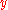 in
in  , the fiber
, the fiber 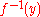 is the disjoint union of points, each of which is the spectrum of a finite separable field extension of the residue field
is the disjoint union of points, each of which is the spectrum of a finite separable field extension of the residue field  .
. -
 is flat, locally of finite presentation, and for every
is flat, locally of finite presentation, and for every 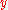 in
in  and every algebraic closure
and every algebraic closure 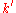 of the residue field
of the residue field 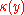 , the geometric fiber
, the geometric fiber 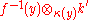 is the disjoint union of points, each of which is isomorphic to
is the disjoint union of points, each of which is isomorphic to 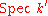 .
. -
 is a smooth morphism of relative dimension zero.
is a smooth morphism of relative dimension zero. -
 is a smooth morphism and a locally quasi-finite morphismQuasi-finite morphismIn algebraic geometry, a branch of mathematics, a morphism f : X → Y of schemes is quasi-finite if it is finite type and satisfies any of the following equivalent conditions:...
is a smooth morphism and a locally quasi-finite morphismQuasi-finite morphismIn algebraic geometry, a branch of mathematics, a morphism f : X → Y of schemes is quasi-finite if it is finite type and satisfies any of the following equivalent conditions:...
. -
 is locally of finite presentation and is locally a standard étale morphism, that is,
is locally of finite presentation and is locally a standard étale morphism, that is,
- For every
 in
in  , let
, let 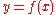 . Then there is an open affine neighborhood of
. Then there is an open affine neighborhood of 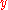 and an open affine neighborhood of
and an open affine neighborhood of  such that is contained in and such that the ring homomorphism induced by
such that is contained in and such that the ring homomorphism induced by  is standard étale.
is standard étale.
- For every
-
 is locally of finite presentation and is formally étaleFormally étale morphismIn commutative algebra and algebraic geometry, a morphism is called formally étale if has a lifting property that is analogous to being a local diffeomorphism.- Formally étale homomorphisms of rings :...
is locally of finite presentation and is formally étaleFormally étale morphismIn commutative algebra and algebraic geometry, a morphism is called formally étale if has a lifting property that is analogous to being a local diffeomorphism.- Formally étale homomorphisms of rings :...
. -
 is locally of finite presentation and is formally étale for maps from local rings, that is:
is locally of finite presentation and is formally étale for maps from local rings, that is:
- Let A be a local ring and J be an ideal of A such that . Set and , and let be the canonical closed immersion. Let z denote the closed point of Z0. Let and be morphisms such that . Then there exists a unique Y-morphism such that .
Assume that
 is locally noetherian and f is locally of finite type. For
is locally noetherian and f is locally of finite type. For  in
in  , let
, let 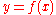 and let
and let  be the induced map on completed
be the induced map on completedCompletion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
local rings. Then the following are equivalent:
-
 is étale.
is étale. - For every
 in
in  , the induced map on completed local rings is formally étale for the adic topology.
, the induced map on completed local rings is formally étale for the adic topology. - For every
 in
in  ,
, 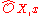 is a free
is a free  -module and the fiber
-module and the fiber 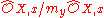 is a field which is a finite separable field extension of the residue field
is a field which is a finite separable field extension of the residue field 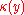 . (Here
. (Here 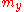 is the maximal ideal of
is the maximal ideal of 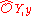 .)
.) - f is formally étale for maps of local rings with the following additional properties. The local ring A may be assumed Artinian. If m is the maximal ideal of A, then J may be assumed to satisfy . Finally, the morphism on residue fields may be assumed to be an isomorphism.
If in addition all the maps on residue fields
 are isomorphisms, or if
are isomorphisms, or if 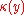 is separably closed, then
is separably closed, then  is étale if and only if for every
is étale if and only if for every  in
in  , the induced map on completed local rings is an isomorphism.
, the induced map on completed local rings is an isomorphism.Examples of étale morphisms
Any open immersion is étale because it is locally an isomorphism.Morphisms induced by finite separable field extensions are étale.
Any ring homomorphism of the form
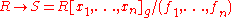 , where
, where  is noetherian, all the
is noetherian, all the 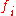 are polynomials, and where the Jacobian determinant
are polynomials, and where the Jacobian determinant 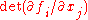 is a unit in
is a unit in 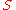 , is étale.
, is étale.Expanding upon the previous example, suppose that we have a morphism
 of smooth complex algebraic varieties. Since
of smooth complex algebraic varieties. Since  is given by equations, we can interpret it as a map of complex manifolds. Whenever the Jacobian of
is given by equations, we can interpret it as a map of complex manifolds. Whenever the Jacobian of  is nonzero,
is nonzero,  is a local isomorphism of complex manifolds by the implicit function theorem
is a local isomorphism of complex manifolds by the implicit function theoremImplicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
. By the previous example, having non-zero Jacobian is the same as being étale.
Let
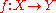 be a dominant morphism of finite type with X, Y locally noetherian, irreducible and Y normal. If f is unramified, then it is étale.
be a dominant morphism of finite type with X, Y locally noetherian, irreducible and Y normal. If f is unramified, then it is étale.For a field K, any K-algebra A is necessarily flat. Therefore, A is an etale algebra if and only if it is unramified, which is also equivalent to

where
 is the separable closure of the field K and the right hand side is a finite direct sum, all of whose summands are
is the separable closure of the field K and the right hand side is a finite direct sum, all of whose summands are  . This characterization of etale K-algebras is a stepping stone in reinterpreting classical Galois theory
. This characterization of etale K-algebras is a stepping stone in reinterpreting classical Galois theoryGalois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
(see Grothendieck's Galois theory
Grothendieck's Galois theory
In mathematics, Grothendieck's Galois theory is a highly abstract approach to the Galois theory of fields, developed around 1960 to provide a way to study the fundamental group of algebraic topology in the setting of algebraic geometry...
).
Properties of étale morphisms
- Étale morphisms are preserved under composition and base change.
- Étale morphisms are local on the source and on the base. In other words,
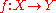 is étale if and only if for each covering of
is étale if and only if for each covering of  by open subschemes the restriction of
by open subschemes the restriction of  to each of the open subschemes of the covering is étale, and also if and only if for each cover of
to each of the open subschemes of the covering is étale, and also if and only if for each cover of  by open subschemes the induced morphisms
by open subschemes the induced morphisms 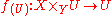 is étale for each subscheme
is étale for each subscheme  of the covering. In particular, it is possible to test the property of being étale on open affines
of the covering. In particular, it is possible to test the property of being étale on open affines  .
. - The product of a finite family of étale morphisms is étale.
- Given a finite family of morphisms
 , the disjoint union
, the disjoint union 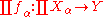 is étale if and only if each
is étale if and only if each 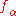 is étale.
is étale. - Let
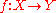 and
and  , and assume that
, and assume that 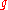 is unramified and
is unramified and 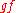 is étale. Then
is étale. Then  is étale. In particular, if
is étale. In particular, if  and
and 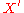 are étale over
are étale over  , then any
, then any  -morphism between
-morphism between  and
and 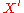 is étale.
is étale. - Quasi-compact étale morphisms are quasi-finiteQuasi-finite morphismIn algebraic geometry, a branch of mathematics, a morphism f : X → Y of schemes is quasi-finite if it is finite type and satisfies any of the following equivalent conditions:...
. - A morphism
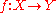 is an open immersion if and only if it is étale and radicialRadicial morphismIn algebraic geometry, a domain in mathematics, a morphism of schemesis called radicial or universally injective, if, for every field K the induced map X → Y is injective...
is an open immersion if and only if it is étale and radicialRadicial morphismIn algebraic geometry, a domain in mathematics, a morphism of schemesis called radicial or universally injective, if, for every field K the induced map X → Y is injective...
. - If
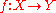 is étale and surjective, then
is étale and surjective, then  (finite or otherwise).
(finite or otherwise).
Étale morphisms and the inverse function theorem
As said in the introduction, étale morphisms- f: X → Y
are the algebraic counterpart of local diffeomorphisms. More precisely, a morphism between smooth varieties is étale at a point iff the differential between the corresponding tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s is an isomorphism. This is in turn precisely the condition needed to ensure that a map between manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s is a local diffeomorphism, i.e. for any point y ∈ Y, there is an open neighborhood U of x such that the restriction of f to U is a diffeomorphism. This conclusion does not hold in algebraic geometry, because the topology is too coarse. For example, consider the projection f of the parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
- y = x2
to the y-axis. This morphism is étale at every point except the origin (0, 0), because the differential is given by 2x, which does not vanish at these points.
However, there is no (Zariski-
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
)local inverse of f, just because the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
is not an algebraic map, not being given by polynomials. However, there is a remedy for this situation, using the étale topology. The precise statement is as follows: if
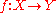 is étale and quasi-compact, then for any point y lying in f(X), there is an étale morphism V → Y containing y in its image (V can be thought of as an étale open neighborhood of y), such that when we base change f to V, then
is étale and quasi-compact, then for any point y lying in f(X), there is an étale morphism V → Y containing y in its image (V can be thought of as an étale open neighborhood of y), such that when we base change f to V, then  (the first member would be the pre-image of V by f if V were a Zariski open neighborhood) is a finite disjoint union of open subsets isomorphic to V. In other words, étale-locally in Y, the morphism f is a topological finite cover.
(the first member would be the pre-image of V by f if V were a Zariski open neighborhood) is a finite disjoint union of open subsets isomorphic to V. In other words, étale-locally in Y, the morphism f is a topological finite cover.For a smooth morphism
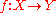 of relative dimension n, étale-locally in X and in Y, f is an open immersion into an affine space
of relative dimension n, étale-locally in X and in Y, f is an open immersion into an affine space  . This is the étale analogue version of the structure theorem on submersions.
. This is the étale analogue version of the structure theorem on submersions.Etymology
The word étale is a French adjectiveAdjective
In grammar, an adjective is a 'describing' word; the main syntactic role of which is to qualify a noun or noun phrase, giving more information about the object signified....
, which means "slack", as in "slack tide", or, figuratively, calm, immobile, something left to settle.

