
Fundamental group scheme
Encyclopedia
In mathematics, the fundamental group scheme is a group scheme
canonically associated to a scheme
over a Dedekind scheme (e.g. the spectrum of a field
or the spectrum of a discrete valuation ring
). It is a generalisation of the étale fundamental group
. Although its existence was conjectured by Alexander Grothendieck
, the first construction is due to Madhav Nori, who only worked on schemes over fields. A generalisation to schemes over Dedekind scheme is due to Carlo Gasbarri.
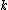 be a perfect field and
be a perfect field and 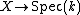 a faithfully flat and proper morphism of schemes with
a faithfully flat and proper morphism of schemes with 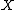 a reduced and connected scheme. Assume the existence of a section
a reduced and connected scheme. Assume the existence of a section  , then the fundamental group scheme
, then the fundamental group scheme 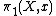 of
of 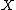 in
in  is defined as the affine group scheme naturally associated to the neutral tannakian category
is defined as the affine group scheme naturally associated to the neutral tannakian category
(over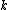 ) of essentially finite vector bundle
) of essentially finite vector bundle
s over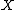 .
.
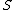 be a connected Dedekind scheme and
be a connected Dedekind scheme and  a faithfully flat and proper morphism of schemes with
a faithfully flat and proper morphism of schemes with 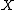 integral. Assume the existence of a section
integral. Assume the existence of a section  . Once we prove that the category
. Once we prove that the category
of isomorphism classes of torsors over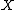 (pointed over
(pointed over  ) under the action of finite and flat
) under the action of finite and flat 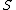 -group scheme
-group scheme
s is cofiltered then we define the universal torsor (pointed over ) as the projective limit of all the torsors of that category. The
) as the projective limit of all the torsors of that category. The 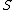 -group scheme acting on it is called the fundamental group scheme and denoted by
-group scheme acting on it is called the fundamental group scheme and denoted by 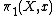 (when
(when 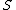 is the spectrum of a perfect field the two definitions coincide so that no confusion can arise).
is the spectrum of a perfect field the two definitions coincide so that no confusion can arise).
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
canonically associated to a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
over a Dedekind scheme (e.g. the spectrum of a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
or the spectrum of a discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
). It is a generalisation of the étale fundamental group
Étale fundamental group
The étale fundamental group is an analogue in algebraic geometry, for schemes, of the usual fundamental group of topological spaces.-Topological analogue:In algebraic topology, the fundamental group\pi_1...
. Although its existence was conjectured by Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
, the first construction is due to Madhav Nori, who only worked on schemes over fields. A generalisation to schemes over Dedekind scheme is due to Carlo Gasbarri.
First definition
Let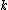 be a perfect field and
be a perfect field and 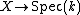 a faithfully flat and proper morphism of schemes with
a faithfully flat and proper morphism of schemes with 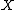 a reduced and connected scheme. Assume the existence of a section
a reduced and connected scheme. Assume the existence of a section  , then the fundamental group scheme
, then the fundamental group scheme 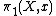 of
of 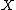 in
in  is defined as the affine group scheme naturally associated to the neutral tannakian category
is defined as the affine group scheme naturally associated to the neutral tannakian categoryTannakian category
In mathematics, a tannakian category is a particular kind of monoidal category C, equipped with some extra structure relative to a given field K. The role of such categories C is to approximate, in some sense, the category of linear representations of an algebraic group G defined over K...
(over
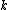 ) of essentially finite vector bundle
) of essentially finite vector bundleEssentially finite vector bundle
In mathematics, an essentially finite vector bundle is a particular type of vector bundle defined by Madhav Nori, as the main tool in the construction of the fundamental group scheme. Even if the definition is not intuitive there is a nice characterization that makes essentially finite vector...
s over
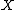 .
.Second definition
Let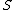 be a connected Dedekind scheme and
be a connected Dedekind scheme and  a faithfully flat and proper morphism of schemes with
a faithfully flat and proper morphism of schemes with 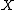 integral. Assume the existence of a section
integral. Assume the existence of a section  . Once we prove that the category
. Once we prove that the categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of isomorphism classes of torsors over
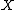 (pointed over
(pointed over  ) under the action of finite and flat
) under the action of finite and flat 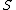 -group scheme
-group schemeGroup scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
s is cofiltered then we define the universal torsor (pointed over
 ) as the projective limit of all the torsors of that category. The
) as the projective limit of all the torsors of that category. The 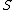 -group scheme acting on it is called the fundamental group scheme and denoted by
-group scheme acting on it is called the fundamental group scheme and denoted by 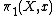 (when
(when 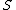 is the spectrum of a perfect field the two definitions coincide so that no confusion can arise).
is the spectrum of a perfect field the two definitions coincide so that no confusion can arise).

