Complex analytic space
Encyclopedia
In mathematics
, a complex analytic space is a generalization of a complex manifold
which allows the presence of singularities
. Complex analytic spaces are locally ringed spaces which are locally isomorphic to local model spaces, where a local model space is an open subset of the vanishing locus of a finite set of holomorphic functions.
on a topological space with value C by
. A C-space is a locally ringed space 
whose structure sheaf is an algebra
over
.
Choose an open subset U of some complex affine space Cn, and fix finitely many holomorphic functions f1, ..., fk in U. Let X = V(f1, ..., fk) be the common vanishing locus of these holomorphic functions, that is, X = {x|f1(x) = ... = fk(x) = 0}. Define a sheaf of rings on X by letting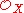
be the restriction to X of 
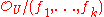, where 
is the sheaf of holomorphic functions on U. Then the locally ringed C-space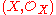 
is a local model space.
A complex analytic space is a locally ringed C-space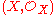
which is locally isomorphic to a local model space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a complex analytic space is a generalization of a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
which allows the presence of singularities
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
. Complex analytic spaces are locally ringed spaces which are locally isomorphic to local model spaces, where a local model space is an open subset of the vanishing locus of a finite set of holomorphic functions.
Definition
Denote the constant sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on a topological space with value C by
. A C-space is a locally ringed space whose structure sheaf is an algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over
.Choose an open subset U of some complex affine space Cn, and fix finitely many holomorphic functions f1, ..., fk in U. Let X = V(f1, ..., fk) be the common vanishing locus of these holomorphic functions, that is, X = {x|f1(x) = ... = fk(x) = 0}. Define a sheaf of rings on X by letting
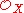be the restriction to X of 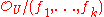, where is the sheaf of holomorphic functions on U. Then the locally ringed C-space 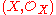is a local model space.A complex analytic space is a locally ringed C-space
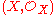which is locally isomorphic to a local model space.