Metaplectic group
Encyclopedia
In mathematics
, the metaplectic group Mp2n is a double cover of the symplectic group
Sp2n. It can be defined over either real
or p-adic numbers. The construction covers more generally the case of an arbitrary local
or finite
field, and even the ring of adeles
.
The metaplectic group has a particularly significant infinite-dimensional linear representation, the Weil representation . It was used by André Weil
to give a representation-theoretic interpretation of theta functions, and is important in the theory of modular form
s of half-integral weight and the theta correspondence.
of the symplectic Lie group Sp2n(R) is infinite cyclic, so it has a unique connected double cover, which is denoted Mp2n(R) and called the metaplectic group.
The metaplectic group Mp2(R) is not a matrix group
: it has no faithful finite-dimensional representation
s. Therefore, the question of its explicit realization is nontrivial. It has faithful irreducible infinite-dimensional representations, such as the Weil representation described below.
It can be proved that if F is any local field other than C, then the symplectic group Sp2n(F) admits a unique perfect
central extension with the kernel Z/2Z, the cyclic group of order 2, which is called the metaplectic group over F.
It serves as an algebraic replacement of the topological notion of a 2-fold cover used when F=R. The approach through the notion of central extension is useful even in the case of real metaplectic group, because it allows a description of the group operation via a certain cocycle
.
SL2(R). This group biholomorphically acts on the complex upper half-plane by fractional-linear transformations,
is a real 2 by 2 matrix with the unit determinant and z is in the upper half-plane, and this action can be used to explicitly construct the metaplectic cover of SL2(R).
The elements of the metaplectic group Mp2(R) are the pairs (g, ε), where
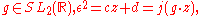
so that ε is a choice of one of the two branches of the complex square root function of j (g z) for z in the complex upper half-plane. The multiplication law is defined by:
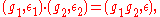where 
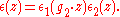
The associativity of this product follows from a certain cocycle condition satisfied by ε(z). The map
is a surjection from Mp2(R) to SL2(R) which does not admit a continuous section. Hence, we have constructed a non-trivial 2-fold cover of the latter group.
on a Hilbert space
, that is,
with the center acting as a given nonzero constant. The Stone-von Neumann theorem states that this representation is essentially unique: if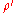
is another such representation, there exists an automorphism
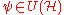such that 
.
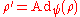and the conjugating automorphism is projectively unique, ie. up to a multiplicative modulus 1 constant. So any automorphism of the Heisenberg group, inducing the identity on the center, acts on this representation
---to be precise, the action is only well-defined up to multiplication by a non-zero constant.
The automorphisms of the Heisenberg group (fixing its center) form the symplectic group, so at first sight this seems to give an action of the symplectic group on
. However, the action is only defined up to multiplication by a nonzero constant, in other words, one can only map the automorphism of the group to the class 
.
So we only get a homomorphism from the symplectic group to the projective unitary group of H; in other words a projective representation
. The general theory of projective representations then applies, to give an action of some central extension of the symplectic group on H. A calculation shows that this central extension can be taken to be a double cover, and this double cover is the metaplectic group.
Now we give a more concrete construction in the simplest case of
Mp2(R). The Hilbert space H is then the space of all L2 functions on the reals. The Heisenberg group is generated by translations and multiplication by the functions eixy of x, for y real. Then the action of the metaplectic group on H is generated by the Fourier transform and multiplication by the functions exp(ix2y) of x, for y real.
Some important examples of this construction are given by:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the metaplectic group Mp2n is a double cover of the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp2n. It can be defined over either real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or p-adic numbers. The construction covers more generally the case of an arbitrary local
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
or finite
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
field, and even the ring of adeles
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
.
The metaplectic group has a particularly significant infinite-dimensional linear representation, the Weil representation . It was used by André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
to give a representation-theoretic interpretation of theta functions, and is important in the theory of modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s of half-integral weight and the theta correspondence.
Definition
The fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the symplectic Lie group Sp2n(R) is infinite cyclic, so it has a unique connected double cover, which is denoted Mp2n(R) and called the metaplectic group.
The metaplectic group Mp2(R) is not a matrix group
Matrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
: it has no faithful finite-dimensional representation
Faithful representation
In mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ.In more abstract language, this means...
s. Therefore, the question of its explicit realization is nontrivial. It has faithful irreducible infinite-dimensional representations, such as the Weil representation described below.
It can be proved that if F is any local field other than C, then the symplectic group Sp2n(F) admits a unique perfect
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
central extension with the kernel Z/2Z, the cyclic group of order 2, which is called the metaplectic group over F.
It serves as an algebraic replacement of the topological notion of a 2-fold cover used when F=R. The approach through the notion of central extension is useful even in the case of real metaplectic group, because it allows a description of the group operation via a certain cocycle
Cocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
.
Explicit construction for n=1
In the case n=1, the symplectic group coincides with the special linear groupSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL2(R). This group biholomorphically acts on the complex upper half-plane by fractional-linear transformations,
-
where 
is a real 2 by 2 matrix with the unit determinant and z is in the upper half-plane, and this action can be used to explicitly construct the metaplectic cover of SL2(R).
The elements of the metaplectic group Mp2(R) are the pairs (g, ε), where
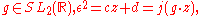
so that ε is a choice of one of the two branches of the complex square root function of j (g z) for z in the complex upper half-plane. The multiplication law is defined by:
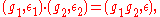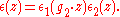
where The associativity of this product follows from a certain cocycle condition satisfied by ε(z). The map
is a surjection from Mp2(R) to SL2(R) which does not admit a continuous section. Hence, we have constructed a non-trivial 2-fold cover of the latter group.
Construction of the Weil representation
We first give a rather abstract reason why the Weil representation exists. The Heisenberg group has an irreducible unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
on a Hilbert space
, that is,with the center acting as a given nonzero constant. The Stone-von Neumann theorem states that this representation is essentially unique: if
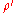is another such representation, there exists an automorphism 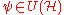such that 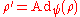.and the conjugating automorphism is projectively unique, ie. up to a multiplicative modulus 1 constant. So any automorphism of the Heisenberg group, inducing the identity on the center, acts on this representation
---to be precise, the action is only well-defined up to multiplication by a non-zero constant.The automorphisms of the Heisenberg group (fixing its center) form the symplectic group, so at first sight this seems to give an action of the symplectic group on
. However, the action is only defined up to multiplication by a nonzero constant, in other words, one can only map the automorphism of the group to the class .So we only get a homomorphism from the symplectic group to the projective unitary group of H; in other words a projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
. The general theory of projective representations then applies, to give an action of some central extension of the symplectic group on H. A calculation shows that this central extension can be taken to be a double cover, and this double cover is the metaplectic group.
Now we give a more concrete construction in the simplest case of
Mp2(R). The Hilbert space H is then the space of all L2 functions on the reals. The Heisenberg group is generated by translations and multiplication by the functions eixy of x, for y real. Then the action of the metaplectic group on H is generated by the Fourier transform and multiplication by the functions exp(ix2y) of x, for y real.
Generalizations
Weil showed how to extend the theory above by replacing R by any locally compact group G that is isomorphic to its Pontryagin dual (the group of characters). The Hilbert space H is then the space of all L2 functions on G. The (analogue of) the Heisenberg group is generated by translations by elements of G, and multiplication by elements of the dual group (considered as functions from G to the unit circle). There is an analogue of the symplectic group acting on the Heisenberg group, and this action lifts to a projective representation on H. The corresponding central extension of the symplectic group is called the metaplectic group.Some important examples of this construction are given by:
- G is a vector space over the reals of dimension n. This gives a metaplectic group that is a double cover of the symplectic group Sp2n(R).
- More generally G can be a vector space over any local fieldLocal fieldIn mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
F of dimension n. This gives a metaplectic group that is a double cover of the symplectic group Sp2n(F).
- G is a vector space over the adelesAdele ringIn algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
of a number field (or global fieldGlobal fieldIn mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
). This case is used in the representation-theoretic approach to automorphic formAutomorphic formIn mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s.
- G is a finite group. The corresponding metaplectic group is then also finite, and the central cover is trivial. This case is used in the theory of theta functions of lattices, where typically G will be the discriminant group of an even latticeLattice (group)In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
.
- A modern point of view on the existence of the linear (not projective) Weil representation over a finite field, namely, that it admits a canonical Hilbert space realization, was proposed by David KazhdanDavid KazhdanDavid Kazhdan or Každan, Kazhdan, formerly named Dmitry Aleksandrovich Kazhdan , is a Soviet and Israeli mathematician known for work in representation theory.-Life:...
. Using the notion of canonical intertwining operators suggested by Joseph BernsteinJoseph BernsteinJoseph Bernstein is an Israeli mathematician working at Tel Aviv University. He works in algebraic geometry, representation theory, and number theory....
, such a realization was constructed by Gurevich-Hadanihttp://arxiv.org/abs/0705.4556.
See also
- Heisenberg group
- Metaplectic structureMetaplectic structureIn differential geometry, a metaplectic structure is the symplectic analog of spin structure on orientable Riemannian manifolds. A metaplectic structure on a symplectic manifold allows one to define the symplectic spinor bundle, which is the Hilbert space bundle associated to the metaplectic...
- Reductive dual pairReductive dual pairIn the mathematical field of representation theory, a reductive dual pair is a pair of subgroups of the isometry group Sp of a symplectic vector space W, such that G is the centralizer of G ′ in Sp and vice versa, and these groups act reductively on W...
- Spin group, another double cover
- Symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
- Theta function