
G-structure
Encyclopedia
In differential geometry, a G-structure on an n-manifold
M, for a given structure group G, is a G-subbundle
of the tangent frame bundle FM (or GL(M)) of M.
The notion of G-structures includes many other structures on manifolds, some of them being defined by tensor field
s. For example, for the orthogonal group
, an O(n)-structure defines a Riemannian metric, and for the special linear group
an SL(n,R)-structure is the same as a volume form
. For the trivial group
, an {e}-structure consists of an absolute parallelism of the manifold.
Several structures on manifolds, such as a complex structure, a symplectic structure, or a Kähler structure
, are G-structures with an additional integrability condition.
s plays an important role in the study of G-structures, the two notions are different. A G-structure is a principal subbundle of the tangent frame bundle, but the fact that the G-structure bundle consists of tangent frames is regarded as part of the data. For example, consider two Riemannian metrics on Rn. The associated O(n)-structures are isomorphic if and only if the metrics are isometric. But, since Rn is contractible, the underlying O(n)-bundles are always going to be isomorphic as principal bundles.
This fundamental difference between the two theories can be captured by giving an additional piece of data on the underlying G-bundle of a G-structure: the solder form
. The solder form is what ties the underlying principal bundle of the G-structure to the local geometry of the manifold itself by specifying a canonical isomorphism of the tangent bundle of M to an associated vector bundle
. Although the solder form is not a connection form
, it can sometimes be regarded as a precursor to one.
In detail, suppose that Q is the principal bundle of a G-structure. If Q is realized as a reduction of the frame bundle of M, then the solder form is given by the pullback of the tautological form of the frame bundle along the inclusion. Abstractly, if one regards Q as a principal bundle independently of its realization as a reduction of the frame bundle, then the solder form consists of a representation ρ of G on Rn and an isomorphism of bundles θ : TM → Q ×ρ Rn.
, are G-structures with an additional integrability condition. Without the corresponding integrability condition, the structure is instead called an "almost" structure, as in an almost complex structure, an almost symplectic structure, or an almost Kähler structure
Specifically, a symplectic manifold
structure is a stronger concept than a G-structure for the symplectic group
. A symplectic structure on a manifold is a two-form
ω on M that is non-degenerate (which is an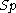 -structure, or almost symplectic structure), together with the extra condition that dω = 0; this latter is called an integrability condition.
-structure, or almost symplectic structure), together with the extra condition that dω = 0; this latter is called an integrability condition.
Similarly, foliation
s correspond to G-structures coming from block matrices
, together with integrability conditions so that the Frobenius theorem
applies.
s of M that preserve a G-structure is called the automorphism group of that structure. For an O(n)-structure they are the group of isometries
of the Riemannian metric and for an SL(n,R)-structure volume preserving maps.
Let P be a G-structure on a manifold M, and Q a G-structure on a manifold N. Then an isomorphism of the G-structures is a diffeomorphism f : M → N such that the pushforward of linear frames f* : FM → FN restricts to give a mapping of P into Q. (Note that it is sufficient that Q be contained within the image of f*.) The G-structures P and Q are locally isomorphic if M admits a covering by open sets U and a family of diffeomorphisms fU : U → f(U) ⊂ N such that fU induces an isomorphism of P|U → Q|f(U).
An automorphism of a G-structure is an isomorphism of a G-structure P with itself. Automorphisms arise frequently in the study of transformation groups of geometric structures, since many of the important geometric structures on a manifold can be realized as G-structures.
A flat G-structure is a G-structure P having a global section (V1,...,Vn) consisting of commuting vector fields
. A G-structure is integrable (or locally flat) if it is locally isomorphic to a flat G-structure.
A wide class of equivalence problems
can be formulated in the language of G-structures. For example, a pair of Riemannian manifolds are (locally) equivalent if and only if their bundles of orthonormal frame
s are (locally) isomorphic G-structures. In this view, the general procedure for solving an equivalence problem is to construct a system of invariants for the G-structure which are then sufficient to determine whether a pair of G-structures are locally isomorphic or not.
on the principal bundle Q induces a connection on any associated vector bundle: in particular on the tangent bundle. A linear connection
∇ on TM arising in this way is said to be compatible with Q. Connections compatible with Q are also called adapted connections.
Concretely speaking, adapted connections can be understood in terms of a moving frame
. Suppose that Vi is a basis of local sections of TM (i.e., a frame on M) which defines a section of Q. Any connection ∇ determines a system of basis-dependent 1-forms ω via
where, as a matrix of 1-forms, ω ∈ Ω1(M)⊗gl(n). An adapted connection is one for which ω takes its values in the Lie algebra g of G.
The difference of two adapted connections is a 1-form on M with values in the adjoint bundle
AdQ. That is to say, the space AQ of adapted connections is an affine space
for Ω1(AdQ).
The torsion of an adapted connection defines a map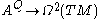
to 2-forms with coefficients in TM. This map is linear; its linearization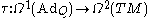
is called the algebraic torsion map. Given two adapted connections ∇ and ∇′, their torsion tensors T∇, T∇′ differ by τ(∇−∇′). Therefore, the image of T∇ in coker(τ) is independent from the choice of ∇.
The image of T∇ in coker(τ) for any adapted connection ∇ is called the torsion of the G-structure. A G-structure is said to be torsion-free if its torsion vanishes. This happens precisely when Q admits a torsion-free adapted connection.
of a structure group of an even-dimensional manifold to GL(n,C). Such a reduction is uniquely determined by a C∞-linear endomorphism J ∈ End(TM) such that J2 = −1. In this situation, the torsion can be computed explicitly as follows.
An easy dimension count shows that ,
,
where Ω2,0(TM) is a space of forms B ∈ Ω2(TM) which satisfy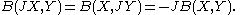
Therefore, the torsion of an almost complex structure can be considered as an element in
Ω2,0(TM). It is easy to check that the torsion of an almost complex structure is equal to its Nijenhuis tensor.
. In such cases, the prolonged G-structure cannot be identified with a G-subbundle of the bundle of linear frames. In many cases, however, the prolongation is a principal bundle in its own right, and its structure group can be identified with a subgroup of a higher-order jet group
. In which case, it is called a higher order G-structure [Kobayashi]. In general, Cartan's equivalence method
applies to such cases.
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M, for a given structure group G, is a G-subbundle
Subbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
of the tangent frame bundle FM (or GL(M)) of M.
The notion of G-structures includes many other structures on manifolds, some of them being defined by tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
s. For example, for the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, an O(n)-structure defines a Riemannian metric, and for the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
an SL(n,R)-structure is the same as a volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
. For the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
, an {e}-structure consists of an absolute parallelism of the manifold.
Several structures on manifolds, such as a complex structure, a symplectic structure, or a Kähler structure
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, are G-structures with an additional integrability condition.
Principal bundles and G-structures
Although the theory of principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s plays an important role in the study of G-structures, the two notions are different. A G-structure is a principal subbundle of the tangent frame bundle, but the fact that the G-structure bundle consists of tangent frames is regarded as part of the data. For example, consider two Riemannian metrics on Rn. The associated O(n)-structures are isomorphic if and only if the metrics are isometric. But, since Rn is contractible, the underlying O(n)-bundles are always going to be isomorphic as principal bundles.
This fundamental difference between the two theories can be captured by giving an additional piece of data on the underlying G-bundle of a G-structure: the solder form
Solder form
In mathematics, more precisely in differential geometry, a soldering of a fibre bundle to a smooth manifold is a manner of attaching the fibres to the manifold in such a way that they can be regarded as tangent...
. The solder form is what ties the underlying principal bundle of the G-structure to the local geometry of the manifold itself by specifying a canonical isomorphism of the tangent bundle of M to an associated vector bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
. Although the solder form is not a connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
, it can sometimes be regarded as a precursor to one.
In detail, suppose that Q is the principal bundle of a G-structure. If Q is realized as a reduction of the frame bundle of M, then the solder form is given by the pullback of the tautological form of the frame bundle along the inclusion. Abstractly, if one regards Q as a principal bundle independently of its realization as a reduction of the frame bundle, then the solder form consists of a representation ρ of G on Rn and an isomorphism of bundles θ : TM → Q ×ρ Rn.
Integrability conditions
Several structures on manifolds, such as a complex structure, a symplectic structure, or a Kähler structureKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, are G-structures with an additional integrability condition. Without the corresponding integrability condition, the structure is instead called an "almost" structure, as in an almost complex structure, an almost symplectic structure, or an almost Kähler structure
Specifically, a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
structure is a stronger concept than a G-structure for the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
. A symplectic structure on a manifold is a two-form
Two-form
In linear algebra, a two-form is another term for a bilinear form, typically used in informal discussions, or sometimes to indicate that the bilinear form is skew-symmetric....
ω on M that is non-degenerate (which is an
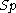 -structure, or almost symplectic structure), together with the extra condition that dω = 0; this latter is called an integrability condition.
-structure, or almost symplectic structure), together with the extra condition that dω = 0; this latter is called an integrability condition.Similarly, foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
s correspond to G-structures coming from block matrices
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
, together with integrability conditions so that the Frobenius theorem
Frobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
applies.
Isomorphism of G-structures
The set of diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s of M that preserve a G-structure is called the automorphism group of that structure. For an O(n)-structure they are the group of isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the Riemannian metric and for an SL(n,R)-structure volume preserving maps.
Let P be a G-structure on a manifold M, and Q a G-structure on a manifold N. Then an isomorphism of the G-structures is a diffeomorphism f : M → N such that the pushforward of linear frames f* : FM → FN restricts to give a mapping of P into Q. (Note that it is sufficient that Q be contained within the image of f*.) The G-structures P and Q are locally isomorphic if M admits a covering by open sets U and a family of diffeomorphisms fU : U → f(U) ⊂ N such that fU induces an isomorphism of P|U → Q|f(U).
An automorphism of a G-structure is an isomorphism of a G-structure P with itself. Automorphisms arise frequently in the study of transformation groups of geometric structures, since many of the important geometric structures on a manifold can be realized as G-structures.
A flat G-structure is a G-structure P having a global section (V1,...,Vn) consisting of commuting vector fields
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
. A G-structure is integrable (or locally flat) if it is locally isomorphic to a flat G-structure.
A wide class of equivalence problems
Cartan's equivalence method
In mathematics, Cartan's equivalence method is a technique in differential geometry for determining whether two geometrical structures are the same up to a diffeomorphism...
can be formulated in the language of G-structures. For example, a pair of Riemannian manifolds are (locally) equivalent if and only if their bundles of orthonormal frame
Orthonormal frame
In Riemannian geometry and relativity theory, an orthonormal frame is a tool for studying the structure of a differentiable manifold equipped with a metric...
s are (locally) isomorphic G-structures. In this view, the general procedure for solving an equivalence problem is to construct a system of invariants for the G-structure which are then sufficient to determine whether a pair of G-structures are locally isomorphic or not.
Connections on G-structures
Let Q be a G-structure on M. A principal connectionConnection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
on the principal bundle Q induces a connection on any associated vector bundle: in particular on the tangent bundle. A linear connection
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
∇ on TM arising in this way is said to be compatible with Q. Connections compatible with Q are also called adapted connections.
Concretely speaking, adapted connections can be understood in terms of a moving frame
Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
. Suppose that Vi is a basis of local sections of TM (i.e., a frame on M) which defines a section of Q. Any connection ∇ determines a system of basis-dependent 1-forms ω via
- ∇X Vi = ωij(X)Vj
where, as a matrix of 1-forms, ω ∈ Ω1(M)⊗gl(n). An adapted connection is one for which ω takes its values in the Lie algebra g of G.
Torsion of a G-structure
Associated to any G-structure is a notion of torsion, related to the torsion of a connection. Note that a given G-structure may admit many different compatible connections which in turn can have different torsions, but in spite of this it is possible to give an independent notion of torsion of the G-structure as follows.The difference of two adapted connections is a 1-form on M with values in the adjoint bundle
Adjoint bundle
In mathematics, an adjoint bundle is a vector bundle naturally associated to any principal bundle. The fibers of the adjoint bundle carry a Lie algebra structure making the adjoint bundle into an algebra bundle...
AdQ. That is to say, the space AQ of adapted connections is an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
for Ω1(AdQ).
The torsion of an adapted connection defines a map
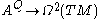
to 2-forms with coefficients in TM. This map is linear; its linearization
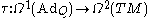
is called the algebraic torsion map. Given two adapted connections ∇ and ∇′, their torsion tensors T∇, T∇′ differ by τ(∇−∇′). Therefore, the image of T∇ in coker(τ) is independent from the choice of ∇.
The image of T∇ in coker(τ) for any adapted connection ∇ is called the torsion of the G-structure. A G-structure is said to be torsion-free if its torsion vanishes. This happens precisely when Q admits a torsion-free adapted connection.
Example: Torsion for almost complex structures
An example of a G-structure is an almost complex structure, that is, a reductionof a structure group of an even-dimensional manifold to GL(n,C). Such a reduction is uniquely determined by a C∞-linear endomorphism J ∈ End(TM) such that J2 = −1. In this situation, the torsion can be computed explicitly as follows.
An easy dimension count shows that
 ,
,where Ω2,0(TM) is a space of forms B ∈ Ω2(TM) which satisfy
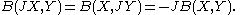
Therefore, the torsion of an almost complex structure can be considered as an element in
Ω2,0(TM). It is easy to check that the torsion of an almost complex structure is equal to its Nijenhuis tensor.
Higher order G-structures
Imposing integrability conditions on a particular G-structure (for instance, with the case of a symplectic form) can be dealt with via the process of prolongationCartan's equivalence method
In mathematics, Cartan's equivalence method is a technique in differential geometry for determining whether two geometrical structures are the same up to a diffeomorphism...
. In such cases, the prolonged G-structure cannot be identified with a G-subbundle of the bundle of linear frames. In many cases, however, the prolongation is a principal bundle in its own right, and its structure group can be identified with a subgroup of a higher-order jet group
Jet group
In mathematics, a jet group is a generalization of the general linear group which applies to Taylor polynomials instead of vectors at a point. Essentially a jet group describes how a Taylor polynomial transforms under changes of coordinate systems .The k-th order jet group Gnk consists of jets of...
. In which case, it is called a higher order G-structure [Kobayashi]. In general, Cartan's equivalence method
Cartan's equivalence method
In mathematics, Cartan's equivalence method is a technique in differential geometry for determining whether two geometrical structures are the same up to a diffeomorphism...
applies to such cases.

