
Branch-decomposition
Encyclopedia
In graph theory
, a branch-decomposition of an undirected graph G is a hierarchical clustering
of the edges of G, represented by an unrooted binary tree
T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way.
The branchwidth of G is the minimum width of any branch-decomposition of G; branchwidth is closely related to tree-width
and many graph optimization problems may be solved efficiently for graphs of small branchwidth. Branch-decompositions and branchwidth may also be generalized from graphs to matroid
s.
is a connected undirected graph with no cycles in which each non-leaf node has exactly three neighbors. A branch-decomposition may be represented by an unrooted binary tree T, together with a bijection between the leaves of T and the edges of the given graph G = (V,E).
If e is any edge of the tree T, then removing e from T partitions it into two subtrees T1 and T2. This partition of T into subtrees induces a partition of the edges associated with the leaves of T into two subgraphs G1 and G2 of G. This partition of G into two subgraphs is called an e-separation.
The width of an e-separation is the number of vertices of G that are incident both to an edge of E1 and to an edge of E2; that is, it is the number of vertices that are shared by the two subgraphs G1 and G2. The width of the branch-decomposition is the maximum width of any of its e-separations. The branchwidth of G is the minimum width of a branch-decomposition of G.
s, and branch-width is closely related to tree-width
: the two quantities are always within a constant factor of each other. In particular, in the paper in which they introduced branch-width, Neil Robertson
and Paul Seymour showed that for a graph G
with tree-width k and branchwidth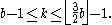
to determine whether a graph G has a branch-decomposition of width at most k, when G and k are both considered as inputs to the problem. However, the graphs with branchwidth at most k form a minor-closed family of graphs
, from which it follows that computing the branchwidth is fixed-parameter tractable
: there is an algorithm for computing optimal branch-decompositions whose running time, on graphs of branchwidth k for any fixed constant k, is linear in the size of the input graph.
For planar graph
s, the branchwidth can be computed exactly in polynomial time., this in contrast to treewidth for which the complexity on planer graphs is a well known open problem.
As with treewidth, branchwidth can be used as the basis of dynamic programming
algorithms for many NP-hard optimization problems, using an amount of time that is exponential in the width of the input graph or matroid. For instance, apply branchwidth-based dynamic programming to a problem of merging multiple partial solutions to the travelling salesman problem
into a single global solution, by forming a sparse graph from the union of the partial solutions, using a spectral clustering heuristic to find a good branch-decomposition of this graph, and applying dynamic programming to the decomposition. argue that branchwidth works better than treewidth in the development of fixed-parameter-tractable algorithms on planar graphs, for multiple reasons: branchwidth may be more tightly bounded by a function of the parameter of interest than the bounds on treewidth, it can be computed exactly in polynomial time rather than merely approximated, and the algorithm for computing it has no large hidden constants.
s that generalizes branch-decompositions of graphs. A branch-decomposition of a matroid is a hierarchical clustering of the matroid elements, represented as an unrooted binary tree with the elements of the matroid at its leaves. An e-separation may be defined in the same way as for graphs, and results in a partition of the set M of matroid elements into two subsets A and B. If ρ denotes the rank function of the matroid, then the width of an e-separation is defined as , and the width of the decomposition and the branchwidth of the matroid are defined analogously. The branchwidth of a graph and the branchwidth of the corresponding graphic matroid may differ: for instance, the three-edge path graph
and the three-edge star
have different branchwidths, 2 and 1 respectively, but they both induce the same graphic matroid with branchwidth 1. However, for graphs that are not trees, the branchwidth of the graph is equal to the branchwidth of its associated graphic matroid. The branchwidth of a matroid is equal to the branchwidth of its dual, and in particular this implies that the branchwidth of any planar graph that is not a tree is equal to that of its dual.
Branchwidth is an important component of attempts to extend the theory of graph minors to matroids: although treewidth can also be generalized to matroids, and plays a bigger role than branchwidth in the theory of graph minors, branchwidth has more convenient properties in the matroid setting. Robertson and Seymour conjectured that the matroids representable over any particular finite field
are well-quasi-ordered
, analogously to the Robertson–Seymour theorem
for graphs, but so far this has been proven only for the matroids of bounded branchwidth. Additionally, if a minor-closed family of matroids representable over a finite field does not include the graphic matroids of all planar graphs, then there is a constant bound on the branchwidth of the matroids in the family, generalizing similar results for minor-closed graph families.
, the graphs of branchwidth k can be characterized by a finite set of forbidden minors. The graphs of branchwidth 0 are the matchings; the minimal forbidden minors are a two-edge path graph
and a triangle graph (or the two-edge cycle, if multigraphs rather than simple graphs are considered). The graphs of branchwidth 1 are the graphs in which each connected component
is a star
; the minimal forbidden minors for branchwidth 1 are the triangle graph (or the two-edge cycle, if multigraphs rather than simple graphs are considered) and the three-edge path graph. The graphs of branchwidth 2 are the graphs in which each biconnected component
is a series-parallel graph
; the only minimal forbidden minor is the complete graph
K4 on four vertices. A graph has branchwidth three if and only if it has treewidth three and does not have the cube graph as a minor; therefore, the four minimal forbidden minors are three of the four forbidden minors for treewidth three (the graph of the octahedron
, the complete graph K5, and the Wagner graph
) together with the cube graph.
Forbidden minors have also been studied for matroid branchwidth, despite the lack of a full analogue to the Robertson–Seymour theorem in this case. A matroid has branchwidth one if and only if every element is either a loop or a coloop, so the unique minimal forbidden minor is the uniform matroid U(2,3), the graphic matroid of the triangle graph. A matroid has branchwidth two if and only if it is the graphic matroid of a graph of branchwidth two, so its minimal forbidden minors are the graphic matroid of K4 and the non-graphic matroid U(2,4). The matroids of branchwidth three are not well-quasi-ordered without the additional assumption of representability over a finite field, but nevertheless the matroids with any finite bound on their branchwidth have finitely many minimal forbidden minors, all of which have a number of elements that is at most exponential in the branchwidth.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a branch-decomposition of an undirected graph G is a hierarchical clustering
Hierarchical clustering
In statistics, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:...
of the edges of G, represented by an unrooted binary tree
Unrooted binary tree
In mathematics and computer science, an unrooted binary tree is an unrooted tree in which each vertex has either one or three neighbors.-Definitions:...
T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way.
The branchwidth of G is the minimum width of any branch-decomposition of G; branchwidth is closely related to tree-width
Tree decomposition
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph...
and many graph optimization problems may be solved efficiently for graphs of small branchwidth. Branch-decompositions and branchwidth may also be generalized from graphs to matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s.
Definitions
An unrooted binary treeUnrooted binary tree
In mathematics and computer science, an unrooted binary tree is an unrooted tree in which each vertex has either one or three neighbors.-Definitions:...
is a connected undirected graph with no cycles in which each non-leaf node has exactly three neighbors. A branch-decomposition may be represented by an unrooted binary tree T, together with a bijection between the leaves of T and the edges of the given graph G = (V,E).
If e is any edge of the tree T, then removing e from T partitions it into two subtrees T1 and T2. This partition of T into subtrees induces a partition of the edges associated with the leaves of T into two subgraphs G1 and G2 of G. This partition of G into two subgraphs is called an e-separation.
The width of an e-separation is the number of vertices of G that are incident both to an edge of E1 and to an edge of E2; that is, it is the number of vertices that are shared by the two subgraphs G1 and G2. The width of the branch-decomposition is the maximum width of any of its e-separations. The branchwidth of G is the minimum width of a branch-decomposition of G.
Relation to treewidth
Branch-decompositions of graphs are closely related to tree decompositionTree decomposition
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph...
s, and branch-width is closely related to tree-width
Tree decomposition
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph...
: the two quantities are always within a constant factor of each other. In particular, in the paper in which they introduced branch-width, Neil Robertson
Neil Robertson (mathematician)
G. Neil Robertson is a mathematician working mainly in topological graph theory, currently a distinguished professor at the Ohio State University. He earned his Ph.D. in 1969 at the University of Waterloo under his doctoral advisor William Tutte. According to the criteria of the Erdős Number...
and Paul Seymour showed that for a graph G
with tree-width k and branchwidth
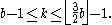
Algorithms and complexity
It is NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
to determine whether a graph G has a branch-decomposition of width at most k, when G and k are both considered as inputs to the problem. However, the graphs with branchwidth at most k form a minor-closed family of graphs
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
, from which it follows that computing the branchwidth is fixed-parameter tractable
Parameterized complexity
Parameterized complexity is a branch of computational complexity theory in computer science that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input. The complexity of a problem is then measured as a function in those...
: there is an algorithm for computing optimal branch-decompositions whose running time, on graphs of branchwidth k for any fixed constant k, is linear in the size of the input graph.
For planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, the branchwidth can be computed exactly in polynomial time., this in contrast to treewidth for which the complexity on planer graphs is a well known open problem.
As with treewidth, branchwidth can be used as the basis of dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
algorithms for many NP-hard optimization problems, using an amount of time that is exponential in the width of the input graph or matroid. For instance, apply branchwidth-based dynamic programming to a problem of merging multiple partial solutions to the travelling salesman problem
Travelling salesman problem
The travelling salesman problem is an NP-hard problem in combinatorial optimization studied in operations research and theoretical computer science. Given a list of cities and their pairwise distances, the task is to find the shortest possible tour that visits each city exactly once...
into a single global solution, by forming a sparse graph from the union of the partial solutions, using a spectral clustering heuristic to find a good branch-decomposition of this graph, and applying dynamic programming to the decomposition. argue that branchwidth works better than treewidth in the development of fixed-parameter-tractable algorithms on planar graphs, for multiple reasons: branchwidth may be more tightly bounded by a function of the parameter of interest than the bounds on treewidth, it can be computed exactly in polynomial time rather than merely approximated, and the algorithm for computing it has no large hidden constants.
Generalization to matroids
It is also possible to define a notion of branch-decomposition for matroidMatroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s that generalizes branch-decompositions of graphs. A branch-decomposition of a matroid is a hierarchical clustering of the matroid elements, represented as an unrooted binary tree with the elements of the matroid at its leaves. An e-separation may be defined in the same way as for graphs, and results in a partition of the set M of matroid elements into two subsets A and B. If ρ denotes the rank function of the matroid, then the width of an e-separation is defined as , and the width of the decomposition and the branchwidth of the matroid are defined analogously. The branchwidth of a graph and the branchwidth of the corresponding graphic matroid may differ: for instance, the three-edge path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
and the three-edge star
Star (graph theory)
In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...
have different branchwidths, 2 and 1 respectively, but they both induce the same graphic matroid with branchwidth 1. However, for graphs that are not trees, the branchwidth of the graph is equal to the branchwidth of its associated graphic matroid. The branchwidth of a matroid is equal to the branchwidth of its dual, and in particular this implies that the branchwidth of any planar graph that is not a tree is equal to that of its dual.
Branchwidth is an important component of attempts to extend the theory of graph minors to matroids: although treewidth can also be generalized to matroids, and plays a bigger role than branchwidth in the theory of graph minors, branchwidth has more convenient properties in the matroid setting. Robertson and Seymour conjectured that the matroids representable over any particular finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
are well-quasi-ordered
Well-quasi-ordering
In mathematics, specifically order theory, a well-quasi-ordering or wqo is a well-founded quasi-ordering with an additional restriction on sequences - that there is no infinite sequence x_i with x_i \not \le x_j for all i...
, analogously to the Robertson–Seymour theorem
Robertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
for graphs, but so far this has been proven only for the matroids of bounded branchwidth. Additionally, if a minor-closed family of matroids representable over a finite field does not include the graphic matroids of all planar graphs, then there is a constant bound on the branchwidth of the matroids in the family, generalizing similar results for minor-closed graph families.
Forbidden minors
By the Robertson–Seymour theoremRobertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
, the graphs of branchwidth k can be characterized by a finite set of forbidden minors. The graphs of branchwidth 0 are the matchings; the minimal forbidden minors are a two-edge path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
and a triangle graph (or the two-edge cycle, if multigraphs rather than simple graphs are considered). The graphs of branchwidth 1 are the graphs in which each connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
is a star
Star (graph theory)
In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...
; the minimal forbidden minors for branchwidth 1 are the triangle graph (or the two-edge cycle, if multigraphs rather than simple graphs are considered) and the three-edge path graph. The graphs of branchwidth 2 are the graphs in which each biconnected component
Biconnected component
In graph theory, a biconnected component is a maximal biconnected subgraph. Any connected graph decomposes into a tree of biconnected components called the block tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or articulation points...
is a series-parallel graph
Series-parallel graph
In graph theory, series-parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.-Definition and terminology:...
; the only minimal forbidden minor is the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K4 on four vertices. A graph has branchwidth three if and only if it has treewidth three and does not have the cube graph as a minor; therefore, the four minimal forbidden minors are three of the four forbidden minors for treewidth three (the graph of the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, the complete graph K5, and the Wagner graph
Wagner graph
In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.-Properties:...
) together with the cube graph.
Forbidden minors have also been studied for matroid branchwidth, despite the lack of a full analogue to the Robertson–Seymour theorem in this case. A matroid has branchwidth one if and only if every element is either a loop or a coloop, so the unique minimal forbidden minor is the uniform matroid U(2,3), the graphic matroid of the triangle graph. A matroid has branchwidth two if and only if it is the graphic matroid of a graph of branchwidth two, so its minimal forbidden minors are the graphic matroid of K4 and the non-graphic matroid U(2,4). The matroids of branchwidth three are not well-quasi-ordered without the additional assumption of representability over a finite field, but nevertheless the matroids with any finite bound on their branchwidth have finitely many minimal forbidden minors, all of which have a number of elements that is at most exponential in the branchwidth.

