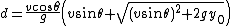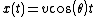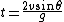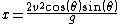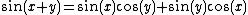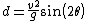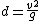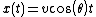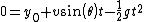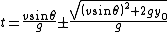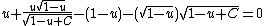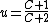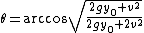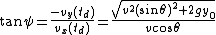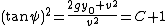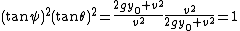In physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, assuming a flat Earth with a uniform gravity field, a projectile

Projectile

A projectile is any object projected into space by the exertion of a force. Although a thrown baseball is technically a projectile too, the term more commonly refers to a weapon....

 launched with specific initial conditions will have a predictable range. As in Trajectory of a projectile

Trajectory of a projectile

In physics, the ballistic trajectory of a projectile is the path that a thrown or launched projectile will take under the action of gravity, neglecting all other forces, such as friction from air resistance, without propulsion....

, we will use:

The following applies for ranges which are small compared to the size of the Earth. For longer ranges see sub-orbital spaceflight

Sub-orbital spaceflight

A sub-orbital space flight is a spaceflight in which the spacecraft reaches space, but its trajectory intersects the atmosphere or surface of the gravitating body from which it was launched, so that it does not complete one orbital revolution....

.

• g: the gravitational acceleration
  Gravitational acceleration
  In physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
  
  —usually taken to be 9.81 m/s² (32 f/s²) near the Earth's surface
• θ: the angle at which the projectile is launched
• v: the velocity at which the projectile is launched
• y₀: the initial height of the projectile
• d: the total horizontal distance travelled by the projectile

When neglecting air resistance, the range of a projectile will be

If (y₀) is taken to be zero, meaning the object is being launched on flat ground, the range of the projectile will then simplify to

Ideal projectile motion

Ideal projectile motion assumes that there is no air resistance. This assumption simplifies the math greatly, and is a close approximation of actual projectile motion in cases where the distances travelled are small. Ideal projectile motion is also a good introduction to the topic before adding the complications of air resistance.

Flat ground

First we examine the case where (y₀) is zero. The horizontal position of the projectile is

In the vertical direction

We are interested in the time when the projectile returns to the same height it originated at, thus

By factoring:

or

The first solution corresponds to when the projectile is first launched. The second solution is the useful one for determining the range of the projectile. Plugging this value for (t) into the horizontal equation yields

Applying the trigonometric identity

If x and y are same,

allows us to simplify the solution to

Note that when (θ) is 45°, the solution becomes

Uneven ground

Now we will allow (y₀) to be nonzero. Our equations of motion are now

and

Once again we solve for (t) in the case where the (y) position of the projectile is at zero (since this is how we defined our starting height to begin with)

Again by applying the quadratic formula we find two solutions for the time. After several steps of algebraic manipulation

The square root must be a positive number, and since the velocity and the cosine of the launch angle can also be assumed to be positive, the solution with the greater time will occur when the positive of the plus or minus sign is used. Thus, the solution is

Solving for the range once again

Maximum range

For cases where the projectile lands at the same height from which it is launched, the maximum range is obtained by using a launch angle of 45 degrees. A projectile that is launched with an elevation of 0 degrees will strike the ground immediately (range = 0), though it may then bounce or roll. A projectile that is fired with an elevation of 90 degrees (i.e. straight up) will travel straight up, then straight down, and strike the ground at the point from which it is launched, again yielding a range of 0.

The elevation angle which will provide the maximum range when launching the projectile from a non-zero initial height can be computed by finding the derivative of the range with respect to the elevation angle and setting the derivative to zero to find the extremum:

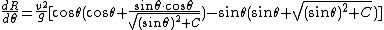
where 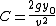and 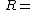horizontal range.

Setting the derivative to zero provides the equation:

Substituting and produces:

Which reduces to the extremely surprisingly simple expression:

Replacing our substitutions yields the angle that produces the maximum range for uneven ground, ignoring air resistance:

Note that for zero initial height, the elevation angle that produces maximum range is 45 degrees, as expected. For positive initial heights, the elevation angle is below 45 degrees, and for negative initial heights (bounded below by 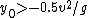), the elevation angle is greater than 45 degrees.

Example: For the values , , 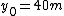and , an elevation angle 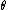= 41.1° produces a maximum range of .

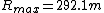Angle of impact

The angle ψ at which the projectile lands is given by:

For maximum range, this results in the following equation:

Rewriting the original solution for θ, we get:

Multiplying with the equation for (tan ψ)^2 gives:

Because of the trigonometric identity

,

this means that θ + ψ must be 90 degrees.

Actual projectile motion

In addition to air resistance, which slows a projectile and reduces its range, many other factors also have to be accounted for when actual projectile motion is considered.

Projectile characteristics

Generally speaking, a projectile with greater volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

 faces greater air resistance, reducing the range of the projectile. This can be modified by the projectile shape: a tall and wide, but short projectile will face greater air resistance than a low and narrow, but long, projectile of the same volume. The surface of the projectile also must be considered: a smooth projectile will face less air resistance than a rough-surfaced one, and irregularities on the surface of a projectile may change its trajectory if they create more drag

Drag (physics)

In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...

 on one side of the projectile than on the other. Mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

 also becomes important, as a more massive projectile will have more kinetic energy

Kinetic energy

The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...

, and will thus be less affected by air resistance. The distribution of mass within the projectile can also be important, as an unevenly weighted projectile may spin undesirably, causing irregularities in its trajectory

Trajectory

A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...

 due to the magnus effect

Magnus effect

The Magnus effect is the phenomenon whereby a spinning object flying in a fluid creates a whirlpool of fluid around itself, and experiences a force perpendicular to the line of motion...

.

If a projectile is given rotation along its axes of travel, irregularities in the projectile's shape and weight distribution tend to be canceled out. See rifling

Rifling

Rifling is the process of making helical grooves in the barrel of a gun or firearm, which imparts a spin to a projectile around its long axis...

 for a greater explanation.

Firearm barrels

For projectiles that are launched by firearms and artillery, the nature of the gun's barrel

Gun barrel

A gun barrel is the tube, usually metal, through which a controlled explosion or rapid expansion of gases are released in order to propel a projectile out of the end at a high velocity....

 is also important. Longer barrels allow more of the propellant

Propellant

A propellant is a material that produces pressurized gas that:* can be directed through a nozzle, thereby producing thrust ;...

's energy to be given to the projectile, yielding greater range. Rifling

Rifling

Rifling is the process of making helical grooves in the barrel of a gun or firearm, which imparts a spin to a projectile around its long axis...

, while it may not increase the average (arithmetic mean

Arithmetic mean

In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...

) range of many shots from the same gun, will increase the accuracy and precision

Accuracy and precision

In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...

of the gun.