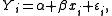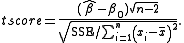Student's t-test
Encyclopedia
A t-test is any statistical hypothesis test
in which the test statistic
follows a Student's t distribution if the null hypothesis
is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known. When the scaling term is unknown and is replaced by an estimate based on the data
, the test statistic (under certain conditions) follows a Student's t distribution.
, a chemist working for the Guinness
brewery
in Dublin, Ireland ("Student" was his pen name
). Gosset had been hired due to Claude Guinness's policy of recruiting the best graduates from Oxford and Cambridge to apply biochemistry
and statistics
to Guinness' industrial processes. Gosset devised the t-test as a way to cheaply monitor the quality of stout
. He published the test in Biometrika
in 1908, but was forced to use a pen name by his employer, who regarded the fact that they were using statistics as a trade secret. In fact, Gosset's identity was known to fellow statisticians.
As an example, in the one-sample t-test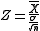
, where 
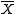is the sample mean
of the data, n is the sample size, and σ is the population standard deviation of the data; s in the one-sample t-test is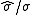
, where 
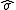is the sample standard deviation.
The assumptions underlying a t-test are that
In a specific type of t-test, these conditions are consequences of the population
being studied, and of the way in which the data are sampled
. For example, in the t-test comparing the means of two independent samples, the following assumptions should be met:
, and have greater power
than unpaired tests when the paired units are similar with respect to "noise factors" that are independent of membership in the two groups being compared. In a different context, paired t-tests can be used to reduce the effects of confounding factors in an observational study
.
The unpaired, or "independent samples" t-test is used when two separate sets of independent and identically distributed samples are obtained, one from each of the two populations being compared. For example, suppose we are evaluating the effect of a medical treatment, and we enroll 100 subjects into our study, then randomize 50 subjects to the treatment group and 50 subjects to the control group. In this case, we have two independent samples and would use the unpaired form of the t-test. The randomization is not essential here—if we contacted 100 people by phone and obtained each person's age and gender, and then used a two-sample t-test to see whether the mean ages differ by gender, this would also be an independent samples t-test, even though the data are observational.
Dependent samples (or "paired") t-tests typically consist of a sample of matched pairs of similar units, or one group of units that has been tested twice (a "repeated measures" t-test). A typical example of the repeated measures t-test would be where subjects are tested prior to a treatment, say for high blood pressure, and the same subjects are tested again after treatment with a blood-pressure lowering medication.
A dependent t-test based on a "matched-pairs sample" results from an unpaired sample that is subsequently used to form a paired sample, by using additional variables that were measured along with the variable of interest. The matching is carried out by identifying pairs of values consisting of one observation from each of the two samples, where the pair is similar in terms of other measured variables. This approach is often used in observational studies to reduce or eliminate the effects of confounding factors.
are given in each case. Each of these statistics can be used to carry out either a one-tailed test or a two-tailed test
.
Once a t value is determined, a p-value
can be found using a table of values from Student's t-distribution. If the calculated p-value is below the threshold chosen for statistical significance
(usually the 0.10, the 0.05, or 0.01 level), then the null hypothesis is rejected in favor of the alternative hypothesis.
where
is the sample mean, s is the sample standard deviation of the sample and n is the sample size. The degrees of freedom used in this test is n − 1.
where xi, i = 1, ..., n are known, α and β are unknown, and εi are independent identically normally distributed random errors
with expected value 0 and unknown variance σ2, and Yi, i = 1, ..., n are observed. It is desired to test the null hypothesis that the slope β is equal to some specified value β0 (often taken to be 0, in which case the hypothesis is that x and y are unrelated).
Let
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
in which the test statistic
Test statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
follows a Student's t distribution if the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known. When the scaling term is unknown and is replaced by an estimate based on the data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
, the test statistic (under certain conditions) follows a Student's t distribution.
History
The t-statistic was introduced in 1908 by William Sealy GossetWilliam Sealy Gosset
William Sealy Gosset is famous as a statistician, best known by his pen name Student and for his work on Student's t-distribution....
, a chemist working for the Guinness
Guinness
Guinness is a popular Irish dry stout that originated in the brewery of Arthur Guinness at St. James's Gate, Dublin. Guinness is directly descended from the porter style that originated in London in the early 18th century and is one of the most successful beer brands worldwide, brewed in almost...
brewery
Brewery
A brewery is a dedicated building for the making of beer, though beer can be made at home, and has been for much of beer's history. A company which makes beer is called either a brewery or a brewing company....
in Dublin, Ireland ("Student" was his pen name
Pen name
A pen name, nom de plume, or literary double, is a pseudonym adopted by an author. A pen name may be used to make the author's name more distinctive, to disguise his or her gender, to distance an author from some or all of his or her works, to protect the author from retribution for his or her...
). Gosset had been hired due to Claude Guinness's policy of recruiting the best graduates from Oxford and Cambridge to apply biochemistry
Biochemistry
Biochemistry, sometimes called biological chemistry, is the study of chemical processes in living organisms, including, but not limited to, living matter. Biochemistry governs all living organisms and living processes...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
to Guinness' industrial processes. Gosset devised the t-test as a way to cheaply monitor the quality of stout
Stout
Stout is a dark beer made using roasted malt or barley, hops, water and yeast. Stouts were traditionally the generic term for the strongest or stoutest porters, typically 7% or 8%, produced by a brewery....
. He published the test in Biometrika
Biometrika
- External links :* . The Internet Archive. 2011....
in 1908, but was forced to use a pen name by his employer, who regarded the fact that they were using statistics as a trade secret. In fact, Gosset's identity was known to fellow statisticians.
Uses
Among the most frequently used t-tests are:- A one-sample location testLocation testA location test is a statistical hypothesis test that compares the location parameter of a statistical population to a given constant, or that compares the location parameters of two statistical populations to each other...
of whether the mean of a normally distributed population has a value specified in a null hypothesisNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
.
- A two sample location test of the null hypothesis that the meanExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s of two normally distributed populations are equal. All such tests are usually called Student's t-tests, though strictly speaking that name should only be used if the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s of the two populations are also assumed to be equal; the form of the test used when this assumption is dropped is sometimes called Welch's t-testWelch's t testIn statistics, Welch's t test is an adaptation of Student's t-test intended for use with two samples having possibly unequal variances. As such, it is an approximate solution to the Behrens–Fisher problem.-Formulas:...
. These tests are often referred to as "unpaired" or "independent samples" t-tests, as they are typically applied when the statistical units underlying the two samples being compared are non-overlapping.
- A test of the null hypothesis that the difference between two responses measured on the same statistical unit has a mean value of zero. For example, suppose we measure the size of a cancer patient's tumor before and after a treatment. If the treatment is effective, we expect the tumor size for many of the patients to be smaller following the treatment. This is often referred to as the "paired" or "repeated measures" t-test: see paired difference testPaired difference testIn statistics, a paired difference test is a type of location test that is used when comparing two sets of measurements to assess whether their population means differ...
.
- A test of whether the slope of a regression lineLinear regressionIn statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
differs significantlyStatistical significanceIn statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
from 0.
Assumptions
Most t-test statistics have the form T = Z/s, where Z and s are functions of the data. Typically, Z is designed to be sensitive to the alternative hypothesis (i.e. its magnitude tends to be larger when the alternative hypothesis is true), whereas s is a scaling parameter that allows the distribution of T to be determined.As an example, in the one-sample t-test
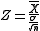, where 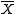is the sample meanAverage
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
of the data, n is the sample size, and σ is the population standard deviation of the data; s in the one-sample t-test is
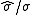, where 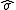is the sample standard deviation.The assumptions underlying a t-test are that
- Z follows a standard normal distribution under the null hypothesis
- ps2 follows a χ2 distribution with p degrees of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
under the null hypothesis, where p is a positive constant - Z and s are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
.
In a specific type of t-test, these conditions are consequences of the population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
being studied, and of the way in which the data are sampled
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
. For example, in the t-test comparing the means of two independent samples, the following assumptions should be met:
- Each of the two populations being compared should follow a normal distribution. This can be tested using a normality testNormality testIn statistics, normality tests are used to determine whether a data set is well-modeled by a normal distribution or not, or to compute how likely an underlying random variable is to be normally distributed....
, such as the Shapiro-Wilk or Kolmogorov–Smirnov test, or it can be assessed graphically using a normal quantile plotQ-Q plotIn statistics, a Q-Q plot is a probability plot, which is a graphical method for comparing two probability distributions by plotting their quantiles against each other. First, the set of intervals for the quantiles are chosen...
.
- If using Student's original definition of the t-test, the two populations being compared should have the same variance (testable using Levene's testLevene's testIn statistics, Levene's test is an inferential statistic used to assess the equality of variances in different samples. Some common statistical procedures assume that variances of the populations from which different samples are drawn are equal. Levene's test assesses this assumption. It tests the...
, Bartlett's testBartlett's testIn statistics, Bartlett's test is used to test if k samples are from populations with equal variances. Equal variances across samples is called homoscedasticity or homogeneity of variances. Some statistical tests, for example the analysis of variance, assume that variances are equal across groups...
, or the Brown–Forsythe test; or assessable graphically using a normal quantile plotQ-Q plotIn statistics, a Q-Q plot is a probability plot, which is a graphical method for comparing two probability distributions by plotting their quantiles against each other. First, the set of intervals for the quantiles are chosen...
). If the sample sizes in the two groups being compared are roughly equal, Student's original t-test is highly robust to the presence of unequal variances. Welch's t-test is insensitive to equality of the variances regardless of whether the sample sizes are similar. - The data used to carry out the test should be sampled independently from the two populations being compared. This is in general not testable from the data, but if the data are known to be dependently sampled (i.e. if they were sampled in clusters), then the classical t-tests discussed here may give misleading results.
Unpaired and paired two-sample t-tests
Two-sample t-tests for a difference in mean can be either unpaired or paired. Paired t-tests are a form of blockingBlocking (statistics)
In the statistical theory of the design of experiments, blocking is the arranging of experimental units in groups that are similar to one another. For example, an experiment is designed to test a new drug on patients. There are two levels of the treatment, drug, and placebo, administered to male...
, and have greater power
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
than unpaired tests when the paired units are similar with respect to "noise factors" that are independent of membership in the two groups being compared. In a different context, paired t-tests can be used to reduce the effects of confounding factors in an observational study
Observational study
In epidemiology and statistics, an observational study draws inferences about the possible effect of a treatment on subjects, where the assignment of subjects into a treated group versus a control group is outside the control of the investigator...
.
The unpaired, or "independent samples" t-test is used when two separate sets of independent and identically distributed samples are obtained, one from each of the two populations being compared. For example, suppose we are evaluating the effect of a medical treatment, and we enroll 100 subjects into our study, then randomize 50 subjects to the treatment group and 50 subjects to the control group. In this case, we have two independent samples and would use the unpaired form of the t-test. The randomization is not essential here—if we contacted 100 people by phone and obtained each person's age and gender, and then used a two-sample t-test to see whether the mean ages differ by gender, this would also be an independent samples t-test, even though the data are observational.
Dependent samples (or "paired") t-tests typically consist of a sample of matched pairs of similar units, or one group of units that has been tested twice (a "repeated measures" t-test). A typical example of the repeated measures t-test would be where subjects are tested prior to a treatment, say for high blood pressure, and the same subjects are tested again after treatment with a blood-pressure lowering medication.
A dependent t-test based on a "matched-pairs sample" results from an unpaired sample that is subsequently used to form a paired sample, by using additional variables that were measured along with the variable of interest. The matching is carried out by identifying pairs of values consisting of one observation from each of the two samples, where the pair is similar in terms of other measured variables. This approach is often used in observational studies to reduce or eliminate the effects of confounding factors.
Calculations
Explicit expressions that can be used to carry out various t-tests are given below. In each case, the formula for a test statistic that either exactly follows or closely approximates a t-distribution under the null hypothesis is given. Also, the appropriate degrees of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
are given in each case. Each of these statistics can be used to carry out either a one-tailed test or a two-tailed test
Two-tailed test
The two-tailed test is a statistical test used in inference, in which a given statistical hypothesis, H0 , will be rejected when the value of the test statistic is either sufficiently small or sufficiently large...
.
Once a t value is determined, a p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
can be found using a table of values from Student's t-distribution. If the calculated p-value is below the threshold chosen for statistical significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
(usually the 0.10, the 0.05, or 0.01 level), then the null hypothesis is rejected in favor of the alternative hypothesis.
One-sample t-test
In testing the null hypothesis that the population mean is equal to a specified value μ0, one uses the statisticwhere
is the sample mean, s is the sample standard deviation of the sample and n is the sample size. The degrees of freedom used in this test is n − 1.Slope of a regression line
Suppose one is fitting the model
where xi, i = 1, ..., n are known, α and β are unknown, and εi are independent identically normally distributed random errors
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
with expected value 0 and unknown variance σ2, and Yi, i = 1, ..., n are observed. It is desired to test the null hypothesis that the slope β is equal to some specified value β0 (often taken to be 0, in which case the hypothesis is that x and y are unrelated).
Let
-
Then
-
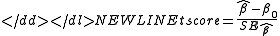
has a t-distribution with n − 2 degrees of freedom if the null hypothesis is true.
The standard error of the angular coefficient:
-
can be written in terms of the residuals. Let
-
Then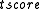
is given by:
Equal sample sizes, equal variance
This test is only used when both:- the two sample sizes (that is, the number, n, of participants of each group) are equal;
- it can be assumed that the two distributions have the same variance.
Violations of these assumptions are discussed below.
The t statistic to test whether the means are different can be calculated as follows: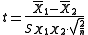
where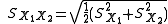
Here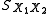
is the grand standard deviation (or pooled standard deviation), 1 = group one, 2 = group two. The denominator of t is the standard errorStandard error (statistics)The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
of the difference between two means.
For significance testing, the degrees of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
for this test is 2n − 2 where n is the number of participants in each group.
Unequal sample sizes, equal variance
This test is used only when it can be assumed that the two distributions have the same variance. (When this assumption is violated, see below.) The t statistic to test whether the means are different can be calculated as follows: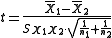
where
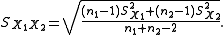
Note that the formulae above are generalizations of the case where both samples have equal sizes (substitute n for n1 and n2).
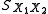is an estimator of the common standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the two samples: it is defined in this way so that its square is an unbiased estimator of the common variance whether or not the population means are the same. In these formulae, n = number of participants, 1 = group one, 2 = group two. n − 1 is the number of degrees of freedom for either group, and the total sample size minus two (that is, n1 + n2 − 2) is the total number of degrees of freedom, which is used in significance testing.
Unequal sample sizes, unequal variance
This test also known as Welch's t-testWelch's t testIn statistics, Welch's t test is an adaptation of Student's t-test intended for use with two samples having possibly unequal variances. As such, it is an approximate solution to the Behrens–Fisher problem.-Formulas:...
is used only when the two population variances are assumed to be different (the two sample sizes may or may not be equal) and hence must be estimated separately. The t statistic to test whether the population means are different can be calculated as follows:
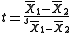
where
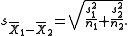
Where s2 is the unbiased estimator of the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the two samples, n = number of participants, 1 = group one, 2 = group two. Note that in this case,
is not a pooled variance. For use in significance testing, the distribution of the test statistic is approximated as being an ordinary Student's t distribution with the degrees of freedom calculated using
This is called the Welch–Satterthwaite equation. Note that the true distribution of the test statistic actually depends (slightly) on the two unknown variances: see Behrens–Fisher problem.
Dependent t-test for paired samples
This test is used when the samples are dependent; that is, when there is only one sample that has been tested twice (repeated measures) or when there are two samples that have been matched or "paired". This is an example of a paired difference testPaired difference testIn statistics, a paired difference test is a type of location test that is used when comparing two sets of measurements to assess whether their population means differ...
.
For this equation, the differences between all pairs must be calculated. The pairs are either one person's pre-test and post-test scores or between pairs of persons matched into meaningful groups (for instance drawn from the same family or age group: see table). The average (XD) and standard deviation (sD) of those differences are used in the equation. The constant μ0 is non-zero if you want to test whether the average of the difference is significantly different from μ0. The degree of freedom used is n − 1.Example of repeated measures Number Name Test 1 Test 2 1 Mike 35% 67% 2 Melanie 50% 46% 3 Melissa 90% 86% 4 Mitchell 78% 91% Example of matched pairs Pair Name Age Test 1 John 35 250 1 Jane 36 340 2 Jimmy 22 460 2 Jessy 21 200
Worked examples
Let A1 denote a set obtained by taking 6 random samples out of a larger set:
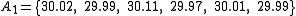
and let A2 denote a second set obtained similarly:
These could be, for example, the weights of screws that were chosen out of a bucket.
We will carry out tests of the null hypothesis that the meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
s of the populations from which the two samples were taken are equal.
The difference between the two sample means, each denoted by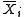
, which appears in the numerator for all the two-sample testing approaches discussed above, is
The sample standard deviations for the two samples are approximately 0.05 and 0.11, respectively. For such small samples, a test of equality between the two population variances would not be very powerful. Since the sample sizes are equal, the two forms of the two sample t-test will perform similarly in this example.
Unequal variances
If the approach for unequal variances (discussed above) is followed, the results are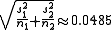
and
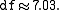
The test statistic is approximately 1.959. The two-tailed testTwo-tailed testThe two-tailed test is a statistical test used in inference, in which a given statistical hypothesis, H0 , will be rejected when the value of the test statistic is either sufficiently small or sufficiently large...
p-valueP-valueIn statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
is approximately 0.091 and the one-tailed p-value is approximately 0.045.
Equal variances
If the approach for equal variances (discussed above) is followed, the results are
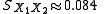
and
Since the sample sizes are equal (both are 6), the test statistic is again approximately equal to 1.959. Since the degrees of freedom is different from what it is in the unequal variances test, the p-values will differ slightly from what was found above. Here, the two-tailed p-value is approximately 0.078, and the one-tailed p-value is approximately 0.039. Thus if there is good reason to believe that the population variances are equal, the results become somewhat more suggestive of a difference in the mean weights for the two populations of screws.
Alternatives to the t-test for location problems
The t-test provides an exact test for the equality of the means of two normal populations with unknown, but equal, variances. (The Welch's t-test is a nearly-exact test for the case where the data are normal but the variances may differ.) For moderately large samples and a one tailed test, the t is relatively robust to moderate violations of the normality assumption.
For exactness, the t-test and Z-test require normality of the sample means, and the t-test additionally requires that the sample variance follows a scaled χ2 distribution, and that the sample mean and sample variance be statistically independent. Normality of the individual data values is not required if these conditions are met. By the central limit theoremCentral limit theoremIn probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, sample means of moderately large samples are often well-approximated by a normal distribution even if the data are not normally distributed. For non-normal data, the distribution of the sample variance may deviate substantially from a χ2 distribution. However, if the sample size is large, Slutsky's theoremSlutsky's theoremIn probability theory, Slutsky’s theorem extends some properties of algebraic operations on convergent sequences of real numbers to sequences of random variables.The theorem was named after Eugen Slutsky. Slutsky’s theorem is also attributed to Harald Cramér....
implies that the distribution of the sample variance has little effect on the distribution of the test statistic. If the data are substantially non-normal and the sample size is small, the t-test can give misleading results. See Location test for Gaussian scale mixture distributionsLocation testing for Gaussian scale mixture distributionsIn statistics, the topic of location testing for Gaussian scale mixture distributions arises in some particular types of situations where the more standard Student's t-test is inapplicable...
for some theory related to one particular family of non-normal distributions.
When the normality assumption does not hold, a non-parametric alternative to the t-test can often have better statistical powerStatistical powerThe power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
. For example, for two independent samples when the data distributions are asymmetric (that is, the distributions are skewedSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
) or the distributions have large tails, then the Wilcoxon Rank Sum test (also known as the Mann-Whitney U test) can have three to four times higher power than the t-test. The nonparametric counterpart to the paired samples t test is the Wilcoxon signed-rank testWilcoxon signed-rank testThe Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used when comparing two related samples or repeated measurements on a single sample to assess whether their population mean ranks differ The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used...
for paired samples. For a discussion on choosing between the t and nonparametric alternatives, see Sawilowsky.
One-way analysis of varianceAnalysis of varianceIn statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
generalizes the two-sample t-test when the data belong to more than two groups.
Multivariate testing
A generalization of Student's t statistic, called Hotelling's T-square statistic, allows for the testing of hypotheses on multiple (often correlated) measures within the same sample. For instance, a researcher might submit a number of subjects to a personality test consisting of multiple personality scales (e.g. the Big FiveBig Five personality traitsIn contemporary psychology, the "Big Five" factors of personality are five broad domains or dimensions of personality which are used to describe human personality....
). Because measures of this type are usually highly correlated, it is not advisable to conduct separate univariate t-tests to test hypotheses, as these would neglect the covariance among measures and inflate the chance of falsely rejecting at least one hypothesis (Type I error). In this case a single multivariate test is preferable for hypothesis testing. Hotelling's T 2 statistic follows a T 2 distribution. However, in practice the distribution is rarely used, and instead converted to an F distribution.
One-sample T 2 test
For a one-sample multivariate test, the hypothesis is that the mean vector (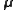
) is equal to a given vector (
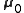). The test statistic is defined as:
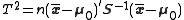
where n is the sample size,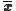
is the vector of column means and 
is a 
sample covariance matrix.
Two-sample T 2 test
For a two-sample multivariate test, the hypothesis is that the mean vector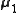s (
, 
) of two samples are equal. The test statistic is defined as
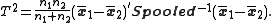
Implementations
Most spreadsheetSpreadsheetA spreadsheet is a computer application that simulates a paper accounting worksheet. It displays multiple cells usually in a two-dimensional matrix or grid consisting of rows and columns. Each cell contains alphanumeric text, numeric values or formulas...
programs and statistics packages, such as QtiPlotQtiPlotQtiPlot is a platform-independent open-source cross-platform computer program for interactive scientific graphing and data analysis. It is similar to the proprietary programs Origin or SigmaPlot, and is being used to substitute these in universities ....
, OpenOffice.org CalcOpenOffice.org CalcOpenOffice.org Calc is the spreadsheet component of the OpenOffice.org software package.Calc is similar to Microsoft Excel, with a roughly equivalent range of features. Calc is capable of opening and saving most spreadsheets in Microsoft Excel file format...
, Microsoft ExcelMicrosoft ExcelMicrosoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
, SAS, SPSSSPSSSPSS is a computer program used for survey authoring and deployment , data mining , text analytics, statistical analysis, and collaboration and deployment ....
, StataStataStata is a general-purpose statistical software package created in 1985 by StataCorp. It is used by many businesses and academic institutions around the world...
, DAPDAP (software)Dap is a statistics and graphics program, that performs data management, analysis, and graphical visualization tasks which are commonly required in statistical consulting practice....
, gretlGretlgretl is an open-source statistical package, mainly for econometrics. The name is an acronym for Gnu Regression, Econometrics and Time-series Library. It has a graphical user interface and can be used together with X-12-ARIMA, TRAMO/SEATS, R, Octave, and Ox. It is written in C, uses GTK as widget...
, RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
, PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
(http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html), PSPPPSPPPSPP is a free software application for analysis of sampled data. It has a graphical user interface and conventional command line interface. It is written in C, uses GNU Scientific Library for its mathematical routines, and plotutils for generating graphs....
, and Minitab, include implementations of Student's t-test.
See also
- Student's t-statisticStudent's t-statisticIn statistics, the t-statistic is a ratio of the departure of an estimated parameter from its notional value and its standard error. It is used in hypothesis testing, for example in the Student's t-test, in the augmented Dickey–Fuller test, and in bootstrapping.-Definition:Let \scriptstyle\hat\beta...
- F-testF-testAn F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
- Conditional change modelConditional change modelThe conditional change model in statistics is the analytic procedure in which change scores are regressed on baseline values, together with the explanatory variables of interest . The method has some substantial advantages over the usual two-sample t-test recommended in textbooks.-References:*...
External links
Online calculators
-
-
-
-
