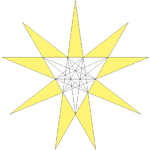
Final stellation of the icosahedron
Encyclopedia
| Final stellation of the icosahedron | |||||||
|---|---|---|---|---|---|---|---|
Two symmetric orthographic projection Orthographic projection Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface... s |
|||||||
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation... (Ih) |
||||||
| Type | Stellated icosahedron, 8th of 59 | ||||||
| Symbols | Du Val H Wenninger: W42 |
||||||
| Elements Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... (As a star polyhedron) |
F = 20, E = 90 V = 60 (χ = −10) |
||||||
| Elements Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... (As a simple polyhedron) |
F = 180, E = 270, V = 92 (χ = 2) |
||||||
| Properties (As a star polyhedron) |
Vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... , face-transitive |
||||||
|
|||||||
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the complete or final stellation of the icosahedron is the outermost stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
of the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram
Stellation diagram
In geometry, a stellation diagram or stellation pattern is a two-dimensional diagram in the plane of some face of a polyhedron, showing lines where other face planes intersect with this one. The lines cause 2D space to be divided up into regions. Regions not intersected by any further lines are...
.
It is also called the echidnahedron. This polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
is the seventeenth stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
of the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, and given as Wenninger model index 42.
As a geometrical figure, it has two interpretations, described below:
- As an irregularRegular polyhedronA regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
star (self-intersecting) polyhedron with 20 identical self-intersecting star polygon faces, 90 edge, 60 vertices. - As a simple polyhedron with 180 triangular faces (60 isosceles, 120 scalene), 270 edges, and 92 vertices. This interpretation is useful for polyhedron modelPolyhedron modelA polyhedron model is a physical construction of a polyhedron, constructed from cardboard, plastic board, wood board or other panel material, or, less commonly, solid material....
building.
Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
researched stellations that create regular star polyhedra (the Kepler-Poinsot polyhedra) in 1619, but the complete icosahedron, with irregular faces, was first studied in 1900 by Max Brückner.
History

- 1619: In Harmonices Mundi, Johannes KeplerJohannes KeplerJohannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
first applied the stellation process, recognizing the small stellated dodecahedron and great stellated dodecahedron as regular polyhedra. - 1809: Louis PoinsotLouis PoinsotLouis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...
rediscovered Kepler's polyhedra and two more, the great icosahedron and great dodecahedron as regular star polyhedra, now called the Kepler–Poinsot polyhedra. - 1812: Augustin-Louis Cauchy made a further enumeration of star polyhedra, proving there are only 4 regular star polyhedra.
- 1900: Max Brückner extended the stellation theory beyond regular forms, and identified ten stellations of the icosahedron, including the complete stellation.
- 1924: A.H. Wheeler in 1924 published a list of 20 stellation forms (22 including reflective copies), also including the complete stellation.
- 1938: In their 1938 book The Fifty Nine IcosahedraThe fifty nine icosahedraThe Fifty Nine Icosahedra is a book written and illustrated by H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates the stellations of the regular convex or Platonic icosahedron, according to a set of rules put forward by J. C. P. Miller...
, H. S. M. CoxeterHarold Scott MacDonald CoxeterHarold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....
, P. Du ValPatrick du ValPatrick du Val was a British mathematician, known for his work on algebraic geometry, differential geometry, and general relativity. The concept of Du Val singularity of an algebraic surface is named after him....
, H. T. Flather and J. F. Petrie stated a set of stellation rules for the regular icosahedron and gave a systematic enumeration of the fifty-nine stellations which conform to those rules. The complete stellation is referenced as the eighth in the book. - 1974: In WenningerMagnus WenningerFather Magnus J. Wenninger OSB is a mathematician who works on constructing polyhedron models, and wrote the first book on their construction.-Early life and education:...
's 1974 book Polyhedron Models, the final stellation of the icosahedron is included as the 17th model of stellated icosahedra with index number W42. - 1995: Andrew Hume named it in his NetlibNetlibNetlib is a repository of software for scientific computing maintained by AT&T, Bell Laboratories, the University of Tennessee and Oak Ridge National Laboratory. Netlib comprises a large number of separate programs and libraries...
polyhedral database as the echidnahedron (the echidnaEchidnaEchidnas , also known as spiny anteaters, belong to the family Tachyglossidae in the monotreme order of egg-laying mammals. There are four extant species, which, together with the platypus, are the only surviving members of that order and are the only extant mammals that lay eggs...
, or spiny anteater, is a small mammalMammalMammals are members of a class of air-breathing vertebrate animals characterised by the possession of endothermy, hair, three middle ear bones, and mammary glands functional in mothers with young...
that is covered with coarse hairHairHair is a filamentous biomaterial, that grows from follicles found in the dermis. Found exclusively in mammals, hair is one of the defining characteristics of the mammalian class....
and spinesSpine (zoology)A spine is a hard, thorny or needle-like structure which occurs on various animals. Animals such as porcupines and sea urchins grow spines as a self-defense mechanism. Spines are often formed of keratin...
).
Interpretations
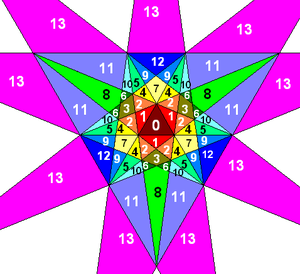
As a stellation
The stellationStellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
of a polyhedron extends the faces of a polyhedron into infinite planes and generates a new polyhedron that is bounded by these planes as faces and the intersections of these planes as edges. The Fifty Nine Icosahedra enumerates the stellations of the regular icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, according to a set of rules put forward by J. C. P. Miller
J. C. P. Miller
Jeffrey Charles Percy Miller was an English mathematician and computing pioneer. He worked in number theory and on geometry, particularly polyhedra, where Miller's monster refers to the great dirhombicosidodecahedron....
, including the complete stellation. The Du Val symbol of the complete stellation is H, because it includes all cells in the stellation diagram up to and including the outermost "h" layer.
As a simple polyhedron
A polyhedral model can be constructed by 12 sets of faces, each folded into a group of five pyramids. |
As a simple, visible surface polyhedron, the outward form of the final stellation is composed of 180 triangular faces, which are the outermost triangular regions in the stellation diagram. These join along 270 edges, which in turn meet at 92 vertices, with an Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of 2.
The 92 vertices lie on the surfaces of three concentric spheres. The innermost group of 20 vertices form the vertices of a regular dodecahedron; the next layer of 12 form the vertices of a regular icosahedron; and the outer layer of 60 form the vertices of a nonuniform truncated icosahedron. The radii of these spheres are in the ratio

| Inner | Middle | Outer | All three |
|---|---|---|---|
| 20 vertices | 12 vertices | 60 vertices | 92 vertices |
 Dodecahedron |
 Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
Nonuniform truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
Complete icosahedron |
When regarded as a three-dimensional solid object with edge lengths a, φa, φ2a and φ2a√2 (where φ is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
) the complete icosahedron has surface area
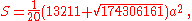
and volume

As a star polyhedron
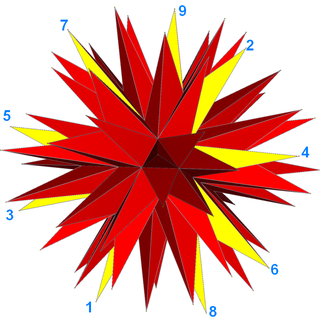 Twenty (9/4) polygon faces (one face is drawn yellow with 9 vertices labeled.) |
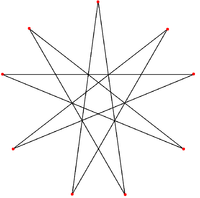 2-isogonal (9/4) faces |
The complete stellation can also be seen as a self-intersecting star polyhedron
Star polyhedron
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
having 20 faces corresponding to the 20 faces of the underlying icosahedron. Each face is an irregular 9/4 star polygon, or enneagram
Enneagram (geometry)
In geometry, an enneagram is a nine-pointed geometric figure. It is sometimes called a nonagram.-Regular enneagram:A regular enneagram is constructed using the same points as the regular enneagon but connected in fixed steps...
. Since three faces meet at each vertex it has 20 × 9 / 3 = 60 vertices (these are the outermost layer of visible vertices and form the tips of the "spines") and 20 × 9 / 2 = 90 edges (each edge of the star polyhedron includes and connects two of the 180 visible edges).
When regarded as a star icosahedron, the complete stellation is a noble polyhedron
Noble polyhedron
A noble polyhedron is one which is isohedral and isogonal . They were first studied in any depth by Hess and Bruckner around the turn of the century , and later by Grünbaum.-Classes of noble polyhedra:...
, because it is both isohedral (face-transitive) and isogonal (vertex-transitive).
External links
- With instructions for constructing a model of the echidnahedron (.docMicrosoft WordMicrosoft Word is a word processor designed by Microsoft. It was first released in 1983 under the name Multi-Tool Word for Xenix systems. Subsequent versions were later written for several other platforms including IBM PCs running DOS , the Apple Macintosh , the AT&T Unix PC , Atari ST , SCO UNIX,...
) by Ralph Jones - Towards stellating the icosahedron and faceting the dodecahedron by Guy Inchbald
}
- Stellations of the icosahedron
- 59 Stellations of the Icosahedron
- VRMLVRMLVRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind...
model: http://www.georgehart.com/virtual-polyhedra/vrml/echidnahedron.wrl - NetlibNetlibNetlib is a repository of software for scientific computing maintained by AT&T, Bell Laboratories, the University of Tennessee and Oak Ridge National Laboratory. Netlib comprises a large number of separate programs and libraries...
: Polyhedron database, model 141