First fundamental form
Encyclopedia
In differential geometry, the first fundamental form is the inner product on the tangent space
of a surface
in three-dimensional Euclidean space
which is induced canonically from the dot product
of R3. It permits the calculation of curvature
and metric properties of a surface such as length and area in a manner consistent with the ambient space
. The first fundamental form is denoted by the Roman numeral I,
Let X(u, v) be a parametric surface
. Then the inner product of two tangent vector
s is
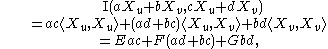
where E, F, and G are the coefficients of the first fundamental form.
The first fundamental form may be represented as a symmetric matrix.
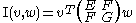
The first fundamental form is often written in the modern notation of the metric tensor
. The coefficients may then be written as
:
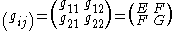
The components of this tensor are calculated as the scalar product of tangent vectors X1 and X2:
for i, j = 1, 2. See example below.
ds may be expressed in terms of the coefficients of the first fundamental form as
.
The classical area element given by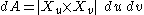
can be expressed in terms of the first fundamental form with the assistance of Lagrange's identity,
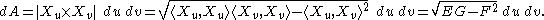
in R3 may be parametrized as
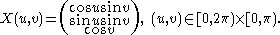
Differentiating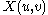
with respect to u and v yields
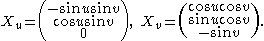
The coefficients of the first fundamental form may be found by taking the dot product of the partial derivatives.
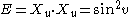
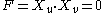
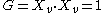
of the sphere is a parametrized curve given by
with t ranging from 0 to 
. The line element may be used to calculate the length of this curve.
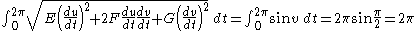
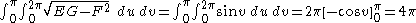
of a surface is given by
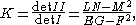
where L, M, and N are the coefficients of the second fundamental form.
Theorema egregium
of Gauss
states that the Gaussian curvature of a surface can be expressed solely in terms of the first fundamental form and its derivatives, so that K is in fact an intrinsic invariant of the surface. An explicit expression for the Gaussian curvature in terms of the first fundamental form is provided by the Brioschi formula.
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
in three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
which is induced canonically from the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of R3. It permits the calculation of curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
and metric properties of a surface such as length and area in a manner consistent with the ambient space
Ambient space
An ambient space, ambient configuration space, or electroambient space, is the space surrounding an object.-Mathematics:In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object...
. The first fundamental form is denoted by the Roman numeral I,
Let X(u, v) be a parametric surface
Parametric surface
A parametric surface is a surface in the Euclidean space R3 which is defined by a parametric equation with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence...
. Then the inner product of two tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s is
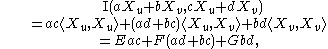
where E, F, and G are the coefficients of the first fundamental form.
The first fundamental form may be represented as a symmetric matrix.
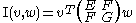
Further notation
When the first fundamental form is written with only one argument, it denotes the inner product of that vector with itself.The first fundamental form is often written in the modern notation of the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. The coefficients may then be written as
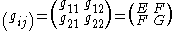
:The components of this tensor are calculated as the scalar product of tangent vectors X1 and X2:
for i, j = 1, 2. See example below.
Calculating lengths and areas
The first fundamental form completely describes the metric properties of a surface. Thus, it enables one to calculate the lengths of curves on the surface and the areas of regions on the surface. The line elementLine element
A line element ds in mathematics can most generally be thought of as the change in a position vector in an affine space expressing the change of the arc length. An easy way of visualizing this relationship is by parametrizing the given curve by Frenet–Serret formulas...
ds may be expressed in terms of the coefficients of the first fundamental form as
. The classical area element given by
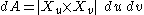can be expressed in terms of the first fundamental form with the assistance of Lagrange's identity,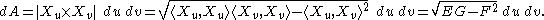Example
The unit sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in R3 may be parametrized as
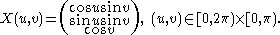
Differentiating
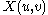with respect to u and v yields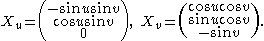The coefficients of the first fundamental form may be found by taking the dot product of the partial derivatives.
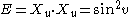
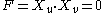
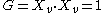
Length of a curve on the sphere
The equatorEquator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
of the sphere is a parametrized curve given by
with t ranging from 0 to . The line element may be used to calculate the length of this curve.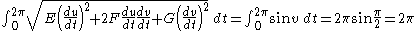Area of a region on the sphere
The area element may be used to calculate the area of the sphere.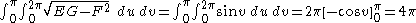Gaussian curvature
The Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
of a surface is given by
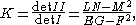
where L, M, and N are the coefficients of the second fundamental form.
Theorema egregium
Theorema Egregium
Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...
of Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
states that the Gaussian curvature of a surface can be expressed solely in terms of the first fundamental form and its derivatives, so that K is in fact an intrinsic invariant of the surface. An explicit expression for the Gaussian curvature in terms of the first fundamental form is provided by the Brioschi formula.